Лабораторная работа э3 Цифровая обработка сигналов

Работа включает:

1.Изучение принципов действия цифровых нерекурсивных фильтров, формирователей ортогональных составляющих (ФОС).

2. Определение разностного уравнения, передаточной функции, алгоритма работы и схемы реализации заданных элементов.

3. Расчет переходных и амплитудно-частотных характеристик.

4. Изучение алгоритма фильтра Фурье

5. Компьютерное исследование цифровых элементов.

Составление предварительного отчета

Методические указания.

1.Изучить основные сведения о программе Simulink (пакет

MATLAB) и характеристики используемых элементов.

Используемые элементы библиотеки Simulink:

Signal Routing – Мультиплексор (смеситель) Mux;

Math Operations– блоки математических операций: блок вычисления суммы Sum, блок умножения Product, усилители Gain, блок вычисления математических функций Math Function;

Continuous – аналоговые блоки: блок фиксированной задержки сигнала Transport Delay;

Sinks-приемники сигналов: осциллограф Scope;

Sources - источники сигналов: генератор ступенчатого сигнала Step, источник синусоидального сигнала Sine Wave;

SimPowerSystems – Extra Library – Discrete Measurements – Discrete Fourier.

Табл.3.1

№	T, с	Порядок ФНЧ	Заданный тип ФОС	Определение ФОС
1	0.02/12	3	1	1.Us = 2. 3. Us = 4. Us =
2	0.02/20	4	2
3	0.02/24	5	3
4	0.02/40	6	4
5	0.02/48	7	1
6	0.02/12	8	2
7	0.02/20	3	3
8	0.02/24	4	4
9	0.02/40	5	1
10	0.02/48	6	2
11	0.02/12	7	3
12	0.02/20	8	4
13	0.02/24	3	1
14	0.02/40	4	2
15	0.02/48	5	3
16	0.02/12	6	4
17	0.02/20	7	1
18	0.02/24	8	2
19	0.02/40	3	3
20	0.02/48	4	4
21	0.02/12	5	1
22	0.02/20	6	2
23	0.02/24	7	3
24	0.02/40	8	4
25	0.02/48	3	1
26	0.02/12	4	2
27	0.02/20	5	3
28	0.02/24	6	4
29	0.02/40	7	1
30	0.02/48	8	2

К п.2. Записать разностное уравнение нерекурсивного фильтра заданного порядка, используя общий вид уравнения простейшего фильтра с единичными коэффициентами:

Хвых[nT]=Хвх[nT] + Хвх[(n-1)T]+…+ Хвх[(n-NT],

где N – заданный порядок фильтра, Т – интервал дискретизации.

По разностному уравнению изображается алгоритм работы фильтра (рис.3.1).

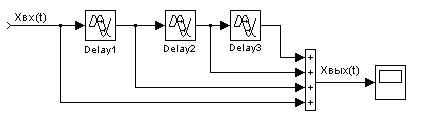
Рис.3.1.Алгоритм нерекурсивного фильтра 3-го порядка.

Передаточная функция данного фильтра в общем виде записывается, как:

H(z)=1+z^-1+z^-2+…+z^-N.

При подстановке в передаточную функцию z=exp(jωT) формируется комплексная частотная характеристика H(jω), модуль которой является амплитудно-частотной характеристикой (АЧХ) H(ω).

, для четных N,

, для нечетных N.

На рис.3.2 в качестве формирователя ортогональной составляющей U_c (Subsystem) использовать заданную схему ФОС. Схема вычисления амплитуды с использованием ортогональных составляющих формируется по формуле

, где U_s, U_c синусная и косинусная составляющие комплексного сигнала.

Рис. 3.2. Схема вычисления амплитуды.

К п.3. Переходная характеристика строится по разностному уравнению при подаче на вход единичного скачка. АЧХ строится в диапазоне частот 0÷2π/Т. При построении АЧХ использовать вспомогательные программы, типа Mathcad, Simulink (Matlab). По характеристике определить частоту, на которой наблюдается первый ноль ω_0,1 , значение H(ω_пр). В схеме рис.3.2 в усилитель поставить коэффициент, обратный значению H(ω_пр).

К п.4. АЧХ фильтра Фурье описывается формулой [5]

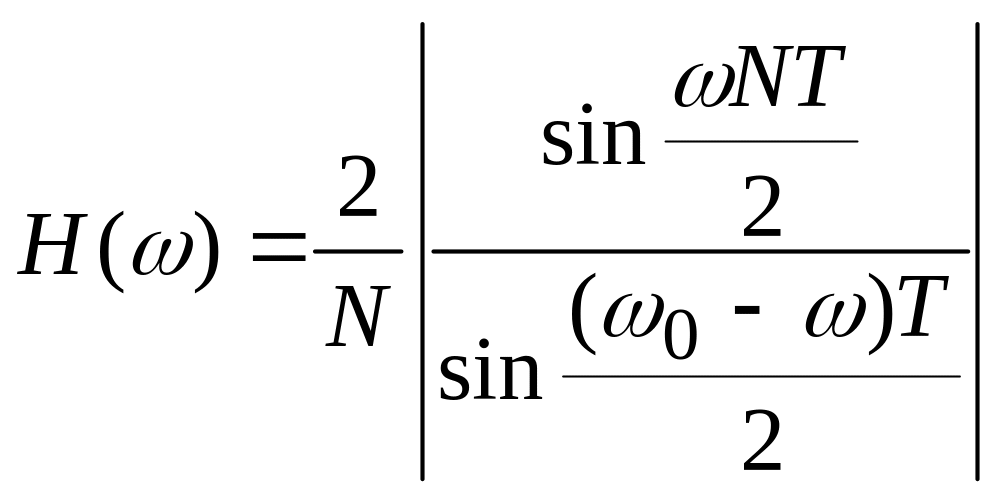, здесь T – интервал дискретизации, – количество выборок на период основной частоты.

Построить зависимость H(ω) в диапазоне частот 0÷2π/Т. При построении АЧХ использовать вспомогательные программы, типа Mathcad, Simulink (Matlab). Определить значение коэффициента преобразования на частоте ω_пр и количество нулей АЧХ.

Работа в лаборатории

При исследовании цифровых элементов не учитываются особенности цифровой обработки, связанные с квантованием по уровню, т.е. работой АЦП. Исследуется основная особенность цифровых элементов, вызванная дискретизацией по времени.

1.Исследование временных и частотных характеристик нерекурсивного фильтра. Для этого собрать схему рис.3.1 для заданного порядка фильтра. В элементах задержки установить заданный интервал дискретизации.

Для снятия переходной характеристики подать на вход единичный скачок. Зарисовать вид выходного сигнала и определить время переходного процесса.

Для оценки частотных характеристик на вход подается синусоидальный сигнал на частотах ω_пр, ω_0,1 и измеряется амплитуда выходного сигнала. Вычислить коэффициенты преобразования на этих частотах и отметить точки на теоретической АЧХ предварительной подготовки. Измерить коэффициент преобразования на частоте ω_пр+2π/Т. Сделать выводы.

2. Оценка амплитуды выходного сигнала. Включить последовательно схемы рис.3.1 и рис.3.2. Измерить амплитуду выходного сигнала на выходе фильтра по осциллограмме и на выходе вычислителя амплитуды в 5 точках диапазона частот 2π(40÷60) рад./сек. Сделать выводы о точности вычисления амплитуды.

3. Исследование частотных характеристик дискретного фильтра Фурье. Для этого в схеме дискретного фильтра Фурье установить значение основной частоты и заданный интервал дискретизации. Для оценки частотных характеристик подать на вход синусоидальный сигнал в 5 точках диапазона частот 2π(40÷60) рад./сек. Вычислить коэффициенты преобразования на этих частотах и отметить точки на теоретической АЧХ предварительной подготовки и на характеристике п.3.

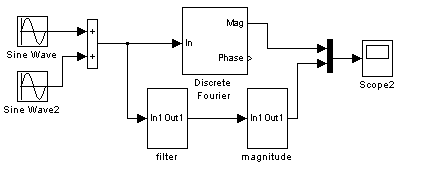
Рис.3.3

4. Собрать схему рис.3.3. На вход подать сумму колебаний u(t)=sin(ω_прt)+sin(ωt), ω=2π(75,100,125,150) рад./сек. Зарисовать осциллограммы вычисления амплитуды. Сделать выводы.