3. Модели технологических процессов на основе законов гидромеханики.

В тех случаях, если в технологических объектах определяющим является процесс переноса массы, то при получении их моделей в основном рассматриваются два механизма – молекулярный и конвективный перенос.

Молекулярный перенос массы происходит вследствие беспорядочного теплового движения микрочастиц. Перенос массы по такому механизму называется диффузией. Экспериментально установлено, что количество переносимого вещества пропорционально градиенту его концентрации. Это положение известно как закон диффузии Фика.

, (3-1)

где, - поток компонента i отнесенный к единице поверхности,

D_i – коэффициент диффузии,

- концентрация компонента i, есть функция пространства и времени,

х – направление переноса.

Знак «-» означает, что поток направлен в сторону уменьшения концентрации.

Коэффициент диффузии является свойством вещества. Его величина определяет скорость переноса частиц компонента i в объеме рассматриваемого вещества. Это свойство вещества называют транспортным. Необходимо учитывать, что коэффициент D меняется с изменением состояния вещества (температуры, давления, состава).

На рис 12 изображен участок трубопровода, где основным механизмом переноса вещества является молекулярный. Выделим элементарный объем и применим к нему законы сохранения массы.

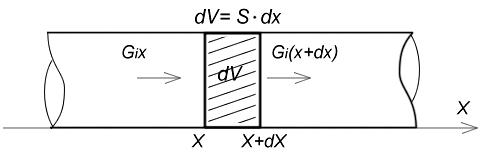
Рис

Рис 12.

- площадь поперечного сечения

Для момента времени t расход вещества i, обусловленный диффузией через поверхность S, находящийся на расстоянии х равен

. (3-2)

На расстоянии dx, концентрация вещества i, вследствие изменения его внутри объема, равна

. (3-3)

Тогда, расход этого вещества через поверхность на расстоянии (x+dx) будет определяться

. (3-4)

Следовательно, за счет изменения концентрации c_i в направлении оси х, в рассматриваемый элементарный объем поступает в единицу времени количество вещества i, равное

, (3-5)

или,

. (3-6)

С другой стороны, изменение количества вещества в выделенном объеме происходит за счет изменения концентрации во времени, т.е.

. (3-7)

Таким образом, на основании закона сохранения массы, с учетом уравнений (3-6) и (3-7), получим

. (3-8)

Тогда, модель процесса в котором основным механизмом является диффузионный перенос, будет иметь следующий вид.

Начальные условия (3-9)

Граничные условия

Это выражение описывает закономерности массопереноса путем молекулярной диффузии и является следствием закона Фика и закона сохранения массы. Уравнение определяет поле концентраций компонента i в рассматриваемой неподвижной среде.

Если рассматриваемая среда представляет собой многокомпонентную смесь, то в общем случае различные ее компоненты перемещаются с различными скоростями. За счет этого состав смеси изменяется в пространстве и времени. Это определяется следующими факторами. Массовым движением, мерой которого является скорость (конвективный перенос) и диффузией, скорость которой зависит от градиента концентрации переносимого компонента и коэффициента диффузии (молекулярный механизм).

Вывод уравнения переноса в движущейся среде аналогичен выводу уравнений, рассмотренных ранее, и сводится к составлению уравнений материально баланса i компонента смеси для элементарного объема

На рис 13 изображен участок трубопровода, в котором перенос вещества осуществляется в результате действия двух механизмов, диффузионного и конвективного переноса с массовой скоростью W(x,t).

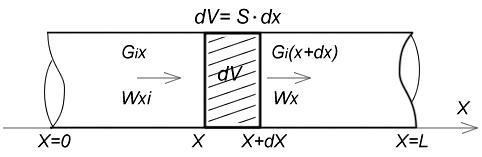
Рис 13.

Тогда количество вещества, поступающего в выделенный элементарный объем будет равно

(3-10 )

Здесь правая часть уравнения характеризует два механизма: - конвективный перенос, и - диффузионный перенос.

А количество вещества, выходящего из выделенного объема, будет определяться следующим выражением

. (3-11)

Изменение количества вещества внутри выделенного объема будет выражаться

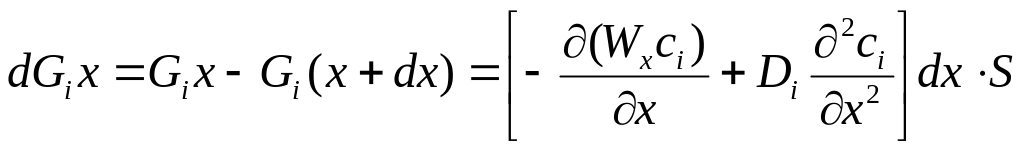. (3-12)

Однако, изменение содержания компонента i в элементарном объеме dV=dxS может происходить не только вследствие диффузионного и конвективного перехода, но и в результате, например, химической реакции притока или оттока вещества из вне. Если скорость образования компонента i в единице объема равна , то за единицу времени в объеме образуется количество этого компонента, равное .

Таким образом, изменение количества компонента i в единице объема с учетом всех механизмов, будет иметь вид

(3-13)

С другой стороны перенос компонента i и его образование вызывает изменение концентрации C_i в рассматриваемом элементарном объеме во времени

(3-14)

На основании закона материального баланса, с учетом уравнений (3-13) и (3-14), получим следующую модель рассматриваемого процесса.

.

(3-15)

Здесь, - начальные условия, определяющие концентрацию вещества i, по координате в начале процесса. Функция - известная.

и - определяют изменение концентрации во времени в начале и конце процесса. и - известные функции.

Это общее выражение, характеризующее перенос массы вещества под действием различных механизмов. В различных частных случаях это уравнение будет иметь соответствующий вид. Эти частные случаи, будут рассмотрены ниже.