1.8. Метод Гаусса. Компьютерная часть

При определении элементов матрицы и операций над ними часто приходится использовать так называемые ранжированные переменные, принимающие значения из заданного промежутка с равными интервалами – шага изменения. Пусть, к примеру, требуется определить ранжированную переменную с начальным значением , конечным значением и с заданным шагом изменения . В этом случае в нужном месте рабочего листа вводится имя переменной , знак присваивания 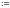и затем через запятую значения и ; после этого клавишей вводится знак и на месте появившейся метки вводится . Если конечное значение при заданном шаге не достигается точно, то последним значением переменной будет наибольшее возможное значение, не превышающее . Выражение можно опускать. В этом случае шаг по умолчанию равен 1 (если больше ) или -1 (если меньше ).

Следует различать знаки равенства и логического равенства, которые на экране почти неразличимы (логический знак равенства отличается только полужирным шрифтом). Знак равенства, вводимый клавишей , используется для получения на экране численного значения выражения, предшествующего этому знаку. Иное – знак логического равенства. Он вводится комбинацией клавиш 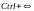и имеет двоякое значение: помимо логических (булевых) выражений, он используется при вводе уравнений, связывая их левые и правые части. Так, щелчок на кнопке подпанели Логические (Boolean) вызывает шаблон для ввода левой и правой частей уравнения.

Для решения систем уравнений в Mathcad используется так называемые блоки решений. Каждому такому блоку должно предшествовать задание начальных (стартовых) значений для искомых переменных. Начинается блок ключевым словом . Затем вводится собственно система уравнений. Завершается блок встроенной функцией 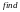, аргументами которой являются переменные системы (допускается векторная форма записи этих переменных). Если система имеет несколько решений, то найденное функцией решение определяется набором начальных значений переменных. Возможно также параметрическое решение системы уравнений с помощью функции относительно параметров , присутствующих в записи этой системы. В этом случае должна быть определена функция решений, зависящая от параметров 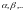. Например, 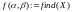. Придавая затем различные значения переменным , получим конкретные решения исходной системы.

1.9. Метод Гаусса. Задачи

1. Доказать утверждения 1 и 2.

2. Пусть система (1.1) имеет решения 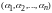и . Найти систему линейных уравнений с теми же коэффициентами при переменных, как и в системе (1.1), имеющую решение

3. Пусть система (1.1) имеет решение . Найти систему линейных уравнений с теми же коэффициентами при переменных, как и в системе (1.1), имеющую решение

4. Решить системы линейных уравнений методом Гаусса:

а) ,

б) ,

в)

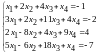
5. Для откорма скота на ферме в ежедневный рацион каждого животного должно включаться 5 видов питательных веществ в количествах 76, 360, 155, 294, 231 единиц соответственно. При этом используется 6 видов кормов, стоимости одной весовой единицы которых равны соответственно 15, 3, 8, 1, 20.5, 13.5 ден. ед. Дана матрица А норм содержания питательных веществ в кормах, в которой на позиции находится число единиц -го вида питательных веществ, содержащихся в единице веса -го вида кормов. Определить состав ежедневного рациона для откорма скота на ферме при дополнительном условии, что общая стоимость всего рациона должна равняться 250 ден. ед.

а) ;

б) .

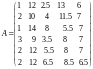6. Для сохранения здоровья человек должен потреблять в сутки определенное количество питательных веществ трех видов, содержащихся в 5 видах пищи. Цена единицы веса пищи каждого вида равна соответственно 10, 5, 6, 8, 10 ден. ед. Суточные нормы питательных веществ равны соответственно 10, 12, 20 единиц. Дана также матрица А норм содержания питательных веществ в единице веса пищи, в которой на позиции находится норма содержания питательного вещества -го вида в единице веса пищи -го вида. Определить количество пищи каждого вида, включаемой в суточную диету при условиях, что вариант диеты должен иметь стоимость в 85 ден. ед., а количество пищи второго типа должно равняться количеству пищи четвертого вида.

а) ;

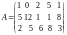б) .

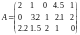7. Предприятие выпускает пять видов продукции, используя при этом сырье трех видов. Дана матрица расхода сырья:

,

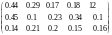в которой на позиции находится величина, равная количеству сырья -го вида, расходуемому на производство единицы продукции -го вида. Запасы сырья по типам составляют 1325, 340, 208 вес. ед. соответственно. Прибыль в ден. ед. за единицу готовой продукции каждого вида равна 16, 10, 14, 12, 12 соответственно. Необходимо спрогнозировать объемы выпуска продукции при следующих условиях: прибыль должна составить 15620 ден. ед., а объемы выпуска продукции второго и первого видов должны быть одинаковы. Определить также зависимость объемов выпускаемой продукции от планируемой величины прибыли, которая должна будет находиться в диапазоне от 15000 до 20000 ден. ед.

8. Доказать следствия 3 и 4.

9. Доказать следствие 1.7.

10. Доказать. теорему 1.13: квадратная матрица А вырождена, если и только если такой является матрица .

11. Доказать теорему 1.14: добавление нового столбца к матрице не нарушает линейную независимость ее строк; аналогично добавление новой строки не нарушает линейную независимость ее столбцов.

12. Доказать теорему 1.15: неоднородная система линейных уравнений с квадратной матрицей А имеет единственное решение, если и только если строки (столбцы) матрицы А линейно независимы.

13. Доказать теорему 1. 16: любую линейно независимую систему векторов, не являющуюся базисом в пространстве , можно дополнить новыми векторами до базиса этого пространства.

14. Доказать следующее утверждение. Теорема 1.17. Пусть дана система из линейно независимых векторов пространства и . Доказать, что если ненулевой вектор ортогонален с каждым вектором из А, то система векторов А, будет также линейно независимой.

15. Доказать, что векторы , , образуют базис в пространстве , а также представить вектор в виде линейной комбинации векторов , , .

а) , , , ;

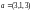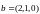б) , , , .

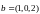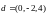16. Дополнить линейно независимую систему векторов до базиса:

а) ;

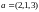б) , ;

в) , ;

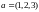г) , ;

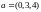д) , ;
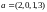