
- •Содержание
- •Глава 1. Общие математические и экономические понятия.
- •1.4. Матрицы. Математическая часть
- •1.5. Матрицы. Компьютерная часть
- •1.6. Матрицы. Задачи
- •1.7. Метод Гаусса. Математическая часть
- •Алгоритм Гаусса
- •1.8. Метод Гаусса. Компьютерная часть
- •1.9. Метод Гаусса. Задачи
- •Ответы, указания, решения.
- •Глава 2. Обратные матрицы и определители
- •2.1. Обратные матрицы. Математическая часть
- •2.2. Обратные матрицы. Задачи
- •2.3. Ответы, указания, решения.
- •2.4. Определители. Математическая часть
- •2.5. Определители. Задачи
- •2.6. Ответы, указания, решения
- •Глава 3. Метод наименьших квадратов
- •3.1. Задачи для самостоятельного решения
- •3.2. Ответы, указания, решения
- •Глава 4. Собственные значения неотрицательных матриц
- •4.1. Задачи для самостоятельного решения
- •4.2. Ответы, указания, решения
- •Глава 5. Балансовые модели многоотраслевой экономики
- •5.1. Компьютерный раздел
- •5.2. Задачи для самостоятельного решения
- •5.3. Ответы, указания, решения Общий алгоритм решения задач 1 а)-в)
- •Глава 6. Модели международной торговли
- •6.1. Задачи для самостоятельного решения
- •6.2. Ответы, указания, решения Общий алгоритм решения задач 1 а)- 1. Е)
- •Литература
4.1. Задачи для самостоятельного решения
1. Доказать следствие 4.1.
2.
Доказать, что если
- собственный вектор некоторой матрицы,
то и вектор
 ,
где
- любое, не равное нулю число, также
является собственным вектором,
соответствующим тому же собственному
значению, что и
-
,
где
- любое, не равное нулю число, также
является собственным вектором,
соответствующим тому же собственному
значению, что и
-
3. Доказать, что система векторов, состоящая из собственных векторов, соответствующих попарно различным собственным значениям некоторой матрицы А, является линейно независимой.
4.
Известно следующее свойство определителя:
для любых двух квадратных матриц С, В
одного порядка
 -Пользуясь этим свойством, доказать,
что собственные значения обратной
матрицы
равны обратным величинам для собственных
значений матрицы А.
-Пользуясь этим свойством, доказать,
что собственные значения обратной
матрицы
равны обратным величинам для собственных
значений матрицы А.
5. Доказать: нуль является собственным значением квадратной матрицы А, если и только если А – вырождена.
6. Пусть А – положительная квадратная матрица. Тогда любой ее неотрицательный собственный вектор является положительным и соответствует максимальному собственному значению матрицы А.
7.
Пусть А – положительная квадратная
матрица. Тогда любые два ее положительных
собственных вектора
и
линейно зависимы, т.е.
 для некоторого положительного числа
.
для некоторого положительного числа
.
8. Для данной матрицы А найти все ее собственные значения и собственные векторы, им соответствующие.
а)
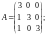 б)
б)
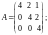 в)
в)
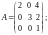 г)
г)
 ;
д)
;
д)
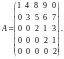
4.2. Ответы, указания, решения
Указание. Утверждение непосредственно проверяется по определению.
Доказательство. Докажем индукцией относительно числа векторов в системе. Для одного вектора утверждение следует из задачи 8 п.1.3. Предположим, что утверждение верно для систем с векторами. Пусть
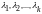 -
попарно различные собственные значения
матрицы А,
-
попарно различные собственные значения
матрицы А,
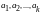 -
собственные векторы, им соответствующие.
Если система векторов
-
линейно зависима, то нулевой вектор
представим в виде ненулевой комбинации
этих векторов:
-
собственные векторы, им соответствующие.
Если система векторов
-
линейно зависима, то нулевой вектор
представим в виде ненулевой комбинации
этих векторов:
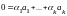 -
Умножим обе части этого равенства слева
на матрицу
-
Умножим обе части этого равенства слева
на матрицу
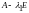 :
:

или

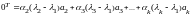 .
.
Так
как по индуктивному предположению
система векторов
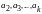 линейно независима, то из последнего
равенства следует, что все коэффициенты
линейно независима, то из последнего
равенства следует, что все коэффициенты
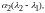
 … ,
… ,
 равны нулю. Но тогда
равны нулю. Но тогда
 ,
ибо все числа
,
ибо все числа
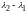 ,
,
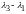 ,…,
,…,
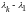 отличны от нуля. Следовательно,
отличны от нуля. Следовательно,
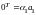 ,
т.е.
,
т.е.
 .
Получено противоречие, поскольку
рассмотренная комбинация векторов
ненулевая.
.
Получено противоречие, поскольку
рассмотренная комбинация векторов
ненулевая.
Доказательство. Поскольку предполагается, что обратная матрица существует, то матрица А не имеет нулевого собственного значения (см. задачу 5 и следствие 2.2). Предположим, что
 -
собственное значение матрицы А. Это
равносильно равенству
-
собственное значение матрицы А. Это
равносильно равенству
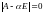 (теорема
4.1). Разделив каждую строку матрицы
на
,
получим равенство
(теорема
4.1). Разделив каждую строку матрицы
на
,
получим равенство
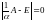 .
Теперь умножим обе части этого равенства
на
.
Теперь умножим обе части этого равенства
на
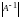 :
:
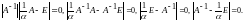
И,
опять таки, по теореме 4.1 последнее
равенство равносильно тому, что
 - собственное значение матрицы
.
Утверждение доказано.
- собственное значение матрицы
.
Утверждение доказано.
Указание: воспользоваться следствием 1.3.
Доказательство. Согласно теореме 4.2 и следствию 4.1, существует положительный вектор , такой, что . Пусть теперь - произвольный неотрицательный собственный вектор матрицы А, т.е.
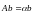 для некоторого собственного значения
.
Если
-я
координата в
равна нулю, то произведение
-й
строки
для некоторого собственного значения
.
Если
-я
координата в
равна нулю, то произведение
-й
строки
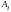 матрицы А на
было бы равно нулю, что невозможно ввиду
матрицы А на
было бы равно нулю, что невозможно ввиду
 ,
, и
и
 .
Поэтому
-
положительный собственный вектор.
Применяя теоремы 1.1 и 1.14, с одной стороны,
имеем:
.
Поэтому
-
положительный собственный вектор.
Применяя теоремы 1.1 и 1.14, с одной стороны,
имеем:
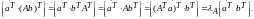
С другой стороны,
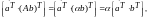
Откуда
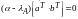 .
.
Но
 ввиду того, что
ввиду того, что
 .
Поэтому
.
Поэтому
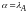 ,
что и требовалось доказать.
,
что и требовалось доказать.
Доказательство. Векторы и соответствуют максимальному собственному значению матрицы А (см. задачу 6), т.е. ,
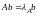 .
Обозначим через
положительное
число, равное наименьшему из чисел
.
Обозначим через
положительное
число, равное наименьшему из чисел
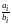 ,
где
,
где
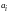 ,
,
 -
-е
координаты векторов
и
соответственно. Тогда
-
-е
координаты векторов
и
соответственно. Тогда
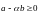 ,
причем хотя бы одна координата вектора
,
причем хотя бы одна координата вектора
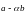 равна нулю (согласно выбору
).
Но
равна нулю (согласно выбору
).
Но
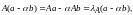
что
означает, что
- собственный, не являющийся положительным,
неотрицательный вектор матрицы А, что
\будет противоречить утверждению задачи
6, если только
- ненулевой. Поэтому
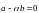 ,
что и требовалось доказать.
,
что и требовалось доказать.
8.
Решение.
Для
определения собственных значений
матрицы А составим характеристическое
уравнение
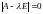 :
:
 .
.
Так
как определитель треугольной матрицы
равен произведению элементов на главной
диагонали, то данное уравнение равносильно
уравнению
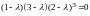 ,
откуда получаем три собственных значения
,
откуда получаем три собственных значения
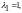
 ,
,
 .
Для определения собственных векторов,
им соответствующих, необходимо решить
три однородные системы линейных уравнений
.
Для определения собственных векторов,
им соответствующих, необходимо решить
три однородные системы линейных уравнений
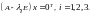 Применим
алгоритм метода Гаусса для решения
первой из них:
Применим
алгоритм метода Гаусса для решения
первой из них:
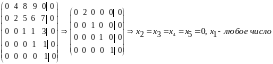 .
.
Итак,
все собственные векторы, соответствующие
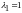 имеют вид
имеют вид
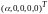 ,
где
-
любое число. Аналогично устанавливается,
что все собственные векторы, соответствующие
,
имеют вид
,
где
-
любое число. Аналогично устанавливается,
что все собственные векторы, соответствующие
,
имеют вид
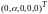 ,
где
- любое число. Решим последнюю систему:
,
где
- любое число. Решим последнюю систему:
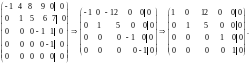
Итак,
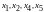 - базисные переменные,
- свободная переменная:
- базисные переменные,
- свободная переменная:
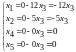 .
.
Поэтому
собственные векторы, соответствующие
,
имеют следующий вид:
 ,
-
любое число.
,
-
любое число.
