Пример 2

Условия задачи: Определить напряжения от собственного веса грунта и построить эпюры их распределения для двух расчетных схем:

1) при отсутствии грунтовых вод;

2) при наличии грунтовых вод на глубине 2 м от поверхности.

Характеристики слоев грунта приведены в таблице 2.1.

Таблица 2.1

№ грунта	Тип грунта	Толщина слоя h, м	Глубина уровня грунтовых вод WL, м	Удельный вес грунта γ, кН/м3	Удельный вес частиц грунта γs, кН/м3	Коэффициент пористости е	Показатель текучести IL
1	Песок мелкий	5	2	18,6	26,7	0,72	-
2	Глина	3	-	19,1	27	0,74	– 0,1

Решение

1) Схема 1 (грунтовые воды отсутствуют).

Точка 0 (на поверхности земли): z₀ = 0; σ_zg,0 = 0.

Точка 1 (на границе песка и глины): z₁ = 5 м; σ_zg,1 = γ₁ ·h₁ = = 18,6 ·5 = 93 кПа (по формуле (2.1).

Точка 2 (на подошве глины): z₂ = 8 м; σ_zg,2 = ∑γ_i · h_i = σ_zg,1 +

+ γ₂ · h₂ = 93 + 19,1· 3 = 150,3 кПа (по формуле (2.3).

2) Схема 2. В песке на глубине 2 м имеются грунтовые воды, значит, удельный вес этого грунта ниже WL принимается с учетом взвешивающего действия воды по формуле 2.4:

= (26,7 – 10)/(1 + 0,72) = 9,71 кН/м³.

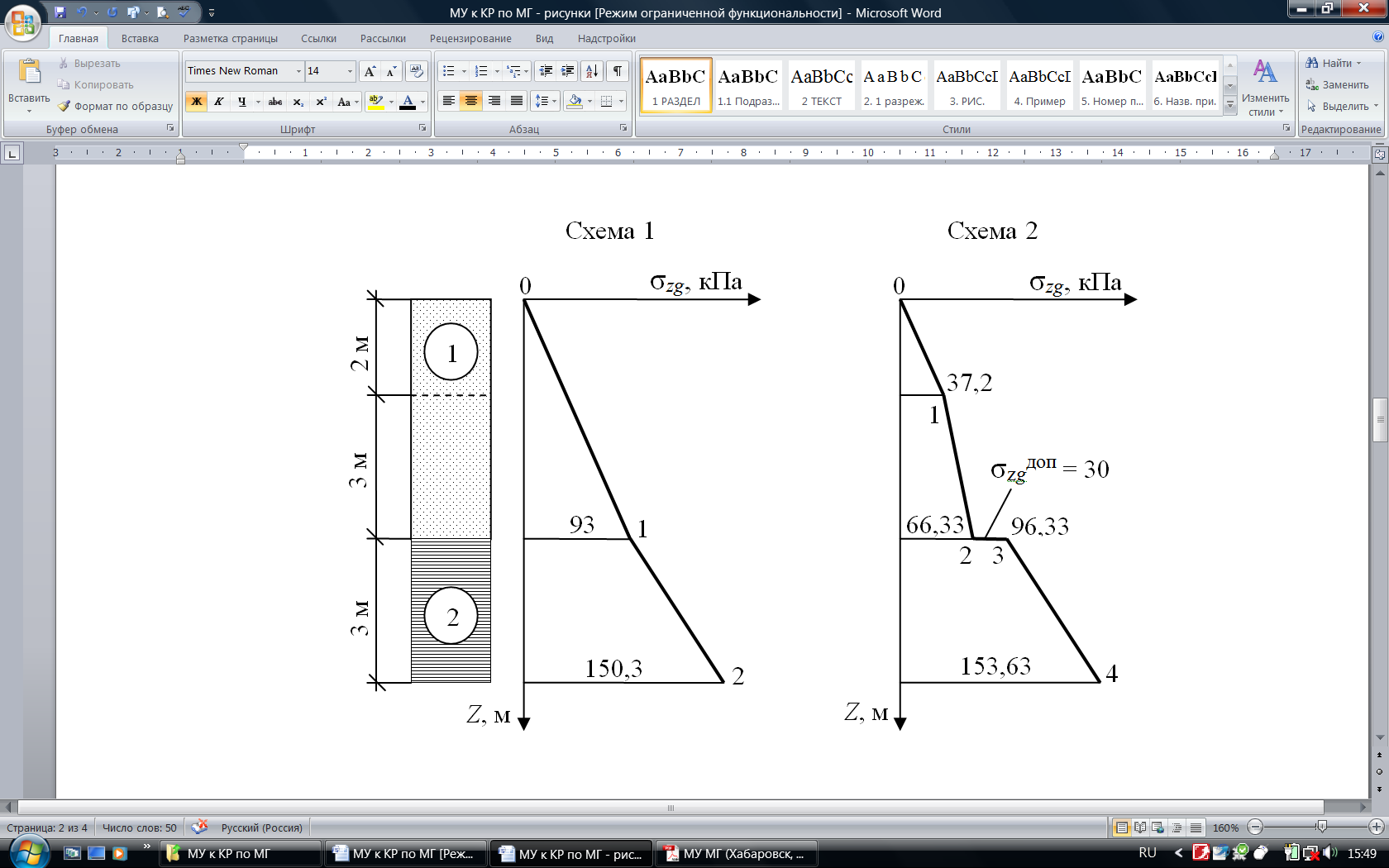
Рисунок 2.2 – Эпюры распределения напряжений

от собственного веса грунта

Глина имеет показатель текучести I_L = – 0,1 < 0,25, значит, ее удельный вес принимается без учета взвешивающего действия воды, а для определения σ_zg в этом слое и ниже его следует учитывать давление столба воды, расположенного выше этого слоя по формуле 2.5:

σ_zg^доп = g_W · a_W = 10 · 3 = 30 кПа.

Точка 0 (на поверхности земли): z₀ = 0; σ_zg,0 = 0.

Точка 1 (на кровле WL): z₁ = 2 м; σ_zg,1 = γ₁ · h₁ = 18,6 · 2 = = 37,2 кПа (по формуле 2.1).

Точка 2 (на кровле глины): z₂ = 5 м; σ_zg,2 = ∑γ_i · h_i = σ_zg,1 + γ₂ · h₂ = = 37,2 + 9,71 · 3 = 66,33 кПа (по формуле 2.3).

Точка 3 (на кровле глины с учетом σ_zg^доп): z₃ = 5 м; σ_zg,3 = σ_zg,2 + + σ_zg^доп = 66,33 + 30 = 96,33 кПа.

Точка 4 (на подошве глины): z₄ = 8 м; σ_zg,4 = ∑γ_i · h_i = σ_zg,3 + + γ₂ · h₂ = 96,33 +  19,1 · 3 = 153,63 кПа (по формуле 2.3).

Задача 3

определение напряжений в массиве грунта от действия сосредоточенной силы

Определение напряжений в грунтовой толще от действия внешних нагрузок необходимо для установления условий прочности и устойчивости грунтов, расчета деформаций оснований.

В большинстве практических случаев при решении вопроса о распределении напряжений в грунтах в механике грунтов применяют теорию линейно деформируемых тел. Для определения напряжений по этой теории будут полностью справедливы уравнения теории упругости, также базирующиеся на линейной зависимости между напряжениями и деформациями (закон Гука).

В соответствии с решениями теории упругости от действия силы Р в любой точке полупространства М на глубине z и на расстоянии r от точки приложения нагрузки возникает сложное напряженное состояние, характеризуемое в декартовой (прямоугольной) системе координат шестью составляющими напряжений (тремя нормальными – σ_x, σ_y, σ_z, и тремя касательными – τ_xy, τ_yz, τ_zx).

Для практических расчетов наибольшее значение имеют вертикальные сжимающие напряжения σ_z (рисунок 3.1), вычисляемые по формуле

, (3.1)

где .

Табулированные значения коэффициента К, зависящие от отношения r/z приведены в таблице 3.1.

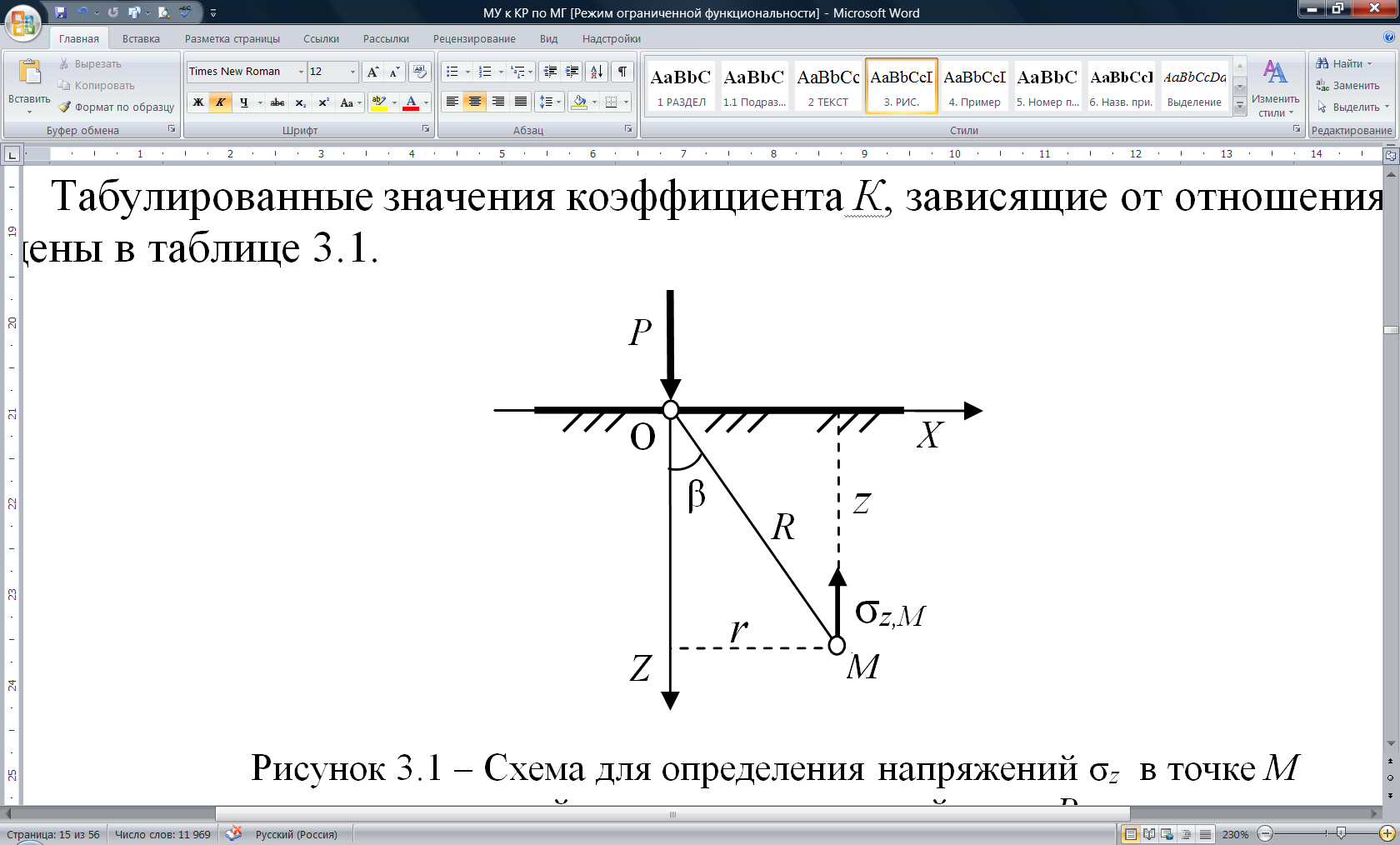
Рисунок 3.1 – Схема для определения напряжений σ_z

в точке М от действия сосредоточенной силы Р

Таблица 3.1 – Значения коэффициента К для определения σ_z при различных отношениях r/z

r/z	К	r/z	К	r/z	К	r/z	К
0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45	0,4775 0,4745 0,4657 0,4516 0,4329 0,4103 0,3849 0,3577 0,3294 0,3011	0,50 0,55 0,60 0.65 0,70 0,75 0,80 0,85 0,90 0,95	0,2733 0,2466 0,2214 0,1978 0,1762 0,1565 0,1386 0,1226 0,1083 0,0956	1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 1,45	0,0844 0,0744 0,0658 0,0581 0,0513 0,0454 0,0402 0,0357 0,0317 0,0282	1,50 1,60 1,70 1,80 1,90 2,00 2,50 3,00 4,00 5,00	0,0251 0,2000 0,0160 0,0129 0,0105 0,0085 0,0034 0,0015 0,0004 0,0001

Для выполнения задачи № 3 необходимо выбрать исходные данные из таблицы А.3 приложения А. Выбор варианта задания производится по сумме последних трех цифр зачетки.