- •Электротехника с основами электроники Общие методические указания
- •Литература
- •Раздел 1.Общая электротехника
- •Раздел 2. Основы электроники
- •Задача №1
- •Задача №2
- •Задача №3
- •Задача №4
- •Задача №5 Варианты 1-10
- •Задача №6 Варианты 1-10
- •Задача №7
- •Варианты 5-8
- •Технические данные полупроводниковых приборов
- •Методические указания по выполнению контрольной работы Указания к решению задачи №1
- •Указания к решению задач 2, 3 и 4.
- •Решение.
- •Указания к решению задачи №5
- •Указания к решению задачи№6
- •Указания к решению задачи№7
Технические данные полупроводниковых приборов
Тип диода Iдоп, А Uобр, В Тип диода Iдоп, А Uобр, В
Д7Г 0,3 200 Д217 0,1 800
Д205 0,4 400 Д218 0,1 1000
Д207 0,1 200 Д221 0,4 400
Д209 0,1 400 Д222 0,4 600
Д210 0,1 500 Д224 5 50
Д211 0,1 600 Д224А 10 50
Д214 5 100 Д224Б 2 50
Д214А 10 100 Д226 0,3 400
Д214Б 2 100 Д226А 0,3 300
Д215 5 200 Д231 10 300
Д215А 10 200 Д231Б 5 300
Д215Б 2 200 Д232 10 400
Д233 10 500 Д232Б 5 400
Д233Б 5 500 Д244 5 50
Д234Б 5 600 Д214А 10 50
Д242 5 100 Д244Б 2 50
Д242А 10 100 Д302 1 200
Д242Б 2 100 Д303 3 150
Д243 5 200 Д304 3 100
Д243А 10 200 Д305 6 50
Д243Б 2 200 КД202А 3 50
КД202Н 1 500
Методические указания по выполнению контрольной работы Указания к решению задачи №1
Перед выполнением контрольной работы ознакомьтесь с общими методическими указаниями. Решение задач сопровождайте краткими пояснениями.
Решение задач этой группы требует знания законов Ома, для всей цепи и её участков, первого и второго законов Кирхгофа, методики определения эквивалентного сопротивления цепи смешанном соединении резисторов, а также умения вычислять мощность и работу электрического тока.
Пример 1.
Для схемы, приведённой на рис. 41 а, определить эквивалентного сопротивления цепи RAB и токи в каждом резисторе, а также расход электрической энергии цепью за 8ч работы.
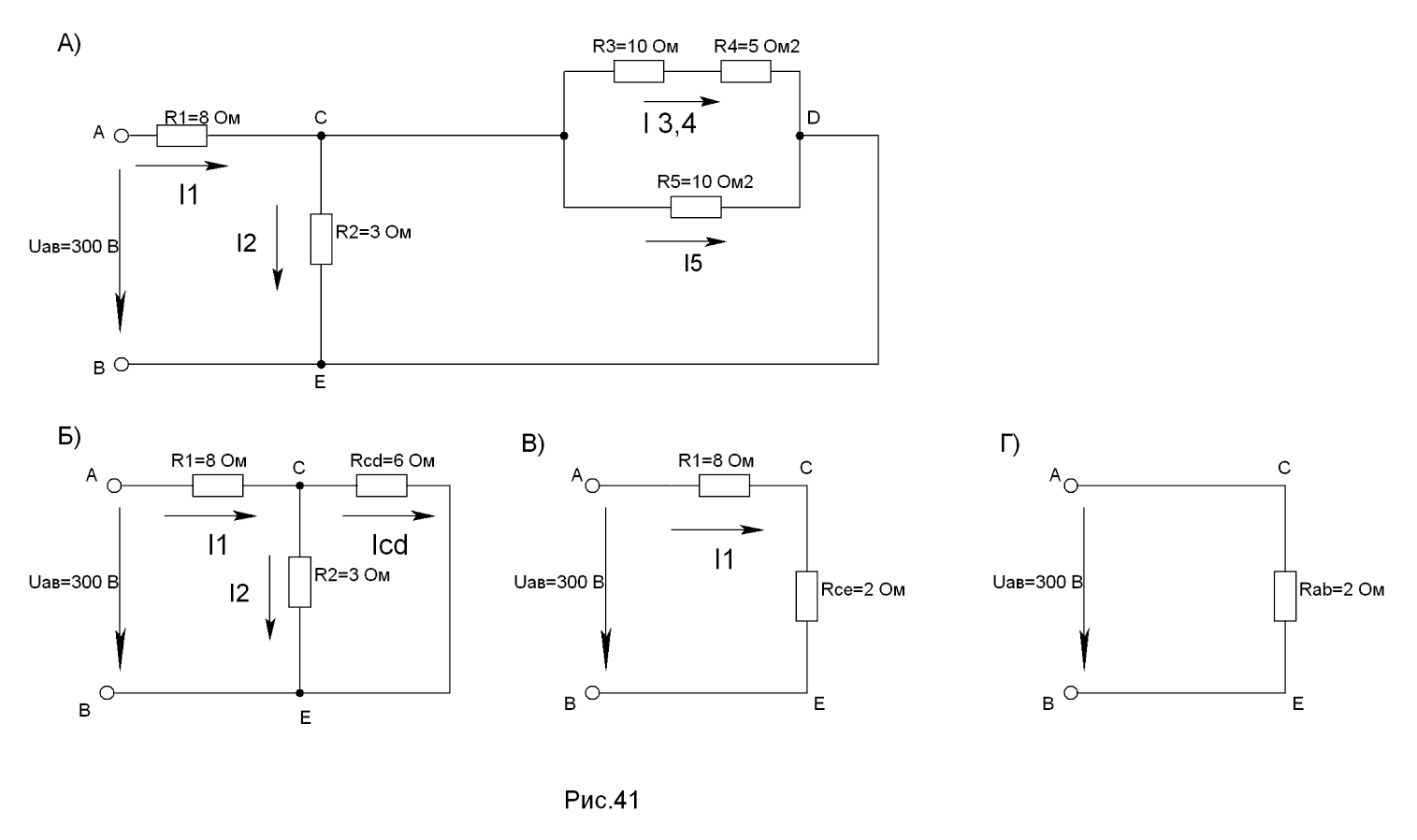
Решение. Задача относится к теме “Электрические цепи постоянного тока”. Проводим поэтапное решение, предварительно обозначив стрелкой, ток в каждом резисторе, индекс тока должен соответствовать номеру резистора, по которому он проходит.
1.Определяем общее сопротивление разветвления CD, учитывая, что резисторы R3 и R4 соединены между собой последовательно, а с резистором R5- параллельно:
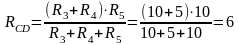 Ом
Ом
2. Определяем общее сопротивления цепи относительно зажимов СЕ.
Так как резистор RCD и R2 включены параллельно, то:
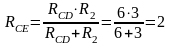 Ом
(рис.41, в).
Ом
(рис.41, в).
3. Находим эквивалентное сопротивление всей цепи:
 Ом
(рис.41, г).
Ом
(рис.41, г).
4. Определяем ток в сопротивлениях цепи. Так как напряжение UАВ приложено ко всей цепи, а RАВ=10 Ом, то, согласно закону Ома:
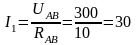 А.
А.
Внимание! Нельзя последнюю формулу писать в виде:

так как UАВ приложено ко всей цепи, а не к участку R1
Для определения тока I2 нужно найти напряжение на резисторе R2, т.е. UСЕ. Очевидно , UCE меньше UAB на величину потери напряжения в резисторе R1, т.е. UCE=UAB-I1R1=300-30*8=60 В. Тогда
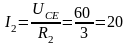 А.
А.
Так как UCE=UCD, то можно определить токи I3,4 и I5:
 А;
А;
 А
А
С помощью Кирхгофа, записанного для узла С, проверим правильность определения токов:
 ,
30=20+4+6.
,
30=20+4+6.
5. Расход энергии цепью за 8 ч работы:
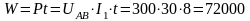 Вт*ч=72
кВт*ч
Вт*ч=72
кВт*ч
Указания к решению задач 2, 3 и 4.
Эти задачи относятся к неразветвлённым и разветвленным цепям и перемоткам, трёхфазным цепям переменного тока. Перед их решениям изучить соответствующие разделы. Ознакомитесь с методикой построения векторных диаграмм.
Пример 1.
В неразветвлённой цепи переменного тока R1=20 Ом, R2=4 Ом, XL1=4 Ом, XL2=6 Ом, XC1=2 Ом.
Подведённое напряжение U =40 В.
Определить: полное сопротивление Z, ток I, коэффициент мощности cosφ, полную мощность S, активную мощность P, реактивную мощность G.
Построить в масштабе векторную диаграмму.
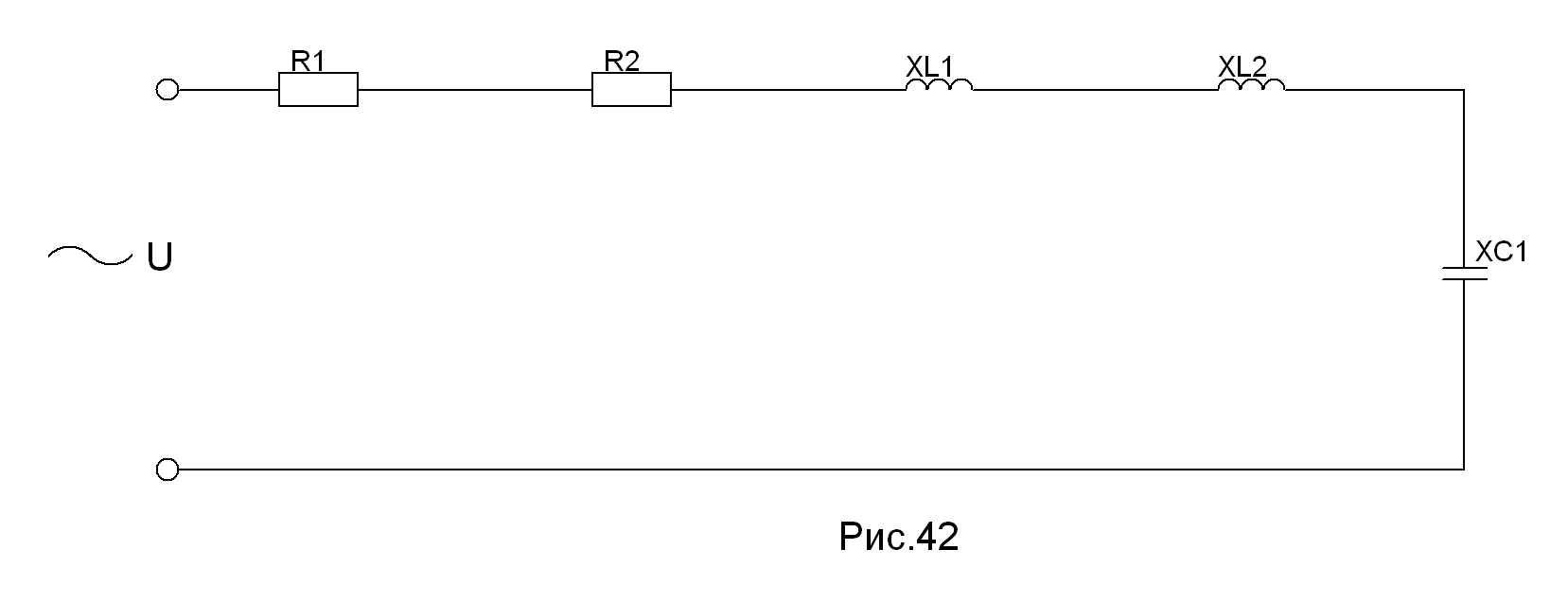
Решение
Полное сопротивление цепи определяется по формуле:

где
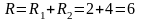 Ом -
активное суммарное сопротивление цепи.
Ом -
активное суммарное сопротивление цепи.
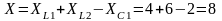 Ом
Ом
-сумма индуктивных и емкостных сопротивлений. Тогда:
 Ом
Ом
По закону Ома для цепи переменного тока находим ток в цепи:
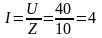 А
А
Коэффициент мощности cosφ:

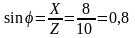
Определяем полную мощность:


Активная мощность:
P = U·I ·cos j=40·4·0,6 = 96Вт
Реактивная мощность:
Q= U·I ·sin j=40·4·0,8 = 128 вар
Для построения векторной диаграммы определим падение напряжение на сопротивлениях:
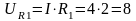 В
В
 В
В
 В
В
 В
В
Для рассматриваемого примера задаёмся масштабом:
по току:
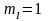
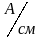
по напряжению:
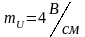
Длина векторов напряжений:
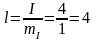 см
см
Длина векторов напряжений:
 см
см
 см
см
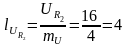 см
см
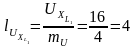 см
см
 см
см
Поскольку ток является одинаковой величиной для всех сопротивлений, диаграмму строим относительно вектора тока.
1. Горизонтально в масштабе откладываем вектор тока.
2. Вдоль вектора тока откладываем векторы UR1 и UR2
3.
Под углом 90˚ откладываем векторы
напряжения
 и
и
 в
сторону опережения вектора тока (вверх),
т.к. положительное вращение векторов
принято против часовой стрелки.
в
сторону опережения вектора тока (вверх),
т.к. положительное вращение векторов
принято против часовой стрелки.
4. Под углом 90˚ к вектору тока откладываем вниз вектор напряжения на ёмкостном сопротивлении.
5.
Векторы
 ,
,
 ,
,
,
,
,
,
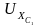 ,
откладываем по правилу сложения векторов,
в результате чего получаем вектор
приложенного напряжения:
,
откладываем по правилу сложения векторов,
в результате чего получаем вектор
приложенного напряжения:
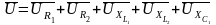
Угол
φ между векторами общего напряжения
 и тока I
называется углом сдвига фаз между током
и напряжением.
и тока I
называется углом сдвига фаз между током
и напряжением.
По виду векторной диаграммы необходимо научится определять характер нагрузки.
В нашем случае напряжение опережает ток: нагрузка имеет активно –индуктивный характер
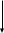

UL2
UC1

U
UL1
φ




UR1 I UR2
Рис.43
Пример 2.
Катушка
с активным сопротивлением R1
= 4 Ом и
индуктивным
 Ом соединена параллельно с конденсатором,
ёмкостное сопротивление которого
Ом соединена параллельно с конденсатором,
ёмкостное сопротивление которого
 Ом и активным
сопротивлением R2
=6 Ом. К цепи приложено напряжение U=60
В. Определить: 1.Токи в ветвях и в
неразветвленной части цепи; 2. Активные
и реактивные мощности каждой ветви и
всей цепи. 3.Полную мощность цепи; 4. Углы
сдвига фаз между током и напряжением в
каждой ветви и во всей цепи. Начертить
в масштабе векторную диаграмму.
Ом и активным
сопротивлением R2
=6 Ом. К цепи приложено напряжение U=60
В. Определить: 1.Токи в ветвях и в
неразветвленной части цепи; 2. Активные
и реактивные мощности каждой ветви и
всей цепи. 3.Полную мощность цепи; 4. Углы
сдвига фаз между током и напряжением в
каждой ветви и во всей цепи. Начертить
в масштабе векторную диаграмму.
Решение.
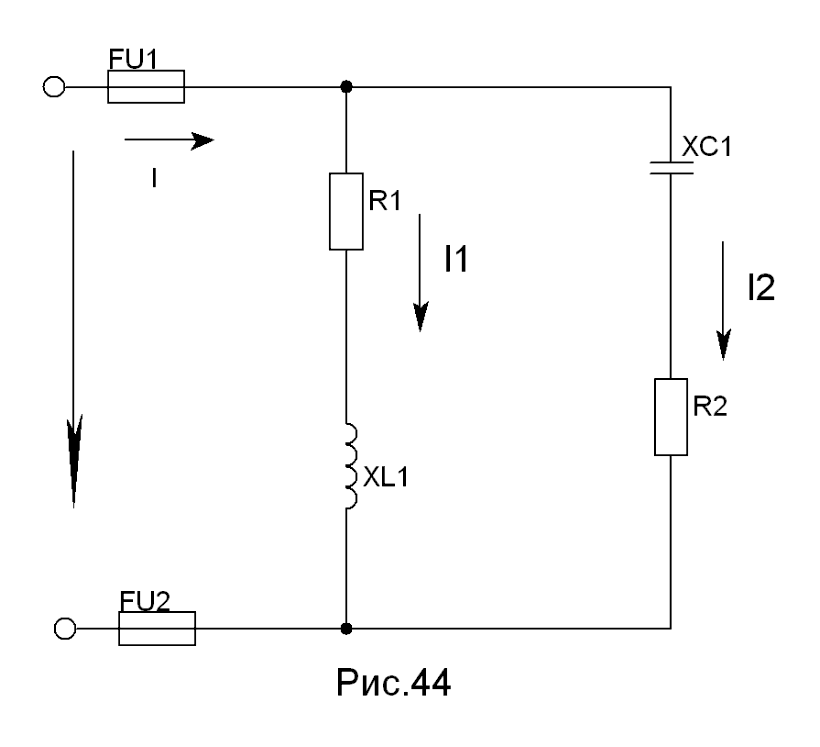
Определить токи в ветвях:
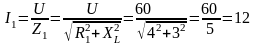 А
А
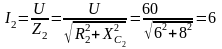 А
А
Углы сдвига фаз в ветвях:
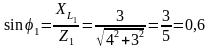
по таблицам Брадиса находим φ1=36˚50΄, т.к. φ1>0, то напряжение опережает ток:
 ;
φ2=-53˚10΄,
;
φ2=-53˚10΄,
т.е. напряжение отстаёт от тока, так как φ2<0.
По таблицам Брадиса находим:

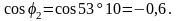
3. Определяем активные и реактивные составляющие токов в ветвях:
 А
А
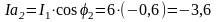 А
А
 А
А
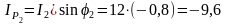 А
А
4. Определяем ток в неразветвленной части цепи:
 А
А
5. Определить коэффициент мощности всей цепи:

Определяем активные и реактивные мощности ветвей и всей цепи:
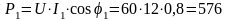 Вт
Вт
 Вт
Вт
 Вт
Вт
 вар
вар
 вар
вар
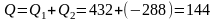 вар
вар
Определяем полную мощность всей цепи:
 ВА
ВА
Ток в неразветвленной части цепи можно определить и таким образом:
 А
А
Для построения векторной диаграммы задаёмся масштабом по току и напряжению:
I см - 2 А
I см - 5 В
Построение начинаем с вектора напряжения U.
Под углом φ1, к нему (в сторону отставания) откладываем в масштабе вектор тока I1, под углом φ2 (в сторону отставания) - вектор тока - I2. Геометрическая сумма этих токов ровна току в неразветвленной части цепи.
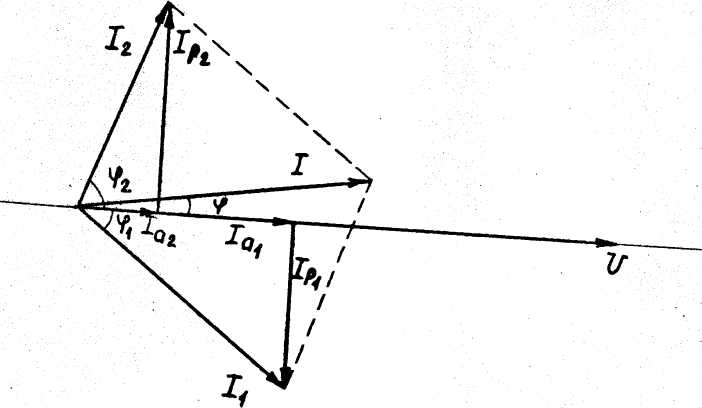
Рис.45
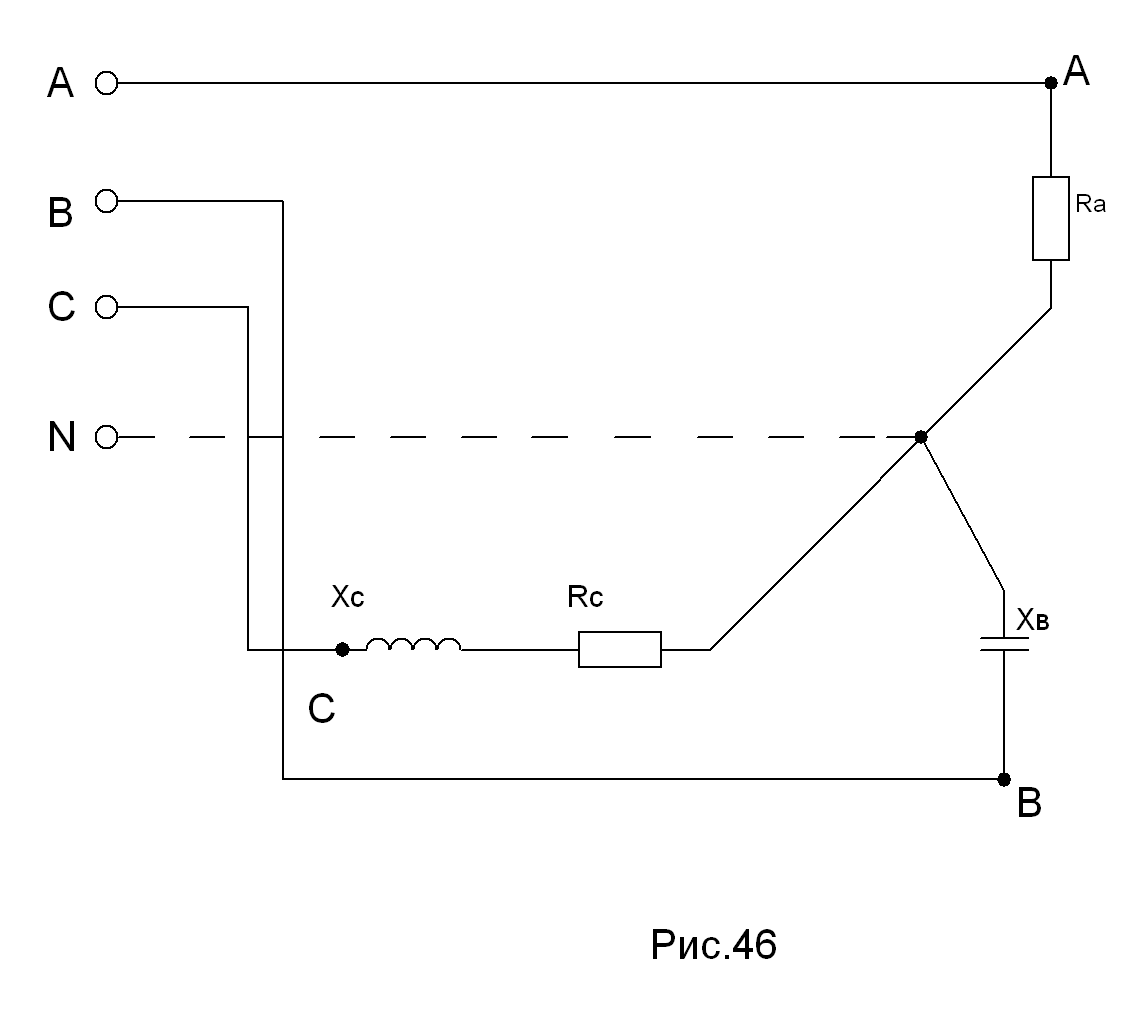
Пример 3.
В трёхфазную четырехпроводную сеть включили звездой несимметричную нагрузку: в фазу А - активное сопротивление RA =11 Ом, в фазу В - емкостное сопротивление XB=10 Ом, в фазу С - активное сопротивление RС=8 Ом и индуктивное XС=6 Ом. Линейное напряжение сети UН=380 В.
Определить фазные токи, активную и полную мощности, потребляемые цепью, значение фазных углов, начертить в масштабе векторную диаграмму цепи и найти графически ток в нулевом проводе.