5. Сравнительный анализ сортировок
Мы получили следующие алгоритмы:
I. Сортировки обменом:
Сортировка простым обменом (метод пузырька)
Сортировка простым обменом с флагом
Сортировка простым обменом с границей
Шейкер-сортировка
Быстрая сортировка
II. Сортировки включениями
Сортировка простым включением
Сортировка бинарными вставками
Сортировка Шелла
III. Сортировки выбором
Сортировка простым выбором
Пирамидальная сортировка
Попробуем провести сравнительный анализ их эффективности.
Пусть n – по прежнему обозначает число сортируемых элементов, а С и М – соответственно количество необходимых сравнений ключей и пересылок элементов. Для всех трех простых методов сортировки можно дать замкнутые аналитические формулы. Они приведены в следующей таблице (заголовки столбцов Min, Max, Средн. определяют максимумы, минимумы и ожидаемые средние значения для всех n! перестановок n элементов):
Таблица: Сравнение простых методов сортировки
|
Min |
Средн |
Max |
Простые включения |
C=n-1 M=2(n-1) |
(n2+n-2)/4 (n2-9n-10)/4 |
(n2-n)/2-1 (n2+3n-4)/2 |
Простой выбор |
C=(n2-n)/2 M=3(n-1) |
(n2-n)/2 n(lnn+0,57) |
(n2-n)/2 n2/4+3(n-1) |
Простой обмен (метод пузырька) |
C=(n2-n)/2 M=0 |
(n2-n)/2 (n2-n)*0,75 |
(n2 -n)/2 (n2-n)*1,5 |
Для усовершенствованных
методов нет достаточно простых и точных
формул (некоторые приблизительные
оценки см. в приложении, таблица 4). Все,
что можно сказать, это то, что стоимость
вычислений равна
в случае сортировки Шелла и
в случаях пирамидальной и быстрой
сортировок.
Эти формулы дают
лишь приблизительную оценку эффективности
как функции от n; они
допускают классификацию алгоритмов
сортировки на простые (n2)
и усовершенствованные, или «логарифмические»
(n∙logn).
Однако для практических целей полезно
иметь некоторые экспериментальные
данные, которые могут пролить свет на
коэффициенты
,
позволяющие проводить дальнейшую оценку
различных методов.
Рассмотрим экспериментально полученные данные на примере массивов из 160, 2560 и 10240 элементов (см. приложение, таблицы 1-3). Массивы различной длины и различной начальной упорядоченности (по возрастанию, по убыванию, не упорядоченные) были отсортированы в порядке возрастания и убывания.
Анализируя полученные данные, нетрудно заметить, что сортировка методом пузырька (с улучшениями) определенно является наихудшей среди всех сравниваемых методов, и даже ее улучшенная версия – шейкер-сортировка – все-таки хуже, чем сортировка простыми включениями и простым выбором (кроме патологического случая сортировки уже рассортированного массива).
Очевидно также, что преимущество сортировки бинарными включениями по сравнению с сортировкой простыми включениями ничтожно, хотя оба этих метода заметно превосходят алгоритмы сортировки обменом.
Наиболее выгодными алгоритмами являются быстрая и пирамидальная сортировки, причем быстрая сортировка превосходит пирамидальную в отношении 2 к 3. Она сортирует массив с элементами, расположенными в обратном порядке практически так же, как уже рассортированный массив.
Результаты практически того же порядка показывает сортировка Шелла, особенно в случае уже рассортированного массива. Однако в случае неупорядоченного массива ее эффективность заметно снижается при увеличении количества элементов массива.
С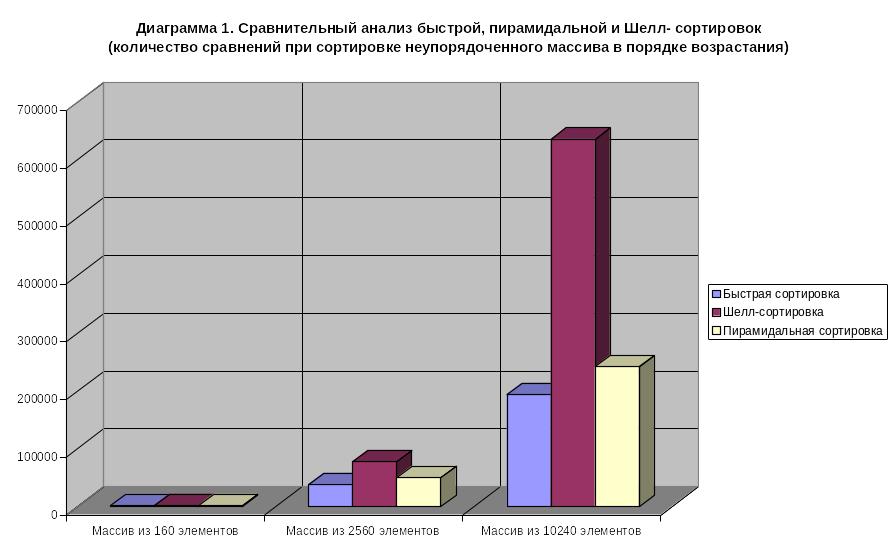
ледующие
диаграммы иллюстрируют сравнительный
анализ трех наиболее выгодных сортировок
(быстрой, пирамидальной и Шелл- сортировок)
применительно к неупорядоченным массивам
различной длины при их сортировке в
порядке увеличения ключей.
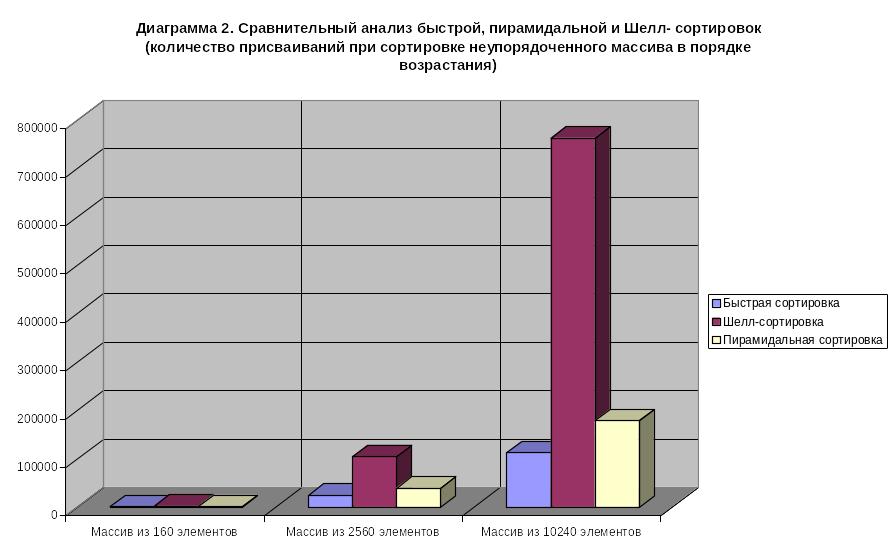
Таким образом, самым быстрым методом и действительно лучшим алгоритмом сортировки оказалась быстрая сортировка, а наихудшим – сортировка методом пузырька.