2.4. Принцип неопределенности Гейзенберга

В 1927 г. В. Гейзенберг (Германия) постулировал принцип неопределенности, согласно которому положение и импульс микрочастицы принципиально невозможно определить в любой момент времени с абсолютной точностью. В каждый момент времени можно определить только лишь одно из этих свойств.

Принцип неопределенности Гейзенберга

Положение и скорость электронов не поддаются одновременному определению с абсолютной точностью:

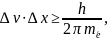
где 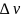– ошибка в определении скорости, 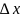– ошибка в определении координаты электрона с массой .

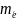Если бы удалось измерить координату частицы так точно, что то ошибка в измерении импульса стала бы бесконечно большой (и наоборот).

Чем точнее определены координаты микрочастицы, тем больше неопределенности в определении скорости и наоборот.

3. Вероятность нахождения электрона в пространстве. Квантовые числа

Таким образом, можно говорить только о вероятности нахождения электрона в данной части пространства. В связи с этим в квантовой механике состояние микрочастицы полностью описывается не ее координатой и скоростью, а некоторой функцией. Эта математическая величина называется волновой функцией или орбиталью и обозначается греческой буквой «пси» ψ.

Физический смысл имеет не сама волновая функция, а только произведение квадрата ее модуля на элементарный объем 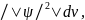равное вероятности нахождения электрона в элементарном объеме

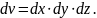
Часть пространства, где наиболее вероятно нахождение электрона, называется электронным облаком.

В 1927 г. австрийский физик Шрёдингер выводит уравнение, связывающее волновую функцию с потенциальной и полной энергией электрона. Не вдаваясь в анализ уравнения Шрёдингера, укажем, лишь, что решить его – значит найти удовлетворяющую ему волновую функцию ψ.

С точки зрения квантово-механической модели атома главное квантовое число можно определить следующим образом.

3.1. Главное квантовое число n характеризует размеры электронного облака и общий уровень энергии электрона в атоме.

n = 1, 2, 3, 4, 5, 6, 7

K, L, N, O, P, Q.

Состояние электрона в атоме, которое характеризуется определенным значением главного квантового числа n, называется энергетическим уровнем.

3.2. Орбитальное квантовое число l характеризует форму электронного облака.

s – облако p – облако d –облако f – облако

имеет более

сложную

форму

l = 0 l = 1 l = 2 l = 3

На первом энергетическом уровне могут находиться только s – облака. Иными словами,

если n = 1, l = 0;

если n = 2, l = 0, 1;

если n = 3, l = 0, 1, 2;

если n = 4, l = 0, 1, 2, 3, ⇒ .

Состояние электрона, которое характеризуется определенным значением l, называется энергетическим подуровнем.

3.3. Магнитное квантовое число характеризует ориентацию электронного облака в пространстве.

Любые возможные расположения s – облака в пространстве идентичны, поэтому s – состоянию соответствует единственное значение магнитного квантового числа

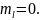
p- облака могут располагаться в пространстве тремя различными способами, поэтому для p - состояния возможны три различных значения:

Для d – состояния возможны пять значений магнитного квантового числа, для f – состояния – семь значений (см. табл.3).

Таблица 3

Электронный подуровень	Возможные значения	Количество орбиталей	Условное изображение
1s	0	1
2p	-1, 0, +1	3
3d	-2, -1, 0, +1, +2	5
4f	-3, -2, -1, 0, +1,+2, +3	7

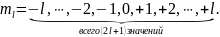
Энергии электронных облаков одного и того же размера и формы, но различным образом ориентированных в пространстве, начинают различаться только при наложении магнитного поля, отсюда и произошло название магнитного квантового числа.

Состояние электрона в атоме, характеризующееся определенными значениями s, l и , называется атомной электронной орбиталью или квантовой ячейкой.

Графически орбиталь обозначается следующим образом:

3.4 Спиновое квантовое число 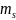характеризует вращение электрона вокруг собственной оси (spin – волчок, юла). Более правильно говорить, что характеризует собственный магнитный момент электрона.

может принимать два значения: = +1/2 (обозначается 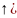и

= -1/2 (обозначается ).

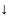Вышеуказанными четырьмя квантовыми числами можно полностью охарактеризовать всю совокупность сложных движений электрона в атоме. Однако заполнение электронами орбиталей происходит не беспорядочно, а в соответствии с определенными принципами.