1. Distance Between a Point and a Plane

Let A be a point and α be a plane. Through A let us draw line d perpendicular to α. Let d intersect plane α at point H. Then the length of line segment AH will be the distance between A and α. Let us show that the length of AH is indeed the shortest distance between A and α.

Let B be another point in α. Then B and H determine a line in α (Figure 1.49). Since d ⊥ α, d ⊥ BH. So AHB is a right triangle with hypotenuse AB.

So AH < AB.

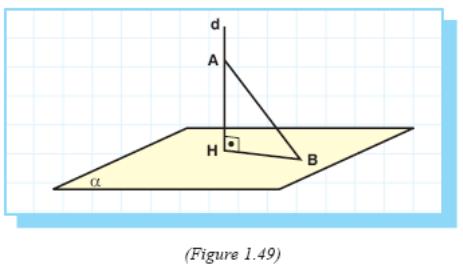
If point A is in α, the distance between A and α is zero.

2. Distance Between a Plane and a Line Parallel to the Plane

Let d be a line parallel to a plane α. Let A and B be two distinct points on d, and m and n be the lines perpendicular to plane α drawn through A and B.

Let m and n intersect plane α at points H and C (Figure 1.50).

So the lengths of line segments AH and BC are the distances from points A and B to α.

Since m and n are parallel, they are coplanar. So A, B, C, H are coplanar points and quadrilateral ABCH is a rectangle. Therefore AH = BC.

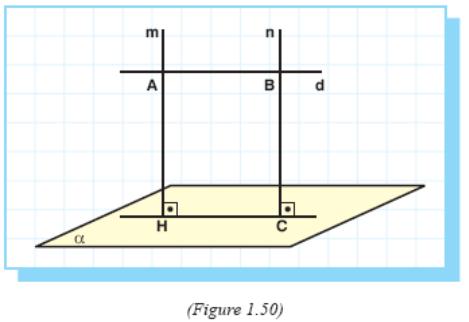
So the distance from every point on line d to plane α is constant. Hence to find the distance between a plane and a line parallel to the plane, we simply find the distance between any point on the line and the plane.

3. Distance Between Two Parallel Planes

Let α and β be two parallel planes. Let A and B be two points in α, and A₁ and B₁ be two points in β so that AA₁ ⊥ β and 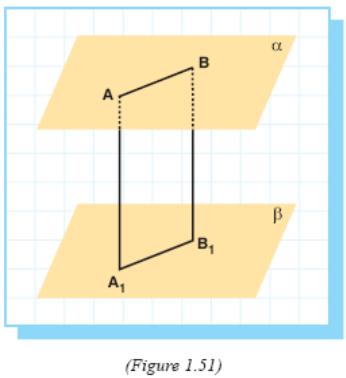BB₁ ⊥ β (Figure 1.51).

Since AA₁ and BB₁ are perpendicular to the same plane they are parallel and determine a plane. When

two parallel planes are intersected by a plane the intersections are parallel. So ABB₁A₁ is a rectangle and AA₁ = BB₁. In other words the distance from any point in one of α or β to the other plane is constant.

To find the distance between two parallel planes, we simply find the distance from any point in any plane to the other plane.

4. Distance Between Skew Lines

To find the distance between two skew lines, we find the distance from one of these lines to the plane containing the other and parallel to the first line. This distance is equal to the length of the line segment perpendicular to both lines. Now let us show this.

Let m and n be two skew lines (Figure 1.52). We proved that we can draw a unique plane parallel to m and containing n. Let α be this plane. Through any point P on m, there can be drawn a unique line perpendicular to α and let Q be the intersection of 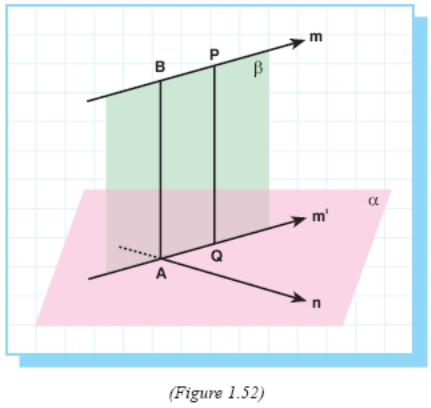this line and α.

Through Q let us draw line m' parallel to m. m' is in α.

Since m // m', they determine a plane β. Let A be the intersection of m' and n.

Through A there can be drawn a unique line

parallel to PQ.

This line will be in plane β. So it intersects line m at a point B.

Since PQ ⊥ α, PQ ⊥ m'. Since m // m' , PQ ⊥ m. So BA ⊥ m.

Since PQ ⊥ α and BA // PQ, BA ⊥ α. So BA ⊥ n. Therefore,

BA is perpendicular to both m and n.

Hence BA is called as common perpendicular of m and n.

Definition (common perpendicular)

The line segment perpendicular to two given skew lines is called as the common perpendicular of the given skew lines.

Theorem: The common perpendicular of two skew lines is unique.

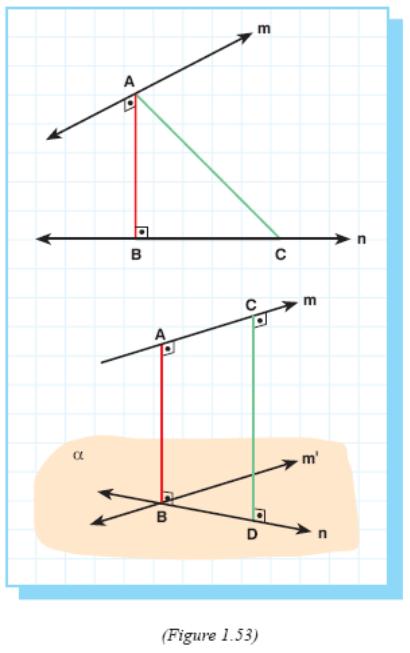
Proof:

Let m and n be two skew lines and AB be

their common perpendicular.

Let C be a point on n (Figure 1.53).

Since ∠ABC = 90°, AC can not be perpendicular to n. So there

can not be drawn any other common perpendicular containing A or B.

Now let us show that there is not any other

common perpendicular except AB.

Assume that CD is a line segment perpendicular to both m and n. Let m' be the line parallel to m and passing through B. Since n and m' are intersecting lines, they determine a plane α.

So AB ⊥ α . Since CD ⊥ m, CD ⊥ m' .

So CD ⊥ α too. Since AB ⊥ α and CD ⊥ α, AB // CD .

Then points A, B, C, D will be coplanar which is impossible.

Hence the common perpendicular is unique

Now, let us show that the length of the common perpendicular is the smallest distance between two skew lines.

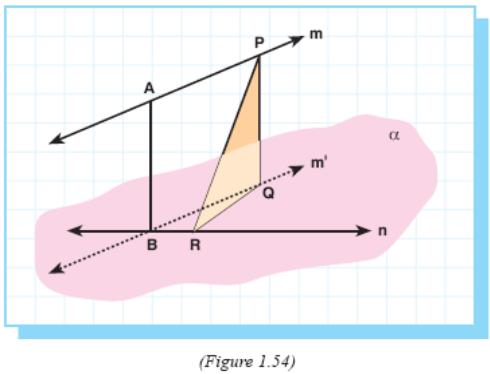
Let m, n be two skew lines and α be the plane containing n and parallel to m. Let AB be the common perpendicular of m and n, and m' be the line passing through B and parallel to m. Let P and R be any two other points on m and n. (Figure 1.54)

Through P let us draw a line parallel to AB and let Q be the intersection of α and this line. Since AB ⊥ α and PQ // AB, PQ ⊥ α.

So, we have that PQBA is a rectangle and AB = PQ .

Since PQ ⊥ α, PQ ⊥ QR. Therefore PR > PQ and since PQ = AB, PR > AB.

So we can conclude that any line segment drawn between two skew lines is longer than their common perpendicular.

(To summarize: the length between two skew lines is the length of the common perpendicular of these lines. This length is equal to the distance from one of them to the plane containing the other and parallel to the first line.)

E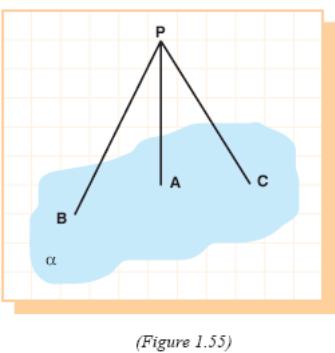 xample 37: From a point P to a plane α, perpendicular PA and two inclined line segments

PB and PC are drawn. Given that,

PB = PC ,

m(∠BPA) = 45°,

m(∠BPC) = 60°, and

PA = 2ñ2 cm, find BC.

S olution:

Since PA ⊥ α, PA ⊥ AB, and since ∠BPA = 45° ,

PB = PA ^.ñ2 = 2ñ2 ^. ñ2 then PB = 4 cm.

Since PB = PC and ∠BPC = 60°,

PBC is an equilateral triangle.

So BC = PB = 4 cm.

Example 38: A line segment AB intersects a plane α at a point C. If and the distance between B and α is 2 cm, find the distance between A and α.

S olution: Let BP ⊥ α and AQ ⊥ α where P, Q are in α.

Then BP // AQ.

They determine a plane β and the intersection of this plane and α is line PQ (Figure 1.57).

Since A and B are in plane β, line AB is in β.

So AB and PQ intersect and this intersection is in α. Since AB intersects α at C, the intersection point is C. So P, C and Q are collinear.

Since PB // AQ, BPC AQC.

So we have .

AQ = 5 ^. BP = 5 ^. 2 = 10 cm.

E xample 39: From a point A to a plane α, perpendicular AB is drawn. If the distance from B to m is 6 cm and AB = 8 cm, find the distance

from A to m. (m is a line in α)

S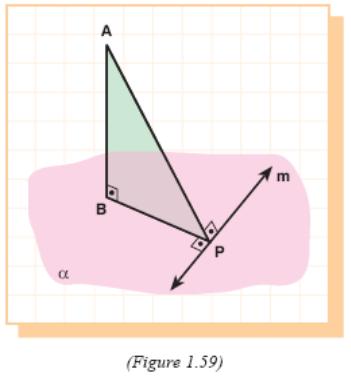 olution: Let BP ⊥m (Figure 1.59). Then BP = 6 cm.

Since AB ⊥ α and BP ⊥ m, by the three perpendiculars theorem, AP ⊥ m.

So the distance from A to m is AP.

Since AB ⊥ α, AB ⊥ BP.

So .

Example 40: ABCD is a rhombus and P is a point not in (ABC) so that

PA ⊥ (ABC). Find the distance between lines PC and BD if PA = AB = 4 cm and ∠DAB = 60° .

S olution: Let M be the intersection point of diagonals AC and DB.

Let MN be perpendicular to PC.

Let us show that MN ⊥ DB too.

Since PA ⊥ (ABC) , PA ⊥ AB and PA ⊥ AD.

Since AD = AB and ∠PAB = ∠PAD,

PAB  PAD (S.A.S.)

So PD = PB.

Since PD = PB and DC = BC , PDC  PBC (S.S.S.).

So ∠NCD = ∠NCB.

Then NCD  NCB (S.A.S.).

So ND = NB, DM = MB, and NDM  NBM (S.S.S.).

Thus we get ∠NMD = ∠NMB = 90°.

Hence NM is the common perpendicular of DB and PC.

So the distance between PC and DB is the length of MN.

Now let us find MN.

∠DAB = 60° , AB = 4 cm, and PA = 4 cm are given. Then AM = 2ñ3 cm and

MC = 2ñ3 cm.

Since PA ⊥ (ABC), PA ⊥ AC. Then , CMN CPA

(A.A.A.)

So , , cm.

Example 41: Side AB of triangle ABC is in a plane α. Find the distance from

C to α if the distance from the centroid to α is 2 cm.

Solution: L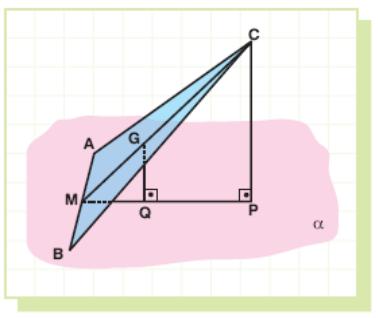 et G be the centroid of ABC,

GQ ⊥ α, and CP ⊥ α (Q and P are in α).

Let M be the midpoint of AB.

C, G, M are collinear.

Since GQ ⊥ α and CP ⊥ α, GQ and CP are

in the same plane.

Since G and C are in this plane, M is also in

this plane.

Since M, Q, P are intersections of this plane and α, they are on the same line.

Then GQ // CP and MGQ MCP.

So . GQ = 2 cm is given. So CP = 6 cm.

Example 42: m and n are two lines parallel to a plane α and they are on the same side of α. If the distances from m and n to α are equal, can m and n be skew lines?

S olution:

Let A and B be points on m and n respectively.

Let A₁ and B₁ be two points in α such that

BB₁ ⊥ α and AA₁ ⊥ α.

Given that m and n are equidistant from α.

So AA₁ = BB₁.

Since AA₁ ⊥ α and BB₁ ⊥ α, AA₁ ⊥ B₁A₁ and

BB₁ ⊥ B₁A₁.

Moreover BB₁ // AA₁. So AA₁B₁B is a rectangle. So AB // A₁B₁.

Then AB and m determine a plane parallel to α.

Through B there can be drawn only one plane parallel to α.

So n is in the plane determined by m and AB.

Therefore m and n are coplanar. So they cannot be skew lines.

Example 43: A, B, C are three points in a plane α and M is a point not in α so that MB ⊥ α. If MB = 3 cm, ∠MAB = 60°, and ∠MCB = 45°, what is the maximum length of line segment AC in cm?

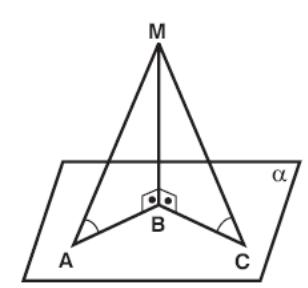
Solution: Since MB⊥ α, MB⊥AB and MB⊥BC.

MB = 3 cm, ∠MAB= 60°, ∠MCB = 45 are given.

So AB = ñ3 cm and BC = 3 cm.

AC is maximum if A, B, C are collinear.

Because if they are noncollinear in ABC AC < AB + BC.

So the maximum length is AB + BC = 3 + ñ3 cm.

Example 44: ABC is an equilateral triangle with a side of 1 cm. M is a point not in (ABC). If MB ⊥ (ABC), what is the distance between lines MB and AC in cm?

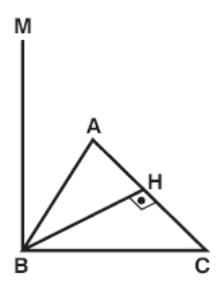
Solution: Let BH ⊥ AC.

Since MB ⊥ (ABC), MB ⊥ BH.

So BH is the common perpendicular of MB and AC.

ABC is an equilateral triangle.

So BH = cm is the distance between the lines MB and AC.

Example 45: ABCD is a square and MA ⊥ (ABC). If MA = 2AB,

what is cos ∠BMC?

S olution: Let AB = a.

Then MA = 2a and AC = añ2.

Since MA ⊥ (ABC), MA ⊥ AB and MA ⊥ AC.

Then and

.

Since MA ⊥ (ABC) and AB ⊥ BC by three perpendiculars theorem MB ⊥ BC.

So, .

Example 46: In the adjacent figure, DA ⊥ (ABC).

If m(∠ABD) = m(∠ADC) = 60° and m(∠BDC) = 45°.

What is cos (∠BAC) ?

Solution:

Since DA ⊥ (ABC), DA ⊥ AB and DA ⊥ AC.

Let AB = a.

Then AD = añ3, DB = 2a, AC = ñ3 ^. AD = 3a, DC = 2AD = 2añ3.

Then in BDC by cosine thorem:

In ABC by cosine theorem:

Equalizing these two equations gives us: .

S o, and .

Example 47: In the figure, ABCD is a square, O is the center of ABCD and PO ⊥ (ABC).

Given that, AB = 6 cm and PO = 4 cm.

What is the distance between lines AD and PC?

Solution: Since AD//BC, AD//(PBC).

So we need to find the distance from AD to (PBC).

Since PO ⊥ (ABC) PO ⊥ OB, PO ⊥ PC.

Then and .

Since OB = OC, PB = PC.

Let E be the midpoint of BC.

Since PB = PC, PE ⊥ BC.

Then draw EO. Let EO intersect AD at F.

Since EB = EC and O is the center of ABCD then EF//AB. So BC ⊥ EF.

BC ⊥ EF, BC ⊥ PE. So BC ⊥ (PFE).

Let FH ⊥ PE. Since BC ⊥ (PFE) then BC ⊥ FH.

FH ⊥ BC, FH ⊥ PE. So FH ⊥(PCB).

Therefore the distance from AD to (ABC) is FH. Now let us find FH.

cm.

cm.

Check Yourself 11

1 . A and B are two points equidistant from a plane α and they are on the same side of α. Show that AB // α.

2. In the adjacent figure, PQ is a line segment on one

side of α. If the distances from P and Q to α are 4

cm and 6 cm respectively, find the distance from the

midpoint of PQ to α.

3 . ABC is a triangle on one side of a plane α.

If the distances from vertices A, B, and C to α are 6 cm,

8 cm, and 10 cm respectively, find the distance

from the centroid of ABC to plane α.

4. ABCD is a rhombus and PA ⊥(ABC). If ∠BAD = 60° and AC = 2ñ3, find the distance between lines PA and BC.

5. m and n are two lines parallel to a plane α and they are on the same side of α. If the distances from m and n to α are equal, can m and n be skew lines?

Answers

2. 5 3. 8 4.

5. No. They are intersecting, coincident or parallel lines.

EXERCISES 2

A. Perpendicular Lines

1. State the following as true or false.

a. From a point on a line in the plane we can draw only one line perpendicular to that line.

b. From a point on a line in the space we can draw only one line perpendicular to that line.

c. If a line is perpendicular to another line in space we can find a line d which is perpendicular to both of the lines.

2. d, k and l are three different lines in space. State the following as possible or impossible.

a. d // k, d l, k l.

b. d k, k l, d l

c. d // k, k // l, d l

d. d // k, d l,

3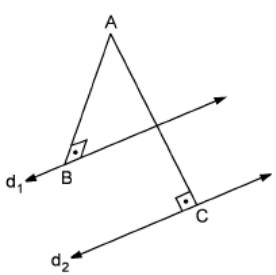 . In the figure the lines d₁ and d₂ are parallel to each other. Given that AB d₁, AC d₂, AB = 5 cm and AC = 13 cm. If the distance between d₁ and d₂ is 12 cm find the angle <ABC.

B. Line Perpendicular to a Plane

4. A nd B are two points in the space. Distances between A, B and a plane P are 8 cm and 4 cm, respectively. The distance between their intersection points with the plane P is 9 cm. Find the distance between A and B if;

a) A and B are in the same side of the plane.

b) A and B are in opposite sides of the plane.

5 . In the adjacent figure, in plane α there is a circle and a line m tangent to the circle at a point T.

A is a point on circle such that PA ⊥ α where P is not in α.

If PT ⊥ m, PT = 10 cm, and PA = 8 cm, find the radius of the circle.

6 . In the figure E is a plane, d is a line in E and the circle with center O is in E. From a point A outside of plane E we draw a perpendicular line AO to plane E. Given that, d is tangent to circle at B, BC = 8 cm, radius of circle is 6 cm and AO = 24 cm.

Find AC.

7. There is a circle in a plane. AB is the diameter of the circle. From point A we draw perpendicular line PA, to the plane. Given that PA = 5 cm and the radius of the cirle is 6 cm. Find the distance between the point P and the farrest point of the circle.

8 . In the adjacent figure, PG is perpendicular to

the plane of equilateral triangle ABC at its centroid G.

If m(∠AFP) = 45°, what is

?

9. In the figure DBC is an isosceles right triangle in the plane E. AD is perpendicular to plane E. Given that BD = 6 cm and ABC is an equilateral triangle. Find AD.

1 0. In the adjacent figure, PA ⊥ (ABC).

If m(∠APB) = m(∠APC) = 45° and

m(∠BPC) = 60°, find m(∠BAC).

11. Show that if two planes are perpendicular to the same line then these planes are parallel.

1 2. In the figure line CD is perpendicular to plane E. Given that AO = BO and C. Prove that ABC is an isosceles triangle.

13. State the following as true or false.

a. If a line is perpendicular to any line in a plane then it is perpendicular to the plane.

b. From any point of a line we can draw only one perpendicular to this line in space and in plane.

c. In plane P there are two lines d and l. All lines which are perpendicular to both of d and l are perpendicular to plane P.

1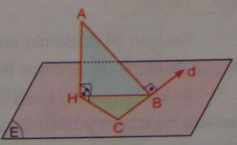 4. In the figure, AH is perpendicular to plane E. d is a line in plane E and AB  d. Given that AB = 10 cm and AH = 7 cm. What is the smallest integer value of HC.

15. A triangle ABC is given in space. What is the set of all points which are equidistant from the vertices of the triangle.

1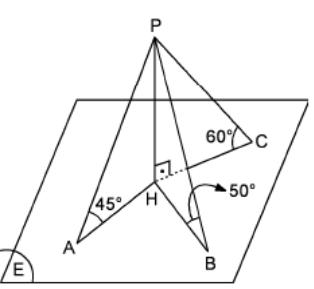 6. In the figure PH E. Given that

m(<PAH) = 45,

m(<PBH) = 50,

m(<PCH) = 60.

State the following as true or false.

a. PA > PB

b. PA < PC

c. PH = AH

d. PH > CH

e. PB < PC

f. AH > BH

g. HB > HC

17. In the figure PH is perpendicular to plane E. Given that PA > PB > PC. How do we order AH, BH and CH?

1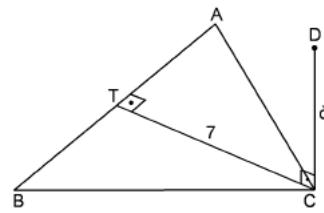 8. In the figure ABC is an isosceles triangle with CT = 7 cm, AB = 14 cm, AC = BC. Given that CD is perpendicular to the plane of ABC. If CD = 6 cm find DB.

19. In a plane there are two parallel lines d and k. A and B are two points on line d and AB = 6 cm. If the distance between these two lines is 5 cm find the area of ABC where C is a point on line k.

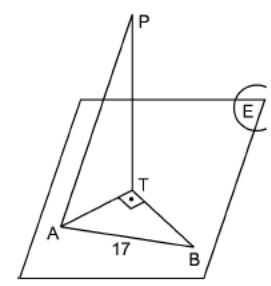
20. In the figure PT is perpendicular to plane E. ATB is a right triangle with AB = 17 cm. If PA = 25 cm and PT = 24 cm find BT.

2 1. In the figure ABCD is a rectangle with sides AB = 10 cm and BC = cm. Given that,

KD (ABCD) and

KD = 5 cm.

Find the area of ACK.

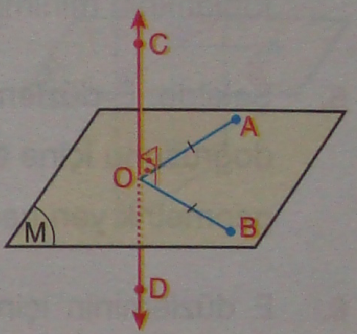
22. In the figure the line CD is perpendicular to plane M at point O. Given that OA = BO. Prove that ABC is isosceles triangle.

2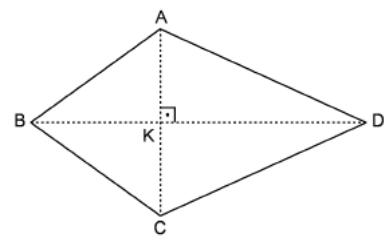 3. In the figure ABCD is a kite. We draw a line PD perpendicular to the plane of ABCD. Given that,

AB = 13 cm,

BK = 12 cm,

KD = 24 cm and

PD = 7 cm.

Find A(ACP).

24. Two airplains with the same velocity are flying from the same plane at the same time. They make a 60 and 45 angles with the plane, respectively. When they collide they have 9000 m height. What was the distance between them initially?

2 5. In the figure AP and BQ are perpendicular to plane E. C is a point on PQ. Given that,

AP = 16 cm,

BQ = 8 cm and

PQ = 18 cm.

What is the minimum value of AC + BC.

C. Perpendicular Planes

26. Show that through a given point A, there can be drawn infinitely many planes perpendicular to a given plane α.

2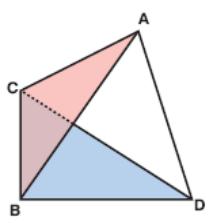 7. In the adjacent figure, ABC is an equilateral triangle and BDC is an isosceles triangle.

AB = 6 cm and BD = DC = 5 cm are given.

Find AD, if (ABC) ⊥ (BDC).

28. Two planes are perpendicular to each other. Can we draw a line,

a) Perpendicular to both of the planes

b) Parallel to both of the planes

c) Perpendicular to one of the planes and parallel to other plane.

2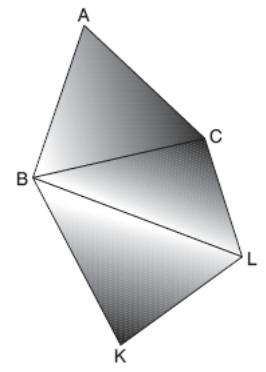 9. In the figure ABC, BCL and BKL are equilateral triangles. Given that (ABC) is perpendicular to (BCL) and (BCL) is perpendicular to (BKL).

If AB = 4 cm find AK.

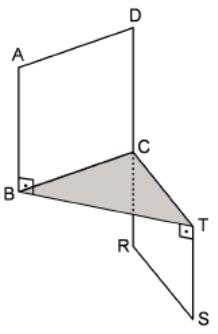
30. In the figure ABCD and CRST are two congruent squares.

Given that AB is perpendicular to BT, BT is perpendicular to TS and BT = TS = 6 cm. Find AS.

3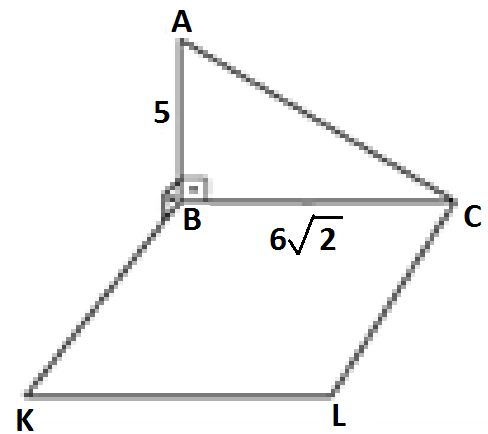 1. In the figure ABC is a right triangle and BCLK is a square. Given that AB is perpendicular to BK, AB = 5 cm and BC = cm. Find AK + AL.

32. State the following as true or false.

a. Three planes may be perpendicular to each other.

b. Three lines may be perpendicular to each other.

c. A line may be parallel to both of two intersecting planes.

d. A line may be perpendicular to both of two intersecting planes.

33. State the following as true or false for a space.

a. There are infinitely many planes perpendicular to a line.

b. There are infinitely many lines perpendicular to a line.

c. From a point we can draw only one perpendicular plane to a line.

d. From a point we can draw only one perpendicular line to a line.

e. We can draw infinitely many perpendicular lines to a line.

3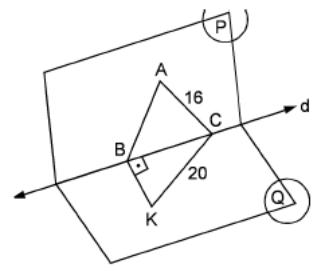 4. In the figure the planes P and Q are perpendicular to each other and their intersection is the line d.

Given that ABC is an equilateral triangle,

m(<KBC) = 90,

KC = 20 cm and

AC = 16 cm.

Find AK.

3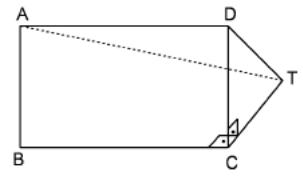 5. In the figure ABCD is a rectangle; DCT is an isosceles right triangle. Given that,

TC (ABCD)

AD = 8 cm,

AB = 6 cm.

Find AT.

36. In the figure, ABCD and ADEF are rectangles. Given that, ED DC,

A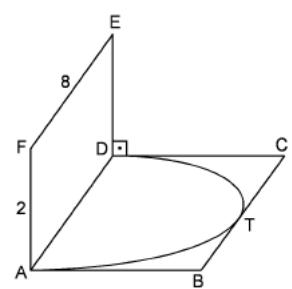 D = 2 cm,

EF = 8 cm.

The semicircle that we draw inside of ABCD is tangent to BC at T. Find FT.

3 7. In the figure ABCD is a rectangle and CDKL is a square. Given that,

BC CL,

AD = cm and

DK = 5 cm.

Find AL.

D. Distance

3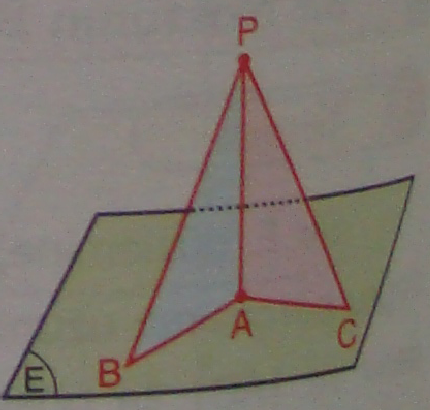 8. In the figure E is a plane and P is a point outside of P. We draw aperpendicular line PA to the plane P. Prove that ,

a) If AB = AC then PB = PC.

b) If PB < PC then AB < AC.

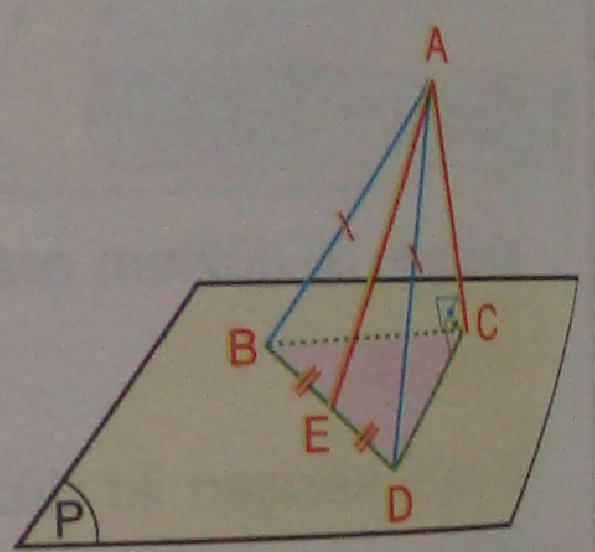
39. In the figure AC is perpendicular to plane P. Given that, m( CAE) = 30,

BE = ED = 5 cm,

AB = AD and

DC = 13 cm.

Find A(ABD).

4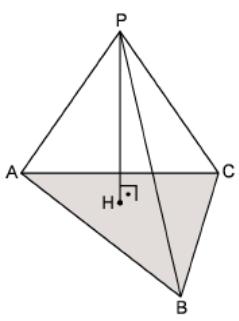 0. In the figure PH is perpendicular to the plane and PB = 5 cm. Given that H is the center of circumcircle of ABC.

Find PA + PC.

41. An ant is walking 5 m to east then 2 m to south. Then it is climbing on a plane with a 60 inclination for 4 m to the west. What is the distance between the starting point and the end point of the ant.

42. A helicopter is rising for 600 m then going to east for 800 m then to north for 2400 m. What is the distance between the starting and ending point of the helicopter?

4 3. In the figure line k is parallel to plane P and line t is in P. Distance between k and t is 24 cm. If AR = 7 cm find BR.

44. In a plane there are two parallel lines d and k. A and B are two points on line d and AB = 6 cm. If the distance between these two lines is 5 cm find the area of the triangle ABC where C is a point on line k.