2. Perpendicularity

In this section we will learn the perpendicular lines, conditions of being perpendicular, the lines which are perpendicular to a plane and perpendicular planes. After that we will learn finding and using the distances in space.

A. PERPENDICULAR LINES

Definition: (perpendicular lines)

Two lines a and b are perpendicular to each other if the angle between them is 90°.

For intersecting lines we can easily define the perpendicularity. But, if the lines are skew lines then we will take any point on one of the lines and draw a parallel line to the other line. If the angle between these two intersecting lines is 90° then the given skew lines are said to be perpendicular.

Theorem: If one of two parallel lines is perpendicular to a third line, the other is perpendicular too.

Proof:

L et m and b be two parallel lines and m be perpendicular to c (Figure 1.36).

Through any point A, let us draw lines m₁ and c₁ so that m₁ // m and c₁ // c.

Since m ⊥ c, the angle between m₁ and c₁ is 90°.

On the other hand, since m₁ // m and m // b, we get m₁ // b.

So the angle between b and c is also 90°.

That means b and c are perpendicular lines

Example 26: By using perpendicularity, prove that if two lines are parallel to the same line they are parallel.

S olution: Let m, n and d be three lines. Let

m // n and d // n. We need to prove that m // d.

Let A be a point on n. We can draw a plane α perpendicular to n at A. So n ⊥ α.

Since m // n and n ⊥ α, m ⊥ α because of the previous theorem.

Since d // n and n ⊥ α then d ⊥ α .

Since m and d are perpendicular to α by using the previous theorem they are parallel.

Check Yourself 8

1. State the followings as true or false.

a. Two lines d and k are parallel to the same plane. If a line l is perpendicular to line d it must be always perpendicular to line k.

b. Two perpendicular lines are given in space. If a line is perpendicular to these lines at their intersection point then this line is perpendicular to the plane, which includes the perpendicular lines.

c. Given that d, k and l are three lines in space. If d and k are perpendicular to line l they must be parallel to each other.

d. Two lines d and k in a plane are perpendicular to the same line l. Another line m is parallel to line l then m is perpendicular to d and k, also.

Answers

1. a) False b) True c) False d) True

B. LINE PERPENDICULAR TO A PLANE

Definition: (line perpendicular to a plane)

A line is said to be perpendicular to a plane if it is perpendicular to every line in this plane.

Let us say that m is a line and α is a plane. If it is given that m  α then m is perpendicular to any line in α.

If m  α then m intersects α. To prove this statement let us assume that m does not intersect α.

In this case there are two possibilities for m and α :

1. m is in α. Then since it is not perpendicular to a line in α, that is itself, m is not perpendicular to α.

2. m is parallel to α. In this case in α there can be found a line parallel to m. So m can not be perpendicular to α.

In both conditions m is not perpendicular to α.

Therefore, m intersects α.

Definition: (inclined line)

If a line intersects a plane but not perpendicular to the plane it is called an inclined line.

Theorems:

1. If a line is perpendicular to two intersecting lines lying in a plane then it is perpendicular to the plane.

2. Through any given point in space, there can be drawn one and only one plane perpendicular to a given line.

3. If one of two parallel lines is perpendicular to a plane then the other line is also perpendicular to the same plane.

4. Two lines perpendicular to the same plane are parallel.

5. Through a point in space, there can be drawn only one line perpendicular to a given plane.

6. If a line is perpendicular to one of two parallel planes, it is perpendicular to the other.

Proofs:

1. We need to prove that if a line is perpendicular to two intersecting lines in a plane it is perpendicular to any line in this plane.

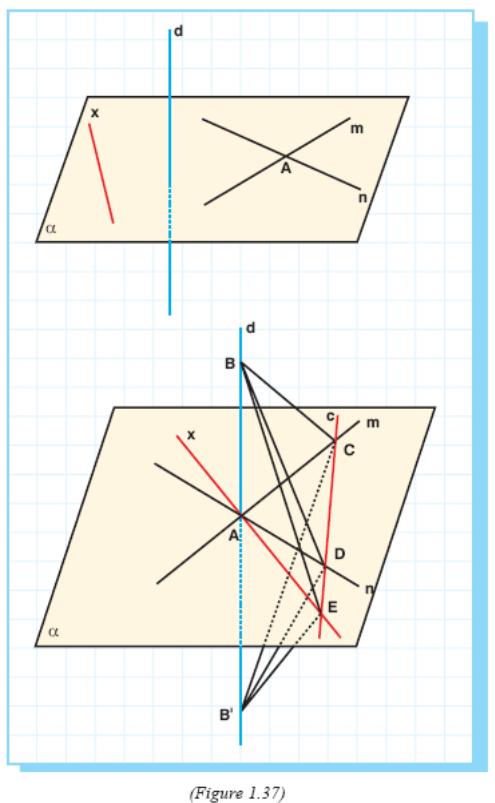
Let d be a line perpendicular to two lines m and n lying in α. Let A be the intersection point of m and n.

It is obvious that d is perpendicular to every line in α which is parallel to either one of m or n (Figure 1.37).

So we should check for the lines which are not parallel to neither m nor n.

Let x be any line intersecting both m and n.

We have to prove that d is perpendicular to x too.

Let us shift lines d and x so that A is on d and x.

Let c be any line in α intersecting m, n, x at

points C, D, E respectively.

On line d let us take two points B and B' so that BA = B'A.

Then BAC and B'AC are congruent, similarly BAD and B'AD are congruent (by S.A.S.).

So BD = B'D and BC = B'C.

Then BDC and B'DC are congruent (by S.S.S.). That means ∠BDC = ∠B'DC.

Then BDE and B'DE are congruent triangles (by S.A.S.).

So BE = B'E and BAE and B'AE are congruent (by S.S.S.).

Hence ∠BAE = ∠B'AE = 90°.

So d is perpendicular to x.

Therefore d is perpendicular to any line in α. So d ⊥ α.

2 . We have two cases: