6. Determination of a Space

By using different ways we can define a space. Now, let us define these ways.

Rule: We can define a space by:

1. Four non-coplanar points.

2. Two parallel planes.

3. Two intersecting planes.

4. Two skew lines.

Check Yourself 6

1. State the following as true or false.

a. If a plane is parallel to the plane that we obtain by two parallel lines then this plane is parallel to these lines too.

b. Two planes are parallel to each other. Another plane intersects these planes. The intersections of parallel planes and third plane are intersects at one point.

c. By using two parallel lines we obtain a plane. By using another two parallel lines we obtain another plane. If these two planes are parallel to each other then all these four lines must be parallel to each other.

2. Two parallel planes are intersected by a third plane. What can we say about the intersections of parallel planes and third plane?

3. Can we draw a line parallel to three planes that are:

a) intersected at a line?

b) intersected at three lines?

c) intersected at a point?

d) coincident?

e) parallel to each other?

Explain your answer.

4. State the followings as true or false.

a. Four non-collinear points determine a space.

b. Two intersecting lines and another line perpendicular to these intersecting lines determine a space.

c. Three lines which are perpendicular to each other determine a space.

d. Three parallel lines in space always determine a space.

e. A plane and a point outside of this plane determine a space.

Answers

1. a) T b) F c) F

2. They are two parallel lines.

3. a) Yes b) Yes c) No d) Yes e) Yes

4. a) F b) T c) T d) F e) T

C. THALES THEOREM IN SPACE

We know from the plane geometry that the Thales Theorem is related with parallel lines. Now, we will write the same theorem for parallel planes.

Theorem: If two lines are intersected by parallel planes, the line segments

between the planes are proportional.

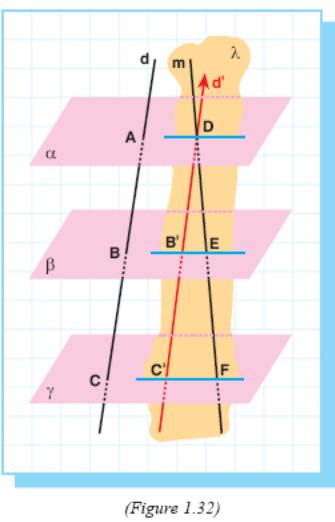
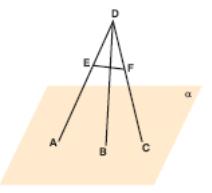
Proof: Let α, β,  be three planes (Figure 1.32).

Let d be a line intersecting α at A, β at B and  at C, and m be another line intersecting α, β,  at points D, E and F respectively.

We need to prove, .

Through point D there can be drawn line d' parallel to line d.

Since d intersects β and , d' also intersects these planes.

Let B' and C' be the intersection points.

Since α, β and  are parallel, and d and d' are parallel, AB = DB', BC = B'C'. (I)

Lines m and d' are intersecting lines. So they determine a plane λ.

Since β and  are parallel planes, the intersection of λ and β is parallel to the intersection of λ and β.

So B'E // C'F, and DB'E and DC'F are similar triangles.

So (II)

From (I) and (II), .

E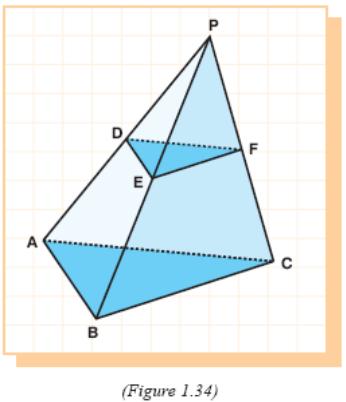 xample 22: In the figure, planes DEF

and ABC are parallel.

If PF = 2 cm,

FC = 4 cm, and

A(DEF) = 3 cm² ,

find the area of ABC.

Solution:

Lines PB and PC are intersecting lines.

So they determine a plane.

Since (DEF) and (ABC) are parallel planes which are intersected by plane BPC, the intersections will be parallel.

So EF // BC, and PEF and PBC are similar.

So . (I)

Similarly it can be obtained that PDF PAC and PDE PAB.

So (II) and (III)

From (I), (II), and (III), , DEF and ABC are similar triangles.

Hence and A(ABC) = 27 cm² .

Example 23: In the figure α and β are

parallel planes. A plane parallel to α is intersecting

AB at P and CD at Q.

If AP = 2 cm,

AB = 8 cm, and

QD = 9 cm, find CQ.

Solution:

By the Thales theorem,

Then and CQ = 3 cm.

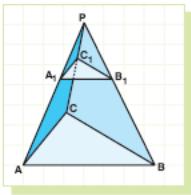
Example 24: In figure P is not in (ABC).

If and A₁C₁ // AC then show that

(A₁B₁C₁) // (ABC).

Solution:

Since A₁C₁ // AC, PA₁C₁ and PAC are similar triangles.

So (I).

It is given that (II).

From (I) and (II), we get .

So PC₁B₁ and PCB are similar.

So C₁B₁ // CB.

Then two intersecting lines in (ABC) (which are AC and CB) are parallel to two intersecting lines in (A₁B₁C₁).

Therefore, (A₁B₁C₁) // (ABC).

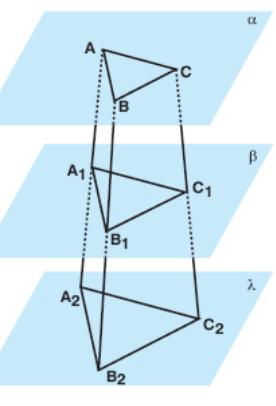
Example 25: In the adjacent figure, α // β // λ. Moreover AB // A₁B₁, BC // B₁C₁, AC // A₁C₁.

Find the perimeter of A₂B₂C₂ if the perimeters of

ABC and A₁B₁C₁ are 6 cm and 9 cm, respectively, and .

Solution:

Since AB // A₁B₁ they determine the plane (ABB₁), since BC // B₁C₁ they determine the plane (BCC₁) and since AC // A₁C₁ they determine the plane (ACC₁).

A₂B₂ is the intersection of (ABB₁) and (A₂B₂C₂).

Since (A₁B₁C₁) // (A₂B₂C₂) A₁B₁ // A₂B₂.

By the same logic B₁C₁ // B₂C₂ and A₁C₁ // A₂C₂.

Since AB // A₁B₁ and BC // B₁C₁, ∠ABC = ∠A₁B₁C₁.

Since BC // B₁C₁ and AC//A₁C₁, ∠BCA = ∠B₁C₁A₁. So ABC A₁B₁C₁.

BB₁ and CC₁ cannot be parallel lines. Because if they are parallel then BCC₁B₁ will be a parallelogram and BC will be equal to B₁C₁.

However in this case triangles ABC and A₁B₁C₁ will be congruent and their perimeters will be equal. But by givens they are not equal.

Hence BB₁ is not parallel to CC₁. By the same logic AA₁ /\/ BB₁, AA₁ /\/CC₁. Then BB₁ and CC₁ are intersecting lines. Let P be the intersection point.

We learned that when three planes intersect each other if two of three of intersection lines intersect each other at a point the third intersects them at the same point. So AA₁ passes through P.

PBC PB₁C₁. So . So if BB₁ = 3x, PB = 6x.

is given so B₁B₂ = 5x. Then .

PBC PB₂C₂. Then ,

P(A₂B₂C₂) = 14 cm.

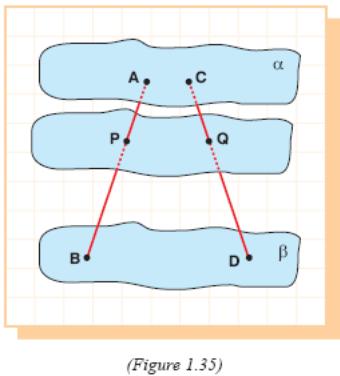
Check Yourself 7

1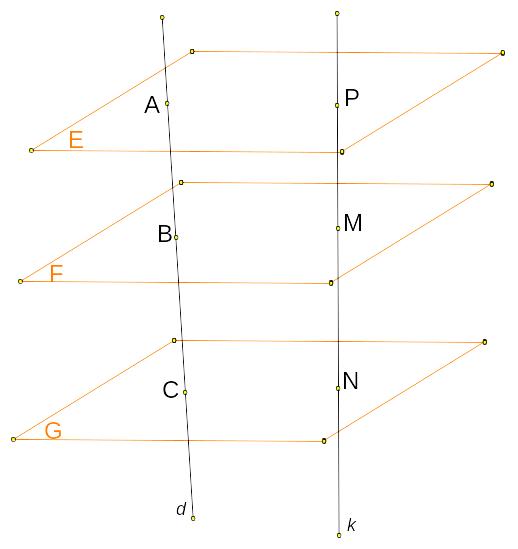 . In the figure E, F and G are three parallel planes in space.

The lines d and k intersect these planes at the points A, B, C and P, M, N. Given that

AB = 10 cm,

AC = 16 cm

MN = 12 cm.

Find the length of PM.

2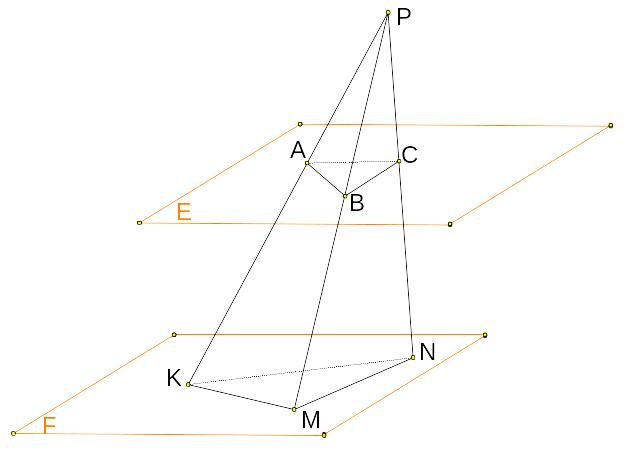 . In the figure the planes E and F are parallel to each other. PK, PM and PN are three lines intersecting both of the planes. Given that

PA = AK,

BC = 6 cm,

AC = 7 cm and

KM = 20 cm.

Find the perimeters of ABC and KMN.

Answers

1. 20 cm 2. P(ABC) = 23 cm, P(KMN) = 46 cm.

EXERCISES 1

A. Axioms of Space Geometry

1. In figure, A, B, C are non-collinear points,

E and F are on DA and DC respectively.

Can EF intersect DB?

2. α and β are two intersecting planes. In α there is a line m intersecting β at point A and in β there is a line n intersecting α at point B where A and B are distinct points.

Show that α and β intersect along line AB.

3. Given that points A₁, A₂, A₃..., A₂₅ determine only one plane. At most how many of these points can be collinear?

4. A line d and a point A outside of this line are given in space. How many parallel lines can we draw from A to d?

B. Lines and Planes in Space

5. By using a triangle and a point outside of this triangle at most how many planes can we determine?

6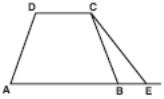 . In figure, AB // CD, points A, B and E are collinear. Show that all points in the figure are coplanar.

7. m, n and d are three lines in space such that m and n are intersecting at point A, and n and d are intersecting at point B.

Do m, n, d always lie in the same plane?

8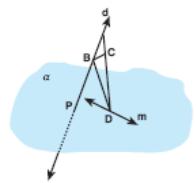 . In the adjacent figure, m lies in α and d intersects α at point P which is not on m.

Show that BC and m are skew lines.

9. Which of the following are correct?

a. Two parallel lines determine a plane.

b. Two skew lines do not determine a plane.

c. A line and a point, outside of this line do not determine a plane.

d. Two points in a plane and another point outside of this plane define a plane.

e. Three non-collinear points determine a plane.

f. A line and a point, outside of this line determine a plane.

10. We take 4 points in a plane and one line outside of this plane. By using these 4 points and one line at most how many planes can we draw?

1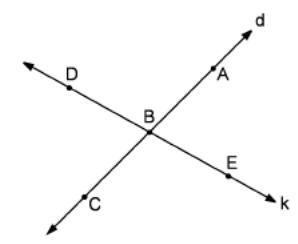 1. In the figure d k = B. By using these points how many different planes can we draw?

12. Five different lines are intersecting at the same point in space. By using them at most how many planes can we draw?

13. ABC is a triangle and P is a point not in (ABC). Show that the line joining the midpoints of PC and AB and the line joining the midpoints of PA and CB are intersecting lines.

14. Show that there can be drawn a unique plane containing one of two given skew lines and parallel to the other line.

15. ABCD is a parallelogram, and A₁, B₁, C₁, D₁ are four coplanar points not in (ABC). Show that if A₁, B₁, C₁, D₁ are on the same side of (ABC) and

AA₁ // BB₁ // CC₁ // DD₁, then AA₁ + CC₁ = BB₁ + DD₁ .

16. At which condition and for at least how many common points can two planes become coincident?

17. Five points of two planes are common. Can we say that these two planes are coincident? Why?

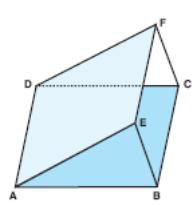
18. In the adjacent figure, ABCD and AEFD are

parallelograms. Show that EAB and FDC are

congruent triangles.

1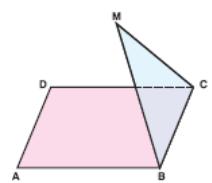 9. In the adjacent figure, ABCD is a parallelogram.

M is not in (ABC).

Show that AD // (MBC).

20. m and n are two parallel lines not lying in a plane α. Show that if m // α, line n is parallel to α, too.

21. m and n are skew lines. Show that there can be drawn two parallel planes α and β such that α contains m and β contains n, and show that these α and β are unique.

22. Two skew lines are given. What can we say about the planes that include these skew lines?

2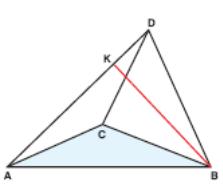 3. In the adjacent figure, D is not in (ABC).

AC = AB, DC = DB, and BK ⊥ DA .

If KD = 3 cm and DB = 6 cm, find KC.

24. Which of the following are correct for two lines in a space?

a) If two lines are skew they don’t intersect.

b) If two lines are in the same plane they are intersected.

c) If two lines are non-coplanar they don’t intersect.

d) It two lines are parallel they are coplanar.

e) If two lines intersect their intersection is a unique point.

f) If 2 lines don’t intersect they are parallel.

25. Which of the following are correct for three lines in a space?

a) 3 distinct lines divide a plane into at least 4 regions.

b) 3 lines divide a plane into at least 2 regions.

c) 3 lines may be perpendicular to each other at one common point.

d) 3 lines may intersect at one point.

2 6. In the adjacent figure, ABC

and BCD are equilateral.

If ∠ACD = 20° find ∠BDA.

27. ABC and A₁B₁C₁ are two triangles in two parallel planes.

If AA₁ // BB₁ // CC₁ then show that ABC and A₁B₁C₁ are congruent triangles.

28. Line m is parallel to α and intersects plane β. Show that α and β are intersecting planes.

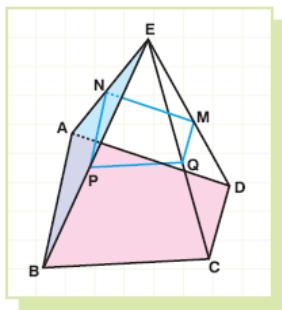
29. Trapezoid ABCD (AB // CD) and triangle ABE have a common side AB and lie in distinct planes.

M, N, P, Q are the midpoints of ED, EA, EB and EC, respectively.

What kind of quadrangle is MNPQ?

30. Show that for four non-coplanar points A, B, C, D three of them cannot be collinear.

31. State the following expressions as true or false for a space.

a) If two lines are not skew then they are parallel.

b) We can draw only one perpendicular to a line from a point on that line.

c) From a point outside of a line we can draw more than one parallel line to given line.

d) There different lines may be perpendicular to each other.

e) We can draw only one parallel line to plane from a point outside of that plane.

32. Which of the following is/are correct?

a. In space two lines may intersect at one point.

b. If two planes in space are parallel then all lines on these planes are parallel to each other.

c. In plane two lines are parallel to each other. If another line is perpendicular to one of these lines it must be parallel to other line.

33. 6 collinear and 5 non-collinear points are given in space. At most how many planes can we determine by using these points?

34. How many lines can we draw by using 7 non-collinear points, in space?

35. How many planes can we draw from 9 non-coplanar points?

36. Check as true or false:

a. A line in space intersects one of two parallel lines then it must intersect second line too.

b. A line in plane intersects one of two parallel lines in the same plane then it must intersect second line too.

c. A line d and a point A outside of this line are given in space. We can draw infinitely many parallel lines from A to line d.

37. Four rays AB, AC, PQ and PR are given in space. Given that AB // PQ and AC // PR. We take four points K, L, M and T on the rays AB, AC, PR and PQ, respectively. Given that AK = PT, AL = PM. What are the shapes of the quadrilaterals AKTP and KLMT?

38. From one vertex of aparallelepipedwe draw three diagonals. From the endpoints and the midpoints of these diagonals we draw two planes P and Q. Prove that P and Q are parallel to each other.

(Answer: Hint: Use theorem 1 in mutual positions of a plane and a line)

39. P and Q are two parallel planes. ABCD is a quadrilateral in P. We draw parallel lines from the vertices of ABCD to plane Q and we get the quadrilateral A₁B₁C₁D₁. Prove that the quadrilaterals ABCD and A₁B₁C₁D₁ are congruent to each other.

40. ABCD is a tetrahedron. M, N and P are the midpoints of AB, AC and AD, respectively. What can we say about the planes including BCD and MNP?

41. P and Q are two planes in space. Prove that any plane in that space intersects at least one of P and Q.

42. Two skew lines in space are given. Prove that from a point outside of these lines we can draw unique plane parallel to both of the lines.

43. In space how many lines can we draw which are equidistant from three points?

44. ABC is a triangle and EF is its median which is parallel to BC. A plane P istersects ABC in the line EF. Prove that the line BC is parallel to plane P.

C. The Thales Theorem in Space

45. In the figure the planes R and S are parallel to each other. Given that,

A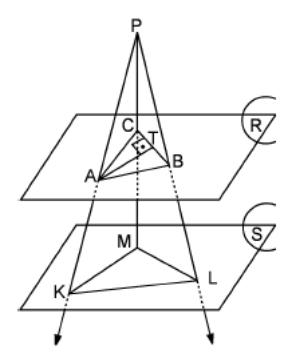 B = 4 cm,

BC = 4 cm,

KL = 8 cm and

AT = 3 cm.

Find the area of KLM.

4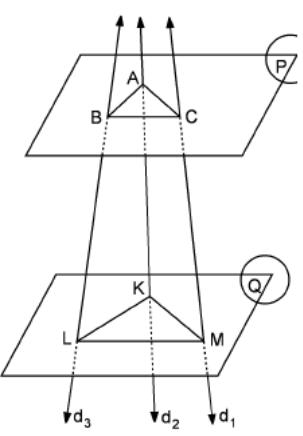 6. In the figure the planes P and Q are parallel to each other. The lines d₁, d₂ and d₃ cut these planes by 60 angles and intersect at point S outside of these planes. The triangles ABC and KLM are equilateral triangles with side lengths 4 cm and 8 cm.

Find the ratio .

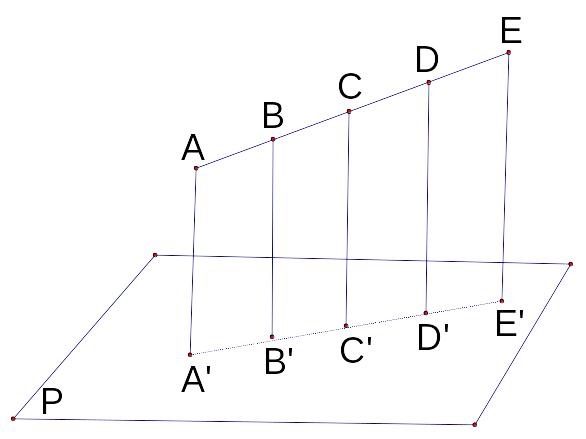
47. In the figure AA’ // BB’ // CC’ // DD’ // EE’ and AA’ P. Given that,

AB = BC = CD = DE,

BB’= 4 cm and

CC’= 6 cm.

Find AA’ + DD’ + EE’.

48. ABC is a triangle. P is a plane parallel to side BC. Plane P istersect AB at M and AC at N. Given that and BC = 27 cm. Find MN.

4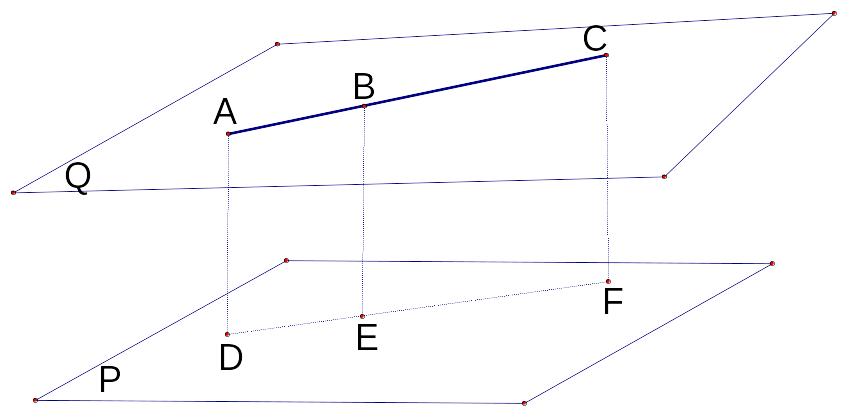 9. In the figure the planes P and Q are parallel to each other. In plane P there are points A, B and C. We draw parallel lines from A, B, C to plane P. They intersect P at the points D, E and F, respectively. Given that, and DF = 44 cm. Find DE.