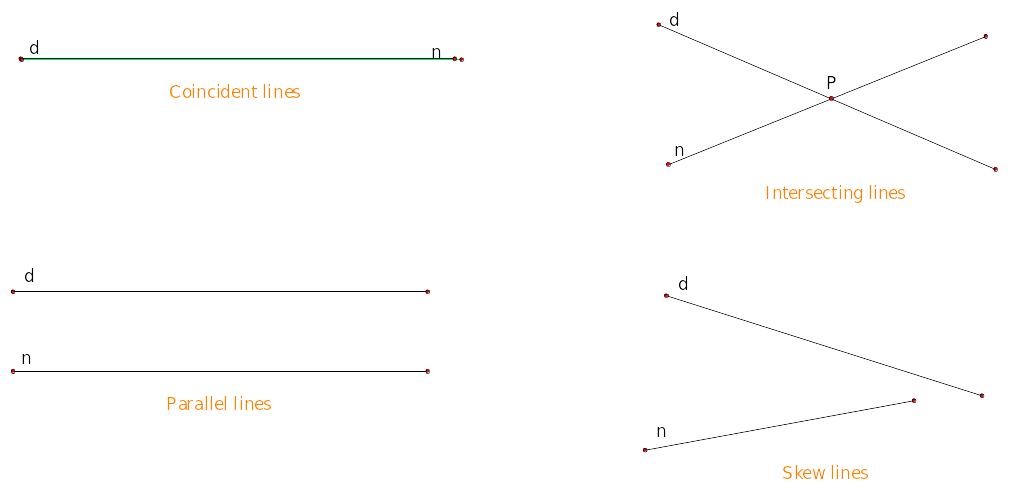
2. Mutual Positions of Two Lines in Space
Two lines in space may have different positions. These are as follows:
Infinitely many intersections: If two lines are coincident then they have infinitely many intersections. Actually, if two lines have two common points, they are coincident.
One common point: From plane geometry we know that if two lines are intersecting and not coincident then they intersect each other at a unique point. We proved that two intersecting lines determine a plane. So intersecting lines are always coplanar lines.
No common point: If two lines have no common points they may have two conditions:
Parallel lines: Parallel lines are defined as coplanar lines having no points in common. From plane geometry we know that, in a plane, through a point not on a line there can be drawn one and only one line parallel to the given line. Similarly we can say that; in space, through a point not on a line, a line parallel to the given line can be drawn and this line is unique.
Skew lines: Two lines are skew to each other if there is not any plane containing both lines. So, these lines can not have any intersection. As it is proven, intersecting lines are always coplanar. By definition skew lines cannot be coplanar. So, skew lines have no common point.
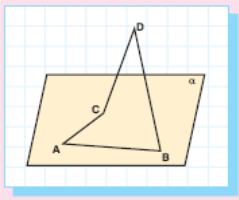
Definition: (Skew Quadrilateral)
A quadrilateral whose vertices are four non-coplanar points is called as a skew quadrilateral.
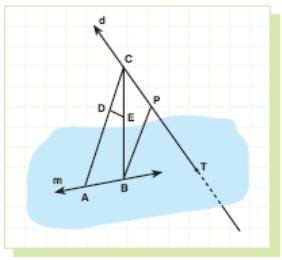
Example 6: In figure, d and m are skew lines. Show that
a) CA and PB are skew lines.
b) DE and d are skew lines.
Solution:
a) If a plane β contains lines CA and PB, this plane contains points C, P, A and B.
Since C and P are two points on d, β contains d and since A and B are two points on m, β contains m.
In this case there will be a plane containing both d and m which is impossible.
Therefore, there is no plane containing CA and PB.
So they are skew lines.
b) Any plane containing DE and d contains points D, E and C.
So this plane contains lines CA and CB because C and D are on CA, and C and E are on CB and by axiom 4 the plane contains CA and CB.
So this plane contains m too by the same axiom.
This is impossible, because m and d are skew lines.
So DE and d are skew lines.
Example 7: ABCD is a skew quadrilateral with side lengths AB = 20 cm and
CD = 16 cm. M and N are the midpoints of the sides BC and AD, E and F are the midpoints of the diagonals BD and AC, respectively. Find the perimeter of the quadrilateral MENF.
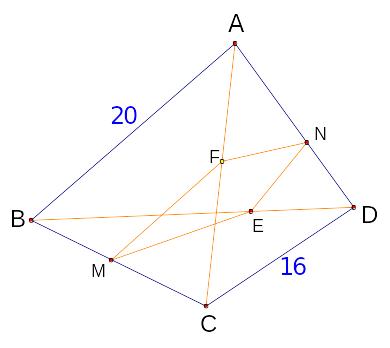
Solution: We know from example 4 that all triangles are coplanar, so ACD, BCD, ABC and ABD are coplanar.
FN // CD and ME // CD then FN // ME,
ME
= FN =
cm.
MF // AB and EN // AB then EN // MF,
EN
= MF =
cm.
As seen MENF is a parallelogram and its perimeter is
P(MENF) = ME + EN + NF + FM = 8 + 10 + 8 + 10 = 36 cm.
Check Yourself 3
1. State the followings as true or false.
a) If lines m and n pass through points M and N, then m and n are coincident.
b) If two lines in space have no common point, they are parallel.
c) Skew lines can be coplanar or non-coplanar lines.
2. Which of the following figures may not be coplanar?
a) triangle b) rhombus c) regular hexagon d) quadrilateral e) circle
3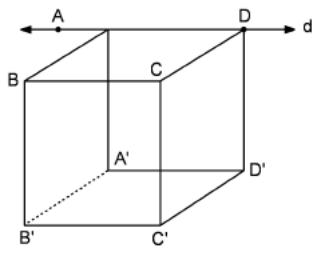
.
In
the figure a cube is given. The line d
passes through side AD. How many skew lines can we draw to the line
d?
4. Which of the following are correct for two lines in space?
a. If they don’t intersect they must be parallel.
b. If they don’t intersect they may be skew lines.
c. If they intersect the intersection is a unique point.
d. If they intersect there may be more than one intersection points.
e. Their intersection is either a point or a line segment.
f. If they are coincident they may have some points which are not common.
5. Three lines are given in space. At which conditions another line cut all of these three lines?
Answers
1. a) True b) False c) False 2. d) quadrilateral 3. 12
4. b and c 5. i. When the three lines are coincident, ii. When these three lines are in the same plane.