1. Introduction to space geometry

A. AXIOMS OF SPACE GEOMETRY

Until this topic we studied on the plane geometry. In that part of the geometry we learned definitions and properties of the figures in the plane. However we live in three dimensional world. Therefore it is necessary to extend our study of geometry to include figures having three dimensions, that is, figures having thickness as well as length and width.

Definition: (Space geometry)

The geometry of three dimensional figures is called three-dimensional geometry or space geometry.

In this chapter we will study lines and planes in space. We will state axioms, definitions and theorems about them. In proofs of theorems sometimes we will use theorems from plane geometry and we will not prove them.

Definition: (Collinear, non-collinear, coplanar, non-coplanar)

The points which are on the same line are called as collinear points and the points which are not on the same line are called as non-collinear points. By the same way the points or lines lying in the same plane are called coplanar points or coplanar lines. If they are not lying in the same plane they are non-coplanar points or non-coplanar lines.

As well as the axioms of plane geometry we have got the axioms of the space geometry. Now, let us state these axioms of space geometry.

Axioms of Space Geometry

1. Two different points in space determine a line.

2. Three non-collinear points in space determine a plane.

3. In space, there are at least two points on a line and there is at least one point outside of this line.

4. A plane having two points in common with a line contains this line.

5. If two planes has a common point then there is a common line passing through this point. (i.e, the intersection of two intersecting planes is a line)

6. In space, outside of a plane there is at least one point.

7. A plane divide a space into two semispaces.

By using these axioms we can get some theorems and corollaries. Also we can prove the theorems and corollaries by using the axioms of space geometry.

Example 1: ABCD is a trapezoid so that AB // CD, E is a point on the line

segment DC, and P is a point not in plane ABC. Q is the intersection point of line AE and plane PBC. If ∠CBA = 90°, AB = 9 cm, EC = 3 cm, and BC = 8 cm, find EQ.

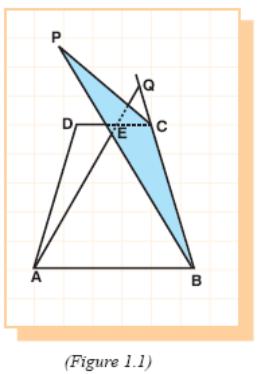
Solution:

Since points A and E are in plane ABCD, all points on line AE are in that plane by axiom 4.

Since the intersection of planes ABC and PCB is line

BC, intersection of line AE and plane PCB is on BC by axiom 5 and axioms of plane geometry.

Since both AE and BC are in plane ABCD,they intersect.

This intersection is given as Q. (Figure 1.1)

From plane geometry we know that EC // AB and so QEC and QAB are similar.

So . So, QC = 4 cm.

∠ECQ = ∠CBA =90° .

Hence, by applying the Pythagorean theorem in ECQ, we get EC² + QC² = EQ²,

3² + 4² = EQ² and EQ = 5 cm.

Example 2: Side BC of ABC lies in a plane α. M and N are two points on sides AB

and AC respectively. Show that if M is not in α then N is not in α either.

S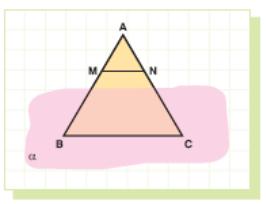 olution:

Assume that N is in α.

Then since C and N are in α, the line AC will be in α by axiom 4.

Since AC is in α then point A is in α too.

Then two points, A and B, on side AB will be in α.

So all points on AB are in α by axiom 4.

However we know that M is not in α. So, N is not in α.

Check Yourself 1

1. State the followings as true or false

a) Three points determine a plane

b) If the endpoints of a line segment are in a plane its midsegment is in the same plane

c) There can be drawn two planes whose intersection is a unique point

2. There are n non-coplanar points (n ≥ 4). Show that n – 1 of them can not be collinear.

3. Draw the following statements.

a. The points A and B are lying in the plane X.

b. The line d lie in plane X but line m does not lie in X.

c. The line d lie in plane X, points A and B also lie in X. A is on the line d but B is not on the line d.

4. At least how many parts can 4 different lines divide a plane?

5. Two points of plane P is common with two points of plane Q. What can we say about these two points?

Answers

1. a) F b) T c) F

2. Hint: If the points are collinear then they are also coplanar.

3 .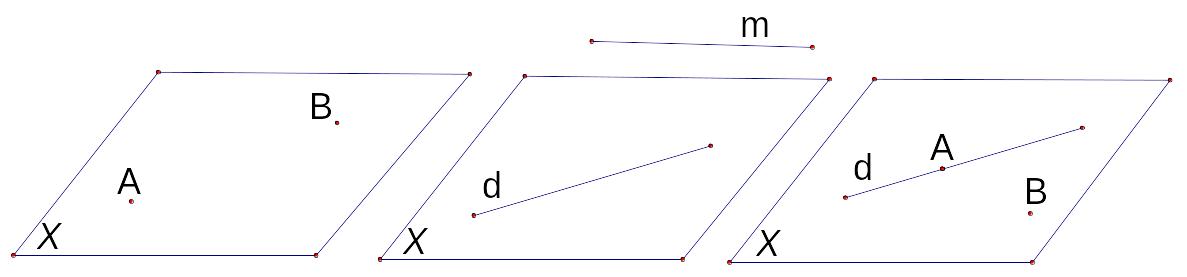

4. 5

5. The points are on the intersection line of given planes.

B. LINES AND PLANES IN SPACE