МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”

Комп’ютерна графіка

Методичні вказівки

до виконання лабораторної роботи № 8

Растрова розгортка багатокутників

для студентів бакалаврського рівня підготовки спеціальності

«Комп‘ютерні науки» та «Видавничо-поліграфічна справа»

Затверджено на засіданні кафедри

Інформаційні технології видавничої справи

Протокол № 5-11/12 від 23 грудня 2011 р.

Львів – 2012

Растрова розгортка багатокутників: Методичні вказівки до лабораторної роботи № 8 з курсу “Комп’ютерна графіка” для студентів «Видавничо-поліграфічна справа» (шифр - 0927) та “Комп‘ютерні науки” (шифр - 0804) / Укл.: О.Я. Різник - Львів: Видавництво Національного університету “Львівська політехніка”, 2012 - 15 с.

Укладач: Різник О.Я., к.т.н., доц.

Відповідальний за випуск: Різник О. Я., к. т. н., доц.

Рецензент: Рашкевич Ю.М., д.т.н., проф.

Лабораторна робота № 8 Растрова розгортка багатокутників

Мета роботи: Освоїти алгоритми растрової розгортки

ТЕОРЕТИЧНІ ВІДОМОСТІ

8.1 Метод ScanLine

Для растрових графічних пристроїв сусідні піксели на скануючому рядку, ймовірно, мають однакові характеристики. Це когерентність растрових рядків.

Характеристики пікселів на даному рядку змінюються тільки там, де ребро багатокутника перетинає рядок. Ці перетини поділяють скануючий рядок на області.

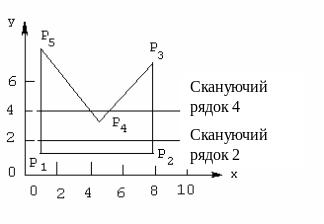
Рис.8.1. Растрова розгортка суцільної області

Для простого багатокутника на рис.8.1 рядок 2 перетинає багатокутник при х=1 і х=8. Одержуємо три області:

x<1 поза багатокутником

1x8 всередині багатокутника

x>8 поза багатокутником

Рядок 4 поділяється на п’ять областей:

x<1 поза багатокутником

1x4 всередині багатокутника

4<x<6 поза багатокутником

6x8 всередині багатокутника

x>8 поза багатокутником

Зовсім необов’язково, щоб точки перетинану для рядка 4 відразу визначалися у фіксованому порядку (ліворуч праворуч). Наприклад, якщо багатокутник задається списком вершин P₁P₂P₃P₄P₅, а список ребер - послідовними парами вершин Р₁Р₂, Р₂Р₃, Р₃Р₄, P₄P₅, P₅P₁ то для рядка 4 будуть знайдені наступні точки перетину з ребрами багатокутника: 8, 6, 4, 1. Ці точки треба відсортувати в зростаючому порядку по х, тобто одержати 1, 4, 6, 8.

При визначенні інтенсивності, кольору і відтінку пікселів на скануючому рядку розглядаються пари відсортованих точок перетинань. Для кожного інтервалу, що задається парою перетинань, використовується інтенсивність чи колір заповнюваного багатокутника. Для інтервалів між парами перетинань і крайніх (від початку рядка до першої точки перетину і від останньої точки перетину до кінця рядка) використовується фонова інтенсивність чи колір. На рис.8.1 для рядка 4 у фоновий колір встановлені піксели: від 0 до 1, від 4 до 6, від 8 до 10, тоді як піксели від 1 до 4 і від 5 до 8 зафарбовані в колір багатокутника.

Точне визначення тих пікселів, що повинні активуватися вимагає деякої обережності. Розглянемо простий прямокутник, зображений на рис.8.2. Прямокутник має координати (1,1) (5,1), (5,4), (1,4). Скануючі рядки з 1 по 4 мають перетини з ребрами багатокутника при х=1 і 5. Згадаємо, що піксел адресується координатами свого лівого нижнього кута, виходить, для кожного з цих скануючих рядків будуть активовані піксели з x-координатами 1, 2, 3, 4 і 5. На рис.8.2(а) показаний результат. Помітимо, що площа, що покривається активованими пікселами, дорівнює 20, у той час як дійсна площа прямокутника дорівнює 12.

а б

Рис. 8.2. Система координат рядків сканування

Модифікація системи координат скануючого рядка і тесту активації усуває цю проблему, як це показано на рис.8.2(б). Вважається, що скануючі рядки проходять через центри рядків пікселів, тобто через середини інтервалів, як це показано на рис.8.2(б). Тест активації модифікується в такий спосіб: перевіряється, чи лежить всередині інтервалу центр піксела, розташованого праворуч від перетину. Однак піксели все ще адресуються координатами лівого нижнього кута. Як показано на рис.8.2(б), результат даного методу коректний.

Горизонтальні ребра не можуть перетинати скануючий рядок і, таким чином, ігноруються. Це зовсім не означає, що їх немає на малюнку. Ці ребра формуються верхнім і нижнім рядками пікселів, як показано на рис.8.2. Рис.8.2 ілюструє коректність верхнього і нижнього ребер багатокутника, отриманих у результаті модифікації системи координат скануючих рядків.

Додаткові труднощі виникають при перетині скануючого рядка і багатокутника точно по вершині, як це показано на рис.8.3.

Рис.8.3. Особливості перетинів з рядками сканування

При використанні угоди про середину інтервалу між скануючими рядками одержуємо, що рядок у=3,5 перетне багатокутник у 2, 2 і 8, тобто вийде непарна кількість перетинань. Отже, розбивка пікселів на пари - дасть невірний результат, тобто піксели (0, 3), (1, 3) і від (3, 3) до (7, 3) будуть фоновими, а піксели (2, 3), (8, 3), (9, 3) зафарбуються в колір багатокутника. Тут виникає ідея враховувати тільки одну точку перетинання з вершиною. Тоді для рядка у=3,5 одержимо правильний результат. Однак результат застосування методу до рядка у=1,5, що має два перетини в (5, 1), показує, що метод невірний. Для цього рядка саме розбивка на пари дасть вірний результат, тобто пофарбований буде тільки піксел (5, 1), Якщо ж враховувати у вершині тільки одне перетинання, то піксели від (0, 1) до (4, 1) будуть фоновими, а піксели від (5, 1) до (9, 1) будуть зафарбовані в колір багатокутника.

Правильний результат можна одержати, враховуючи точку перетинання у вершині два рази, якщо вона є точкою локального мінімуму чи максимуму і враховуючи її один раз в іншому випадку. Визначити локальний максимум чи мінімум багатокутника в розглянутій вершині можна за допомогою перевірки кінцевих точок двох ребер, з’єднаних у вершині. Якщо в обох кінців координати у більші, ніж у вершини, виходить, вершина є точкою локального мінімуму. Якщо менші, значить, вершина - точка локального максимуму. Якщо одна більша, а інша менша, то вершина не є ні точкою локального мінімуму, ні точкою локального максимуму. На рис.8.3 точка P₁ - локальний мінімум, Р₃ - локальний максимум, а Р₂, Р₄ - ні то і ні інше. Отже, у точках Р₁ і P₃ враховуються два перетинання із скануючими рядками, а в Р₂ і Р₄ - одне.