Линейные модели

Главная причина популярности нейронных сетей кроется в их способно­сти моделировать нелинейные задачи, т.е. задачи классификации, которые нельзя решить, проводя гиперплоскость между классами, и задачи регрес­сии, которые нельзя решить, проводя гиперплоскость через данные.

При этом, однако, не следует пренебрегать и простыми линейными моде­лями. Часто оказывается, что задача, считавшаяся сложной и нелинейной, на самом деле может быть успешно решена линейными методами, и, во всяком случае, линейная модель является хорошей точкой отсчета для сравнения эффективности различных более сложных методов.

В пакете ST Neural Networks линейные модели строятся с помощью спе­циального типа нейронных сетей - линейных. Линейная сеть имеет всего два слоя: входной и выходной слой, имеющий линейные PSP-функции и функции активации. Как и выходной слой RBF-сети, линейная сеть опти­мизируется непосредственно с помощью метода псевдообратных.

Чтобы построить линейную модель в задаче регрессии для ирисов, вос­пользуемся диалоговым окном Создать сеть - Create Network: выберем тип сети Линейная - Linear. Советник - Network Advisor автоматически сконфигурирует все остальные параметры сети.

После того, как сеть построена, обучим ее, нажав кнопку Псевдообрат­ные - Pseudo-Inverse в диалоговом окне Радиальная базисная функция -Radial Basis Function (на самом деле эта кнопка оптимизирует выходной слой любой сети в предположении, что PSP-функции и функции актива­ции этого слоя линейны).

Посмотрев статистики регрессии (мы предполагаем, что используется тот же самый набор данных), вы обнаружите, что Отношение ст. откл. при обучении - Trainings.D. Ratio равно 0,1135, а Контрольное отношение ст. откл. - Verification S.D. Ratio равно 0,1723. Результат действительно полу­чился того же порядка, что у нелинейных моделей, хотя вполне вероятно, что мы не выжали из нелинейных моделей все, на что они способны.

Сети Кохонена

Обсуждение

В сетях Кохонена происходит неуправляемое обучение (без учителя): сеть учится распознавать кластеры среди неразмеченных обучающих данных, содержащих только входные значения.

Кроме этого, сеть Кохонена располагает родственные кластеры поблизо­сти друг от друга в выходном слое, формируя так называемую топологи­ческую карту (Topological Map) (Haykin, 1994; Fausett, 1994; Patterson, 1996).

Сети Кохонена используются не так, как сети других типов, и пакет ST Neural Networks имеет специальные средства для работы с ними, в том числе:

1. Окно Частоты выигрышей - Win Frequencies, в котором показывает­ся, где в сети формируются кластеры.

2. Окно Топологическая карта - Topological Map, которое показывает, какие наблюдения отнесены к тому или иному кластеру, и помогает пользователю правильно пометить элементы и наблюдения.

Для упражнения мы возьмем видоизмененный вариант файла Iris.sta с четырьмя входными и одной выходной переменной (как в исходном фай­ле) и 30-ю обучающими и 30-ю контрольными наблюдениями. Обратите внимание на то, что хотя сеть Кохонена при обучении не нуждается в вы­ходных значениях, она будет их использовать, если такие значения име­ются в файле. Выход сети Кохонена в пакете ST Neural Networks всегда будет номинальной переменной (т.е. такая сеть всегда выполняет класси­фикацию).

Построим сеть Кохонена с помощью диалогового окна Создать сеть -Create Network, задав в нем тип Сети Кохонена - Kohonen. Советник -Network Advisor автоматически определит большинство параметров пре/пост-процессирования, включая (в данном случае) номинальную вы­ходную переменную с тремя классами-значениями (Setosa, Versicol и Virginic).

Сеть Кохонена всегда состоит из двух слоев: входного слоя и выходного - топологической карты. Выходной слой сети Кохонена отличается тем, что он располагается в двумерном пространстве. Чтобы задать слой, нужно указать общее число элементов в столбце Элементы - Units и ширину слоя в столбце Ширина - Width (чтобы увидеть этот столбец, прокрутите таблицу в горизонтальном направлении). Программа ST Neural Networks определит высоту слоя, поделив число элементов на ширину.

В этом примере нам будет достаточно топологической карты 4x4. Таким образом, нужно задать число элементов выходного слоя равным шестна­дцати, а его ширину - четырем.

Замечание. Ширину можно задавать для любого слоя любой сети пакета ST Neural Networks. Однако только в случае сети Кохонена этот параметр будет иметь принципиальное значение. Во всех остальных случаях един­ственным следствием выбора ширины будет тот или иной внешний вид сети в окне Рисунок сети - Network Illustration.

Обучение сети Кохонена

Алгоритм обучения сети Кохонена корректирует положение центров в слое топологической карты таким образом, чтобы приблизить их к цен­трам кластеров в обучающих данных. На каждом шаге обучения алгоритм выбирает элемент, чей центр лежит ближе всего к обучающему наблюде­нию. Этот элемент и соседние с ним затем корректируются так, чтобы они больше походили на данное обучающее наблюдение.

Исключительно важную роль в обучении Кохонена играет окрестность элемента. Корректируя не только сам выигравший элемент, но и соседние с ним, алгоритм Кохонена относит близкие наборы данных к смежным областям топологической карты. По ходу обучения окрестность посте­пенно сужается, и одновременно уменьшается скорость обучения, так что поначалу выстраивается грубое отображение (при котором на одно на­блюдение откликаются большие группы элементов), а на последующих этапах достраиваются более тонкие детали (так что отдельные элементы в группах реагируют на небольшие различия в данных).

Замечание. Как и в случае метода обратного распространения, в окне График обучения - Training Graph выводится среднеквадратичная ошибка. Однако в данном случае смысл этой ошибки совершенно иной, чем для обратного распространения.

В методе обратного распространения берется сумма квадратов значений функции ошибок, которая измеряет расстояние от выходного вектора сети до целевого выходного вектора. При этом ошибка, которая выдается в окне График обучения - Training Graph - это среднеквадратичное значе­ние ошибки выхода, взятое по всему обучающему множеству.

В обучении методом Кохонена функция ошибок - это расстояние от век­тора весов выигравшего радиального элемента до входного вектора. Та ошибка, которая выдается в окне График обучения - Training Graph - это среднеквадра­тичное значение этой входной ошибки, взятое по всему обучающему множеству.

Диалоговое окно Обучение сети Кохонена -Kohonen Training, которое открывается командой Кохонен - Kohonen... меню Обучить - Train или кнопкой , содержит начальные и конечные значения параметров Скорость обучения - Learning rate и Окре­стность - Neighborhood. Часто обучение Кохонена явным образом разде­ляется на фазу грубого приближения (упорядочивания) и фазу уточнения.

В нашем случае достаточная эффективность достигается при двух этапах по пятьдесят эпох в каждом. На первом этапе зададим уменьшение пара­метра Скорость обучения - Learning rate с начального значения 0,5 до конечного значения 0,1, а размер окрестности будем все время сохранять равным единице. На втором этапе скорость обучения будем держать по­стоянной и равной 0,1, а размер окрестности равным нулю.

После того, как сеть Кохонена обучена, можно рассмотреть ее, чтобы уз­нать, какие кластеры она образовала и чему они соответствуют.

В нашем примере мы будем делать это с известным лукавством, посколь­ку мы заранее знаем всю структуру данных (для применения сетей Кохо­нена это нетипично).

Частоты выигрышей

В диалоговом окне Частоты выигрышей - Win Frequencies, которое от­крывается одноименной командой меню Статистики - Statistics, можно наблюдать за тем, где на топологической карте формируются кластеры. Это окно прогоняет сеть по всем наблюдениям из обучающего множества и подсчитывает, сколько раз каждый элемент выигрывал (т.е. оказывался ближайшим к обрабатываемому наблюдению).

Большие значения частоты выигрышей указывают на центры кластеров в топологической карте.

Элементы с нулевой частотой выигрышей вообще не были использованы, и часто это считается признаком того, что обучение не было особенно успешным (так как сеть не использовала все свои ресурсы). Однако, в на­шей задаче так мало обучающих наблюдений, что некоторые из элементов неизбежно окажутся незадействованными.

В окне Частоты выигрышей - Win Frequencies статистики выдаются раз­дельно для обучающего и контрольного множеств (контрольные стати­стики выводятся красным цветом ниже темной горизонтальной черты). Если показатели кластеризации для этих двух множеств существенно раз­личаются, это свидетельствует о том, что сеть не научилась хорошо обобщать. В нашем примере обучающее множество настолько мало, что можно не обращать внимания на такие несоответствия.

Окно топологической карты

После того, как зафиксировано распределение центров кластеров, средст­вами окна Топологическая карта - Topological Map можно протестировать сеть с целью выяснить смысл кластеров.

В окне Топологическая карта- Topological Map (которое открывается кнопкой ) выходной слой представлен графически в пространстве двух измерений. При обработке очередного наблюдения каждый элемент пока­зывает степень своей близости к нему с помощью сплошного черного квадратика (чем больше размер квадрата, там больше степень близости), а выигравший элемент помещается в квадратную рамку.

При тестировании сети на нескольких наблюдениях (удобнее всего делать это с помощью верхней стрелки кнопок микропрокрутки, расположенной рядом с полем Номер наблюдения - Case No) по структуре активаций вы увидите, как группируются похожие элементы и как они реагируют на близкие наблюдения.

Теперь мы можем начать помечать элементы, устанавливая этим смысл соответствующих им кластеров. В нашем примере первые десять наблю­дений соответствуют виду Setosa.

Запустите (командой Rim) первое наблюдение, затем пометьте выиграв­ший элемент следующим образом. Поместите указатель мыши на картин­ку топологической карты и нажмите правую кнопку мыши - откроется контекстное меню Топологические классы - Topological Classes. Выберите из него нужный класс (Setosa). Вы увидите, что имя выигравшего элемен­та топологической карты изменилось.

Пропустите через сеть остальные обучающие наблюдения, соответствен­но помечая выигравшие элементы. Здесь вы можете столкнуться с таким неудобством: элементы можно помечать только с помощью обучающих наблюдений, а последние разбросаны по всему набору данных. Проще всего поступить так: в меню Правка-Переменные- Edit-Variables выбери­те функцию Перемешать - Shuffle и команду Сгруппировать множества - Croup Sets. Программа ST Neural Networks соберет все наблюдения из обучающего множества и поместит их в начало набора данных.

Может получиться так, что некоторый элемент будет выигрывать на на­блюдениях как класса Versicolor. так и класса Virginiccr, пометьте его зна­ком вопроса (неясный). Просмотрев все тестовые наблюдения, оставшие­ся незанятыми элементы можно также пометить как неиспользуемые (?). Или же можно еще раз пропустить все наблюдения и посмотреть, на ка­кой класс сильнее реагирует данный неиспользуемый элемент, и соответ­ствующим образом его пометить.

После того, как всем элементам приписаны метки, в окне Топологическая карта - Topological Map можно посмотреть, насколько хорошо сеть Кохонена классифицирует контрольное множество.

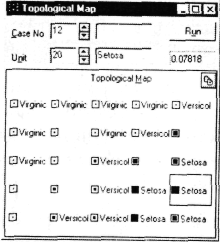
Когда сеть Кохонена применяется для решения реальной задачи, то, как правило, заранее бывает неизвестно, какие кластеры встретятся в данных. В таком случае следует пометить кластеры символами (идентифицируя их с помощью таблицы Частоты выигрышей - Win Frequencies), а затем исследовать данные, чтобы попытаться определить, какой смысл могут иметь выявленные кластеры.

Чтобы облегчить эту работу, программа ST

Neural Networks позволяет помечать наблюдения в окне Топологическая карта - Topological Map. Для этого нужно придерживаться описанной далее последовательности действий (не делайте этого сейчас - в этом нет нужды, так как данные про ирисы уже помечены).

1. Обучить сеть Кохонена.

2. Средствами окна Частоты выигрышей - Win Frequencies идентифи­цировать кластеры в окне Топологическая карта - Topological Map.

3. Пометить кластеры символическими именами (например, С1, С2 и т.д.). Чтобы присвоить кластеру новое имя, выберите элемент в окне Топологическая карта - Topological Map и затем пункт Создать -New... в контекстном меню. Таким образом можно редактировать вы­ходную переменную сети, добавляя ей новые номинальные значения(соответствующие именам кластеров).

4. Протестировать наблюдения в окне Топологическая карта - Topological Map и присвоить наблюдениям имена кластеров.

5. Исследовать данные (возможно, обратившись к исходной прикладной задаче) с целью определить, что представляют собой выявленные кластеры.

6. Заменить символические имена кластеров смысловыми.

7. Вновь протестировать наблюдения и пометить их согласно выиграв­шим элементам.