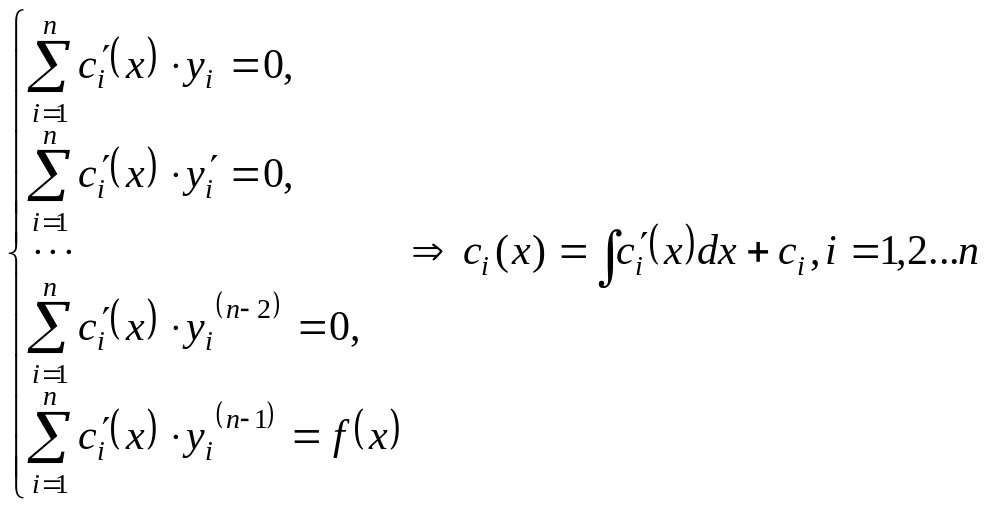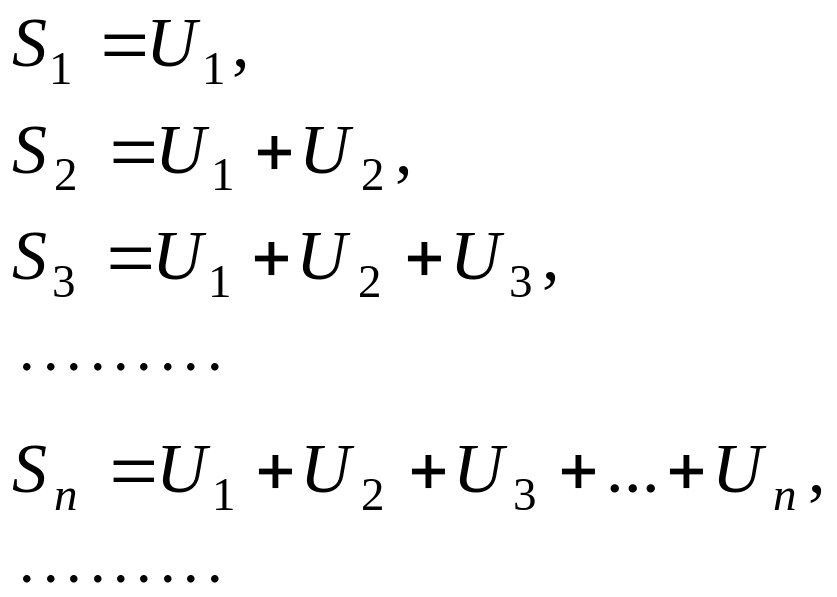- •Учебные карты. Часть 2
- •Введение
- •1. Таблица производных
- •2. Таблица интегралов
- •3. Методы интегрирования
- •4. Некоторые интегралы, содержащие квадратный трехчлен.
- •5. Интегралы от некоторых рациональных функций
- •6. Интегралы, содержащие тригонометрические и показательные функции
- •7. Несобственные интегралы
- •8. Функции нескольких переменных
- •10. Задачи о массе фигуры
- •11.Криволинейный интеграл по длине дуги
- •12. Системы координат
- •13. Двойной интеграл
- •14. Тройной интеграл
- •15. Приложения интегралов по фигуре в геометрии
- •16. Приложение интегралов по фигуре в механике
- •17. Скалярное поле (стационарное)
- •18. Векторное поле. Характеристики векторного поля
- •19. Дифференциальные уравнения первого порядка
- •20. Виды дифференциальных уравнений высших порядков, допускающих понижение порядка
- •21. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами
- •22. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами
- •23. Числовые ряды. Основные понятия
- •24. Числовые ряды с положительными членами
- •25. Знакопеременные числовые ряды
- •26. Функциональные ряды. Основные понятия
- •27. Степенные ряды
- •28. Разложение функции в степенной ряд
- •29 .Таблица разложений некоторых функций в степенные ряды
- •30. Разложение функции в тригонометрический ряд Фурье
22. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами
Вид уравнения:
|
Метод вариации произвольных постоянных |
Метод подбора частного решения |
Если
если
где
Частный случай:
где
где
|
Частное
решение
То
есть
|
|
Структура общего решения:
где
|
||
Если
то
|
23. Числовые ряды. Основные понятия
№ п/п |
Понятие |
Определение и обозначение |
||
1. |
Ряд |
|
||
2. |
Члены ряда, общий ( n – ый ) член ряда |
|
||
3. |
Частичные суммы ряда |
|
||
4. |
Последовательность частичных сумм |
|
||
5. |
Сходящиеся ряды |
|
||
6. |
Расходящиеся ряды |
|
||
7. |
Остаток ряда |
|
||
Основные свойства сходящихся рядов |
||||
|
|
|
||
|
|
|
||
сходится, – его сумма |
|
|
||
сходится,
|
|
|||
Необходимый признак сходимости ряда |
||||
- сходится |
|
|
||
Замечание:
|
|
- расходится |
||
24. Числовые ряды с положительными членами
Определение
|
||||||||
Некоторые ряды и их поведение |
1 |
Гармонический
ряд
|
||||||
2 |
Обобщенный
гармонический ряд
|
|||||||
3 |
Ряд геометрический |
|
||||||
В
частности при
|
|
|||||||
Достаточные признаки сходимости числовых рядов с положительными членами |
||||||||
Признаки сравнения |
Интегральный признак Коши |
Признак Даламбера |
Признак Коши |
|||||
|
,
Замечание:
|
|
|
|||||
1.
где
(при
|
|
и
одновременно сходятся или расходятся |
а)
б)
|
а) - сход. б) - расход. |
||||
2. а)
|
|
сход |
Замечание: 1.
Если
2. Признак Даламбера иногда используется без предельного перехода:
|
|||||
б)
|
|
расход. |
||||||
Замечание:
В качестве рядов для сравнения удобно
выбирать ряды
|
||||||||