
- •Учебные карты. Часть 2
- •Введение
- •1. Таблица производных
- •2. Таблица интегралов
- •3. Методы интегрирования
- •4. Некоторые интегралы, содержащие квадратный трехчлен.
- •5. Интегралы от некоторых рациональных функций
- •6. Интегралы, содержащие тригонометрические и показательные функции
- •7. Несобственные интегралы
- •8. Функции нескольких переменных
- •10. Задачи о массе фигуры
- •11.Криволинейный интеграл по длине дуги
- •12. Системы координат
- •13. Двойной интеграл
- •14. Тройной интеграл
- •15. Приложения интегралов по фигуре в геометрии
- •16. Приложение интегралов по фигуре в механике
- •17. Скалярное поле (стационарное)
- •18. Векторное поле. Характеристики векторного поля
- •19. Дифференциальные уравнения первого порядка
- •20. Виды дифференциальных уравнений высших порядков, допускающих понижение порядка
- •21. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами
- •22. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами
- •23. Числовые ряды. Основные понятия
- •24. Числовые ряды с положительными членами
- •25. Знакопеременные числовые ряды
- •26. Функциональные ряды. Основные понятия
- •27. Степенные ряды
- •28. Разложение функции в степенной ряд
- •29 .Таблица разложений некоторых функций в степенные ряды
- •30. Разложение функции в тригонометрический ряд Фурье
4. Некоторые интегралы, содержащие квадратный трехчлен.
Обозначение:
![]() ,
,
![]()
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
|
5. Интегралы от некоторых рациональных функций
Обозначение:
![]() .
.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
|
6. Интегралы, содержащие тригонометрические и показательные функции
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
|
7. Несобственные интегралы
|
Условие |
Определение и обозначение |
Геометрическая иллюстрация сходящихся интегралов |
1. Интегралы с бесконечными пределами интегрирования |
где
|
|
|
- непрерывна на , где
|
|
|
|
- непрерывна на
где
|
интеграл
сходится, если сходятся оба интеграла
|
|
|
2. Интегралы от неограниченных функций |
|
|
|
|
|
|
|
|
интеграл сходится, если сходятся оба интеграла сходятся |
|
|
|
Замечание 1. Если при отыскании предела окажется, что он не существует, то несобственный интеграл типа 1 и 2 называется расходящихся |
||
3. Теоремы сравнения |
|
||
|
|||
- расходится,
|
|||
Замечание 2. Теоремы сравнения имеют место и для всех интегралов типа 1 и 2 |
|||
8. Функции нескольких переменных
Определение функции |
Графическое изображение |
Множество равных уровней |
Предел функции |
Непрерывность |
|||
(функция
В частности,
1.
2.
|
|
|
1.
2.
выполняется
Замечание.
Предел функции не зависит от способа
стремления т.
|
Функция
1. определена в точке и некоторой ее окрестности ;
2.
3.
где
|
|||
Частные производные |
Дифференциал |
||||||
Определение |
Геометрическое изображение |
Определение |
Применение дифференциала к приближенным вычислениям |
||||
В частности, ,
Замечание.
Частная производная по переменной
|
|
-
дифференцируемая функция в т.
где
|
В
частности,
где
|
||||
9. Дифференциальное исчисление функций нескольких переменных (n=2)
Сложные функции и их дифференцирование |
Неявно заданные функции и их дифференцирование |
|||
1
2
3
.
|
Уравнение
|
|||
Приложения дифференциального исчисления |
||||
Экстремум функции 2-х переменных |
Касательная плоскость и нормаль к поверхности |
|||
Определение |
Необходимые условия существования экстремума |
Достаточные условия существования экстремума |
1) - уравнение поверхности
уравнение касательной плоскости
2)
уравнение нормали к поверхности |
|
|
Замечание. Экстремум возможен и в тех точках, где хотя бы одна из частных производных не существует |
1.
а)
т.
б)
т.
2.
3.
|
||










 ,
,


 .
.

 .
.
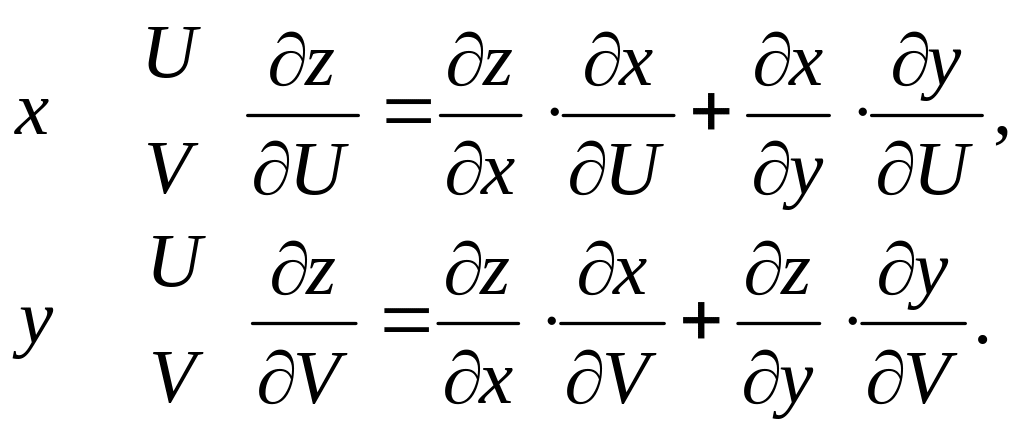
 -
-
