Лабораторная работа №8 Решение задач на определение качества скважинных измерений.

Цель работы: Освоение теории статистических методов оценки качества скважинных измерений.

Оснащение занятий: тетрадь, карандаши, калькулятор, ручка.

План выполнения работы:

1. Изучить теоретические основы.

2. Выполнить задания к лабораторной работе.

3. Подвести итоги.

План оформления отчета:

По результатам выполненной работы составить отчет, в котором приводятся:

1. тема работы;

2. цель работы;

3. план выполнения работы;

4. краткий конспект теоретических основ лабораторной работы;

5. необходимые расчеты;

6. подведенные итоги.

Теоретические основы.

Теоретическим обоснованием новой технологии стандартизации геофизических СИ в разрезах контрольных скважин явилась теорема Чебышева, известная под названием закон больших чисел.

Практическая значимость этой теоремы Чебышева заключается в том, что при усреднении достаточно большого числа независимых и одинаково распределенных случайных величин можно получить с вероятностью, как угодно близкой к единице, значение измеряемой величины, сколь угодно мало отличающееся от ее математического ожидания.

При этом арифметическое достаточно большого числа случайных величин, имеющих ограниченные дисперсии, утрачивает характер случай­ной величины. Объясняется это тем, что отклонения каждой из величин от их математических ожиданий могут быть как положи­тельными, так и отрицательными, а в среднем арифметическом случайных величин эти отклонения взаимно погашаются.

Для того чтобы к измерениям физических величин можно было применить теорему Чебышева, требуется выполнение сле­дующих условий:

1. случайные величины должны быть по­парно независимыми;

2. они должны иметь одно и то же матема­тическое ожидание;

3. дисперсии этих величин должны быть ограничены одним и тем же числом.

При проведении геофизических измерений в скважинах выпол­няются все эти требования. Действительно, результат каждого последующего повторного измерения в скважине не зависит от предыдущего замера. Второе требование выполняется, если среднее геофизические измерения произведены без систематических оши­бок, имеющих односторонний характер или, что одно и то же, один знак. Наконец, последнее требование обеспечивается нор­мированием метрологических характеристик геофизических СИ, гарантирующим ограничение дисперсий измеряемых величин одним и тем же числом.

Основываясь на законе больших чисел, можно утверждать, что по серии повторных замеров в контрольных скважинах мож­но определить действительные значения параметров геологи­ческого разреза в характерных точках - опорных пластах или экстремальных точках, - как угодно близкие к их истинным значениям. Другими словами, в этих сооружениях можно полу­чить, при соблюдении ряда специальных требований по контролю неизменности пластовых условий, ряд эталонных значений физи­ческих параметров, по которым можно оценивать метрологи­ческие характеристики геофизических ИИС.

Опыт работы показал, что наиболее полно принцип стандар­тизации геофизических СИ на основе повторных замеров реали­зуется в специально обустроенных контрольных (контрольно-поверочных) скважинах, в которых можно выделить или вос­создать необходимое количество опорных пластов. Аттестация разреза такой скважины по специальной программе позволяет составить каталог действительных значений параметров опорных пластов, так называемую «образцовую» кривую, и по серии пов­торных замеров оценить качество измерений контролируемых комплектов геофизической аппаратуры.

ГОСТ 16.263-70 определяет два важнейших показателя ка­чества измерений - сходимость и воспроизводимость. При изме­рениях в контрольных скважинах абсолютная погрешность сходи­мости измерений характеризуется величиной расхождения между первым х₁ и вторым х₂ замерами параметра:

(8.1)

Относительная погрешность сходимости замеров определяется отношением абсолютной погрешности Δх_С к среднему значению параметра по двум измерениям:

(8.2)

Воспроизводимость измерений оценивается близостью показа­ний контролируемого комплекта аппаратуры к действительным значениям физических параметров в опорных пластах контроль­ной скважины.

Оценка воспроизводимости i замера в какой-либо точке отсчета с помощью абсолютных Δх_В ошибок замеров регистрируемо­го параметра производится по разности:

(8.3)

где хij - значение параметра х в точке i снятия отсчета; xicp - среднее значение параметра х в этой же точке образцо­вой кривой, определяемое как среднеарифметическое значение параметра х из серии т повторных замеров.

Относительная ошибка δx_В воспроизводимости j замера в точке i определяется как отношение абсолютной ошибки δx_В параметра х к значению параметра x_icp в этой же точке:

(8.4)

При проведении исследовательских работ в качестве вспомо­гательного показателя качества измерений может использовать­ся показатель воспроизводимости θ_В, показывающий, во сколько раз разброс повторных замеров в пласте меньше дифференциации этого параметра в разрезе скважины. Этот показатель опре­деляется отношением среднеквадратичного отклонения воспроиз­водимости S_B параметра в пласте к среднеквадратичному откло­нению дифференциации (изменчивости) S_Д этого параметра в разрезе скважины (в %):

(8.5)

Важнейшим достоинством технологии стандартизации геофизи­ческих СИ в контрольных скважинах является возможность выде­ления в инструментальных погрешностях систематических и слу­чайных составляющих.

В общем случае полученное в результате измерения значение уi, связано с истинной величиной измеряемого параметра у* соотношением

(8.6)

где А и В - коэффициенты, зависящие от величины система­тической составляющей погрешности; σ_С- случайная погреш­ность.

Физический смысл последнего соотношения виден из рис. 8.1. При отсутствии погрешности измерений все точки зависимости располагаются на прямой у, - у* или (при наличии только случайных погрешностей) вблизи этой прямой. Система­тические погрешности измерений приводят линию регрессии (8.6) к виду

(8.7)

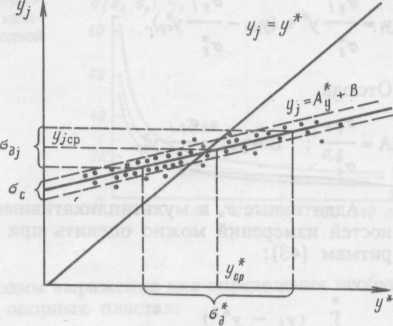
Рисунок 8.1 - Регрессия измеряемых уi и истинных у* физических величин при влиянии инструментальных погрешностей.

Совокупная, или полная, погрешность измерения σ_П будет иметь как случайную σ_С, так и систематическую σ_СТ состав­ляющие:

Величина случайной составляющей будет определяться дис­персией отдельных замеров относительно линии регрессии . Систематическая погрешность, включающая адди­тивную σ_А, и мультипликативную σ_М составляющие, будет опреде­ляться среднеквадратичным отклонением прямой (8.7) от линии регрессии уi= у*.

Аддитивные σ_А, и мультипликативные σ_М составляющие погреш­ностей измерений можно оценить при этом по следующим алго­ритмам:

(8.8)

(8.9)

Принципиальное значение для реализации технологии стан­дартизации геофизических СИ на основе повторных замеров в контрольных скважинах имеет обоснование необходимого коли­чества повторных замеров и числа опорных пластов, в которых должны сниматься отсчеты. Здесь также воспользуемся приемами математической статистики.

В теории ошибок установлены следующие алгоритмы для опре­деления погрешностей статистических оценок:

, (8.10)

где Δуср и Δσу погрешности определения среднего значения параметра у и его среднего квадратического отклонения σу; n- объем выборки; σ_Г- дисперсия генеральной сово­купности; t-гарантийный коэффициент, определяемый за­даваемой вероятностью Ф(t) оценок погрешностей (при Ф = 90% t =1,65).

Из этой формулы находим выражение для определения необхо­димого числа отсчетов в опорных пластах:

(8.11)

Последнее выражение позволяет оценивать объем необходимой выборки повторных замеров при различных вероятностях Ф(t). При вероятности Ф = 90%, гарантийном коэффициенте t=1,65 и допустимой погрешности статистических оценок 10% необходимый объем выборки для достоверной оценки Δуср со­ставит

Ясно, что снятие такого числа отсчетов при ручной ра­боте затруднено, поэтому для решения практических задач необходимо прибегать либо к снижению вероятностей опре­деления статистик Δуср, либо к снижению точности их оценок. Легко показать, что при снижении требований к точности расчета показателей Δуср в два раза, необходимый объем выборки может быть сокращен до 35 отсчетов. Фак­тические данные показывают (рис. 8.2), что в практической работе объем выборки в 10-15 опорных пластах достаточен для расчета показателей Δуср с 10%-ной погрешностью (в опе­ративной работе достаточно иметь до 7-10 опорных пластов).

Определим теперь, какое минимальное число повторных за­меров необходимо для достоверной оценки показателей качества измерений. Число таких замеров можно определить из выражения для ошибки каждого индивидуального измерения уij, выполнен­ного без систематических ошибок,

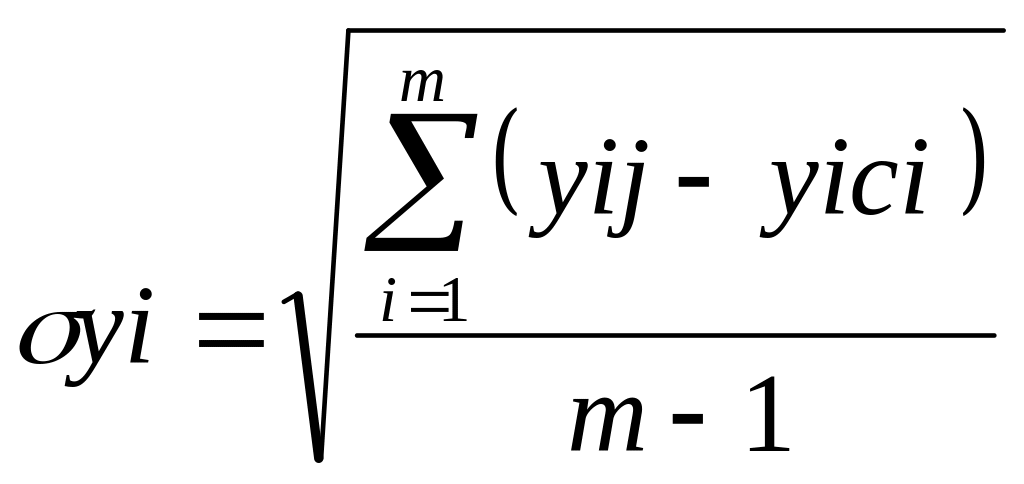(8.12)

где , m – число повторных замеров.

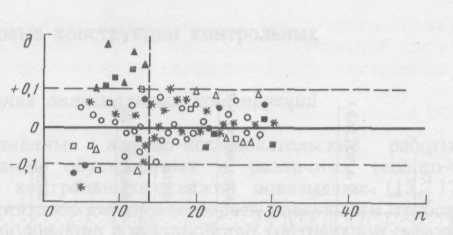
Рисунок 8.2 - Распределения фактических погрешностей воспроизводимости повтор­ных замеров σ_В при измерении объема исходных выборок для методов: а - КС (градиент-зонд с АО=2,25м);

б - БМ; в - ГМ; г - НМ; д - AM (ΔТ)

После несложных преобразований, приведенных в работе, получаем окончательное выражение для определения числа повторных замеров в опорном пласте или точке:

(8.13)

В соответствии с этим выражением, оценка показате­лей качества измерений с 10%-ной погрешностью и вероят­ностью 90% осуществляется при проведении трех-четырех повторных замеров. При наличии систематических погрешностей число повторных замеров должно увеличиться в раз.

На последнем этапе обработки данных повторных измерений в контрольных скважинах должна оцениваться пригодность контро­лируемых приборов к дальнейшей работе. Она осуществляется проверкой выполнения условия , где σх_В - фактическая погрешность воспроизводимости пара­метра контролируемым прибором; σ_ДОП - допустимая для данного типа аппаратуры относительная погрешность измерений.

Задание:

1. Определите необходимый объем выборки n при вероятности Ф=95 %, гарантийном коэффициенте t =1,50 и допустимой погрешности статистических оценок 8 %.

2. Проанализируйте пути уменьшения выборки хотя бы за 40 отсчетов.

Контрольные вопросы:

1. Изложите необходимость определения качества скважинных измерений.

2. Дайте определение контрольно- поверочным скважинам.

3. Изложите понятие аддитивных σ_А, и мультипликативных σ_М составляющих погреш­ностей.

4. Дайте разъяснение по рис 8.2 распределению фактических погрешностей воспроизводимости повтор­ных замеров σ_В при измерении объема исходных выборок.