Глава 4. Деревья

Важнейший подкласс класса связных графов составляют связные графы с минимальным количеством ребер. Эти графы получили название деревьев благодаря своему структурному сходству с обычными деревьями. Термин дерево для обозначения графа специального типа впервые был использован в конце XIX в. Г. Кирхгофом для описания предложенных им методов расчета электрических цепей. Затем, решая задачу перечисления всех возможных соединений углерода и водорода, А. Кэли независимо использовал тот же термин и исследовал простейшие свойства деревьев, в частности, вывел хорошо известную формулу для числа всех деревьев данного порядка.

Деревья появляются в многочисленных приложениях в качестве составных частей моделей изучаемых явлений, и в то же время играют важную роль в современной теории графов.

Одной из наиболее популярных задач, возникающих в приложениях, является задача о построении остовного дерева минимального веса для заданного связного взвешенного графа. Эта задача и ее модификации рассматриваются в § 3 и § 4 настоящей главы. В § 1 и § 2 соответственно приводятся различные характеризации дерева и описан алгоритм Прюфера, позволяющий перечислить все деревья данного порядка.

0. § 1. Определение дерева

Минимальность деревьев в классе связных графов можно охарактеризовать различными способами, делая акцент на тех или иных особенностях ее проявления. Каждая из приводимых в теореме 4.1 характеризаций может быть принята в качестве определения дерева. В данном параграфе – неориентированный граф, – число вершин (порядок) графа , – число ребер.

Предложение 4.1. Если – связный граф, то .

Доказательство. Если , то , доказываемое неравенство выполняется как равенство. Предположим, что . Зафиксируем произвольную вершину и рассмотрим разбиение множества вершин на два подмножества: и . Обозначим через пустое множество. Поскольку граф связен, существует ребро , один конец которого , а другой . Обновим наши множества следующим образом:

. (4.1)

Если множество не пусто, то опять найдется ребро , для которого , , и процедуру обновления (4.1) можно повторить.

Поскольку изначально , то процедура (4.1) может быть выполнена раз. В результате, множество будет содержать ребро, следовательно, .

Следствие 4.1. Если , то содержит цикл.

Доказательство. Если – связный граф и , то после завершения процедуры (4.1) найдется ребро . Из построения множества следует, что после каждой итерации граф является связным. Следовательно, найдется путь , состоящий из ребер множества , концами которого являются вершины и . Присоединяя к этому пути ребро , получим цикл. Если граф не является связным, то из условия следует, что в нем найдется компонента связности, в которой число ребер не меньше числа вершин. Поэтому найдется цикл из ребер, принадлежащих этой компоненте.

Следствие 4.2. Пусть связный граф. Следующие утверждения эквивалентны.

,

не содержит циклов.

Доказательство. Импликация непосредственно вытекает из предложения 4.1 и следствия 4.1. Поскольку удаление ребра из цикла не приводит к увеличению числа компонент связности, то, предположив, что в графе имеется цикл, из предложения 4.1 мы имели бы оценку , которая противоречит условию . Поэтому импликация также имеет место. ■ 

Напомним, что в связном графе, по определению связности, любые две различные вершины могут быть соединены путем. Если такой путь не является простой цепью, т. е. некоторая вершина встречается в нем более одного раза, то, очевидно, удалив часть пути между первым и последним появлением этой вершины на пути, получим путь с теми же концами, но в котором данная вершина встречается только один раз. Следовательно, любые две вершины могут быть соединены простой цепью. Если в графе найдутся две простых цепи с общими концами, то их конкатенация будет циклом, т. е. условие (b) будет нарушено. Таким образом, условие (b) вместе с условием связности графа эквивалентно следующему условию.

Любые две различные вершины в графе могут быть соединены единственной простой цепью.

Напомним также, что в теории графов мостом называется ребро, удаление которого приводит к увеличению числа компонент связности графа. В доказательстве следствия 4.2 мы использовали тот факт, что ребро, принадлежащее циклу, не является мостом. Очевидно, справедливо и обратное утверждение: если некоторое ребро не входит ни в один цикл, то оно является мостом. Поэтому условие эквивалентно следующему условию.

Любое ребро в графе является мостом.

В итоге мы получаем теорему.

Теорема 4.1. Следующие утверждения эквивалентны:

– связный граф и ;

– связный граф без циклов;

Любые две различные вершины в графе могут быть соединены единственной простой цепью;

– связный граф, в котором каждое ребро является мостом.

Определение 4.1. Граф , удовлетворяющий условию теоремы 4.1, называется деревом.

Замечание 4.1. Чаще всего в литературе деревом называют связный граф без циклов, т. е. в качестве основного берут утверждение (bb).

Определение 4.2. Граф, у которого компоненты связности являются деревьями, называется лесом.

Определение 4.3. Ориентированный граф называется ориентированным деревом (ордеревом), если:

1) существует ровно одна вершина называемая корнем, которая не имеет предшествующих: ;

2) любой другой вершине непосредственно предшествует ровно одна вершина: .

Замечание 4.3. Неориентированное дерево можно превратить в ориентированное, выбрав в качестве корня произвольную вершину. При этом ориентация ребер исходного дерева определяется однозначно. На рис. 4.1. приведен пример ориентации дерева. Очевидно, что любое ориентированное дерево можно рассматривать как результат ориентации обычного дерева, полученной в результате выбора корня. Поэтому ориентированные деревья называют также корневыми.

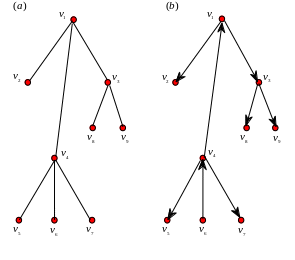
Рис. 4.1. Ориентация дерева. (а) Неориентированное дерево. (б) Ориентация дерева, в которой в качестве корня выбрана вершина .