§ 3. Классы р и np

Классом Р называется класс распознавательных задач, каждая из которых может быть решена с помощью некоторого алгоритма за полиномиальное время (для которой может быть построена МТ, имеющая полиномиальное время работы). К таким задачам относятся задачи построения кратчайших путей (см. гл. 3), минимального остова (см. гл. 4), наибольшего паросочетания и др.

Классом NP называется класс распознавательных задач, каждая из которых может быть решена с помощью некоторого недетерминированного алгоритма за полиномиальное время (для которой может быть построена НМТ, имеющая полиномиальное время работы). Задачи, принадлежащие классу NP, называют «трудными».

Так как всякая детерминированная МТ представляет собой недетерминированную МТ, у которой нет возможности выбора переходов, то

.

При этом класс NP чрезвычайно широк, и в нем содержится множество задач, для которых не доказана их принадлежность к классу P. В качестве примера можно привести задачу об изоморфизме графов.

Даны два графа: и . Необходимо определить, являются ли они изоморфными, т. е. установить, существует ли отображение такое, что истинны следующие импликации: и .

Вторым примером может служить следующая задача. Даны граф G и натуральное число k. Определить, содержит ли граф G клику мощности k. Для этих и многих других в пока не найдено полиномиальных алгоритмов решения.

До сих пор остается не решенным фундаментальный вопрос теории алгоритмов, совпадают ли классы Р и NP? Другими словами, можно ли утверждать, что для задач, не имеющих полиномиальных алгоритмов решения, но являющихся NP-трудными, эти решения существуют и просто пока не найдены, или таких алгоритмов не существует.

Если окажется, что , то это означает, что ни одна из «трудных» задач не имеет полиномиального решения. Кроме того, если такой алгоритм существует хотя бы для одной из подобных задач, то верно равенство и все «трудные» задачи имеют полиномиальные алгоритмы решения.

Глава 3. Экстремальные пути в графах

В данной главе рассматриваются задачи нахождения кратчайших и наиболее длинных путей в графах. Такие задачи имеют многочисленные приложения в разных областях, в частности, в задачах управления. Рассматриваемые в данной главе алгоритмы можно найти, например, в [3, 4, 22].

Для того чтобы применять различные алгоритмы для решения задач на графах необходимо иметь удобное представление этих графов в компьютере. Данный вопрос рассматривается в следующем разделе.

§ 1. Хранение графов в памяти компьютера

Известны различные способы представления графов в компьютере. Нужный способ выбирается в соответствии с потребностями конкретной задачи.

Будем предполагать, что каждое число независимо от его вида занимает в памяти компьютера одну ячейку.

Проиллюстрируем некоторые способы такого представления на примере графов, приведенных на рис. 3.1 и 3.2.

Рис. 3.1. Граф . Рис. 3.2 Орграф .

• Представление графов с помощью матрицы смежности.

Матрицей смежности графа называется квадратная матрица порядка . Для неориентированных графов

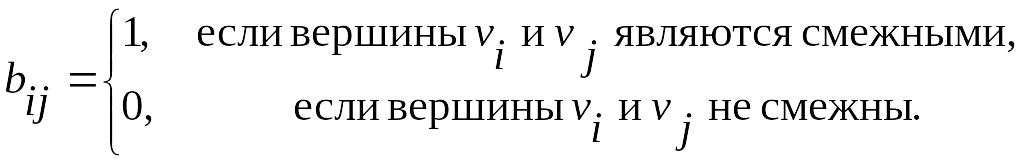
Для орграфов

Тогда для графа матрица смежности будет иметь вид

,

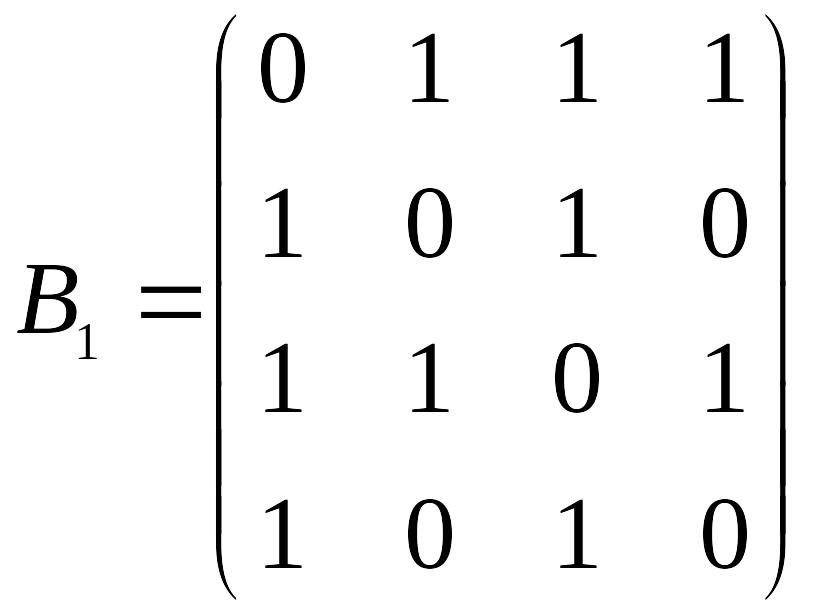а для графа –

.

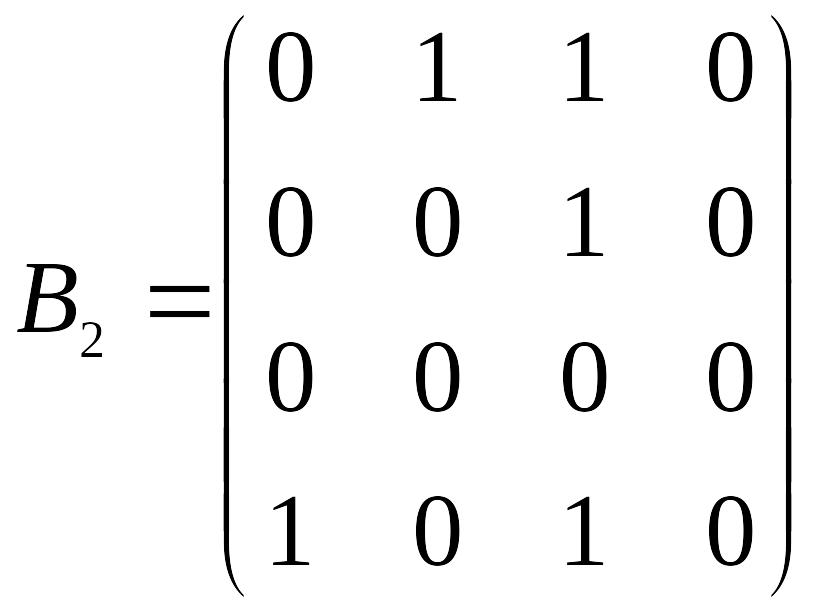Такое представление требует ячеек памяти.

Заметим, что для неориентированных графов матрица смежности симметрична относительно главной диагонали, поэтому достаточно хранить только верхнюю или нижнюю треугольную матрицу. Тогда потребуется ячеек памяти.

• Представление графов с помощью матрицы инцидентности.

Матрица инцидентности – это матрица размера , т. е. число строк равно числу вершин, число столбцов – числу ребер. Для неориентированного графа

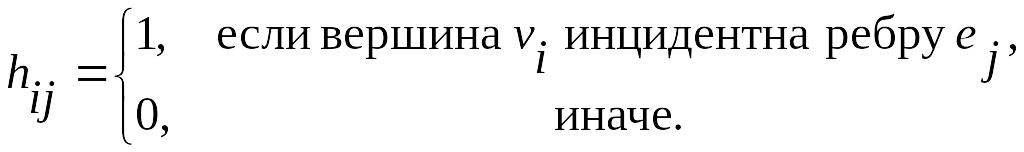
Для ориентированного графа

Такое представление требует ячеек памяти.

Заметим, что для того чтобы составить матрицу инцидентности необходимо перенумеровать все ребра графа.

Тогда для графа матрица инцидентности будет иметь вид

а для графа –

• Списки смежности.

Графы можно представить с помощью списочной структуры, показывающей смежность вершин. Создается массив указателей, содержащий все вершины графа, на списки смежных вершин.

Для графа имеем

а для графа –

Такое представление требует для неориентированных графов ячеек памяти, для орграфов – ячеек.

• Представление сетей.

Сети представляют в виде квадратной матрицы порядка где

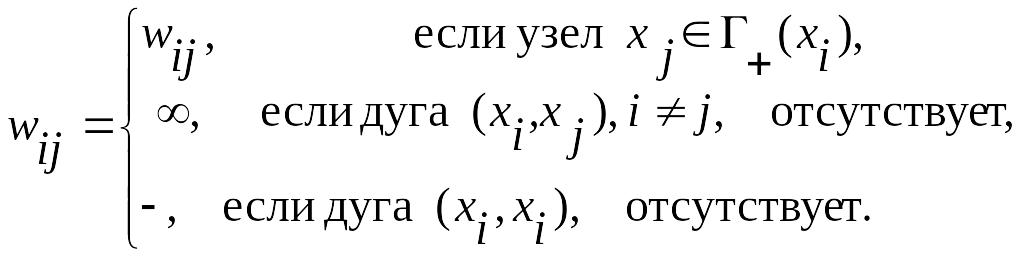
Замечание 3.1. Вместо символа «∞» чаще всего задают самое большое возможное число, а вместо символа « – » некоторое число в зависимости от условий решаемой задачи.

Рассмотрим сеть

Рис. 3.3. Сеть .

Тогда матрица А будет иметь вид

.