
- •Глава 1. Основные понятия теории графов
- •§ 1. Основные определения
- •§ 2. Виды графов
- •§ 3. Примеры приложений теории графов
- •§ 4. Изоморфизм графов
- •§ 5. Степень вершины
- •§ 6. Подграфы, операции над графами
- •Соединением графов называется граф , в котором , а множество ребер состоит из всех ребер и
- •§ 7. Маршруты, цепи, циклы
- •§ 8. Метрические и топологические характеристики графов
- •§ 9. Связность в орграфах
- •Глава 2. Алгоритмы § 1. Сложность алгоритмов
- •§ 2. Машины Тьюринга
- •§ 3. Классы р и np
- •Глава 3. Экстремальные пути в графах
- •§ 1. Хранение графов в памяти компьютера
- •§ 2. Алгоритмы построения кратчайших путей
- •2.1. Алгоритм Дейкстры
- •2.2. Алгоритм Беллмана – Форда построения дерева кратчайших путей для сети с произвольными весами
- •§ 3. Задача о максимальном пути
- •Алгоритм построения максимального пути для сети с введенным топологическим порядком.
§ 6. Подграфы, операции над графами
Определение
1.12. Граф
![]() называется подграфом
графа
называется подграфом
графа
![]() ,
если
,
если
![]() и
и
![]() .
.
Если
![]() или
или
![]() ,
то граф
,
то граф
![]() называется
собственным
подграфом
G.
называется
собственным
подграфом
G.
Если
![]() ,
то
называется остовным
подграфом G.
,
то
называется остовным
подграфом G.
Подграф называется правильным подграфом G, если он содержит все возможные ребра G.
Полный подграф называется кликой графа G.
Граф G приведен на рис. 1.14
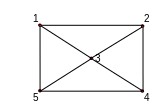
Рис. 1.14. Граф с пятью вершинами.
На рис. 1.15 – 1.19 изображены различные подграфы графа G:
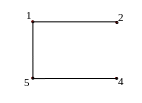
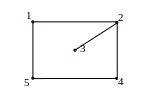 Рис.
1.15. Собственный неправильный
Рис. 1.16. Остовной неправильный
Рис.
1.15. Собственный неправильный
Рис. 1.16. Остовной неправильный
подграф. подграф.

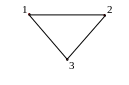
Рис. 1.17. Правильные подграфы.
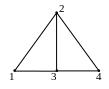
Рис. 1.18. Клика графа G.
Определение
1.13. Дополнением
графа
называется граф
с тем же множеством вершин
,
в котором любые две вершины смежны тогда
и только тогда, когда они не смежны в
исходном графе G,
обозначается
![]() .
.
На рис. 1.19 изображен граф, являющийся дополнением к графу G, представленному на рис. 1.14:

Рис. 1.19. Дополнение к графу G.
Рассмотрим следующие операции над графами:
Объединением графов
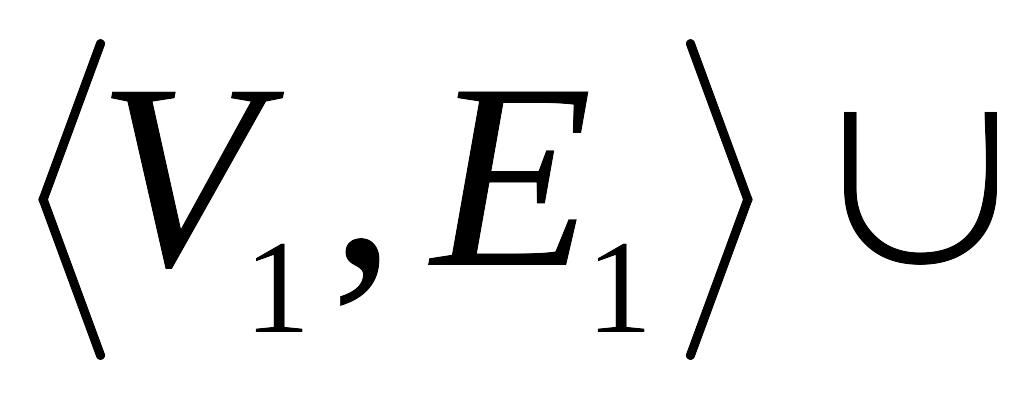
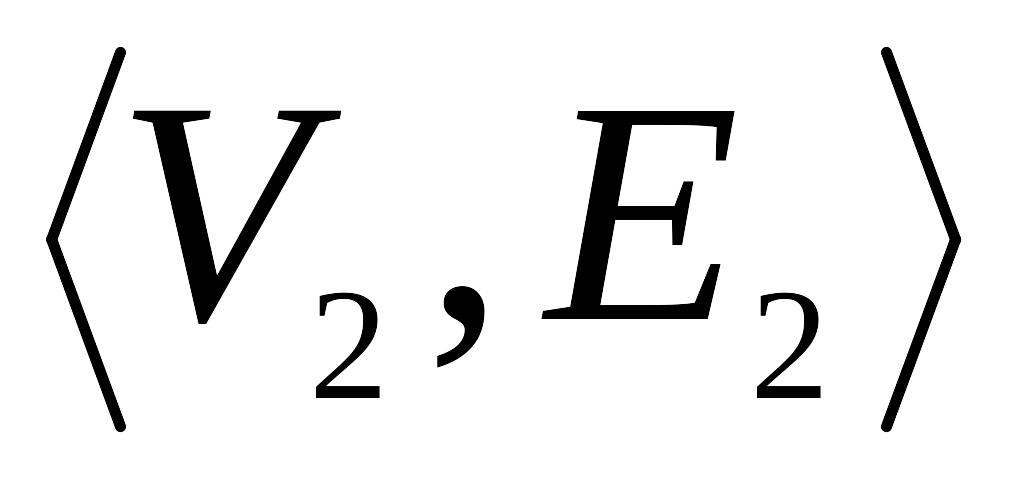 с непересекающимися множествами вершин
(
с непересекающимися множествами вершин
(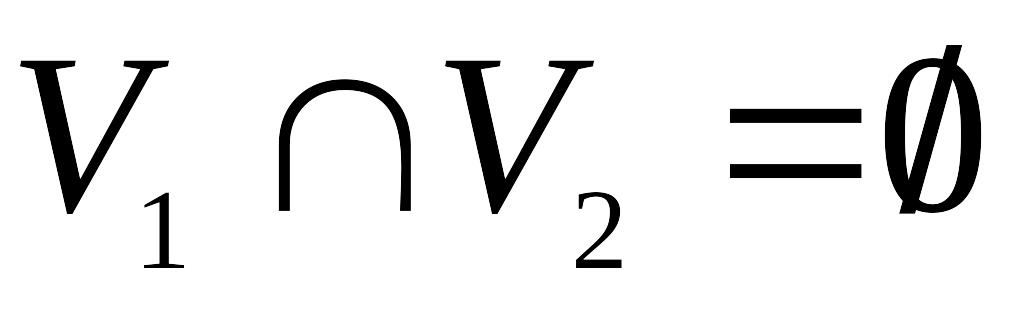 )
называется граф
)
называется граф
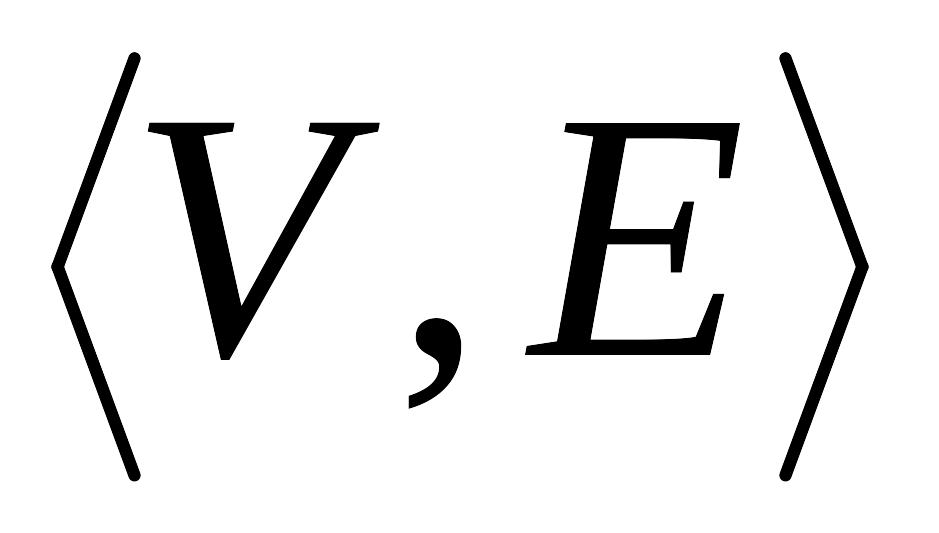 ,
в котором множество вершин и множество
ребер образованы соответственно
объединением множеств вершин и ребер
графов, входящих в объединение:
,
в котором множество вершин и множество
ребер образованы соответственно
объединением множеств вершин и ребер
графов, входящих в объединение:
![]() .
.
Соединением графов называется граф , в котором , а множество ребер состоит из всех ребер и
и всех ребер,
соединяющих вершины из
![]() с вершинами из
:
с вершинами из
:
![]() .
.
Графы
![]() и
и
![]() приведены на рис. 1.20, а
и 1.20, б
соответственно.
приведены на рис. 1.20, а
и 1.20, б
соответственно.
а: б:
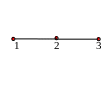

Рис. 1.20. Неориентированные графы.
На рис. 1.21 и 1.22 приведены иллюстрации различных операций над графами:
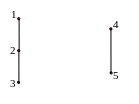
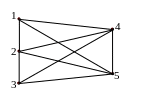
Рис. 1.21. Объединение графов
![]() и
и
![]() .
Рис. 1.22. Соединение графов
и
.
.
Рис. 1.22. Соединение графов
и
.
Удаление вершины v из графа приводит к графу
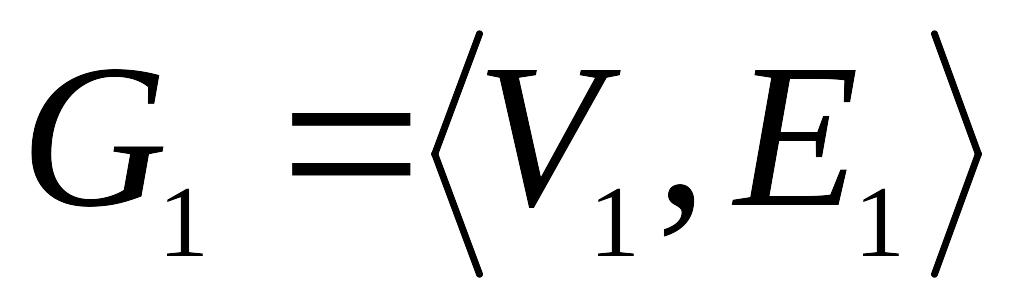 (обозначается
(обозначается
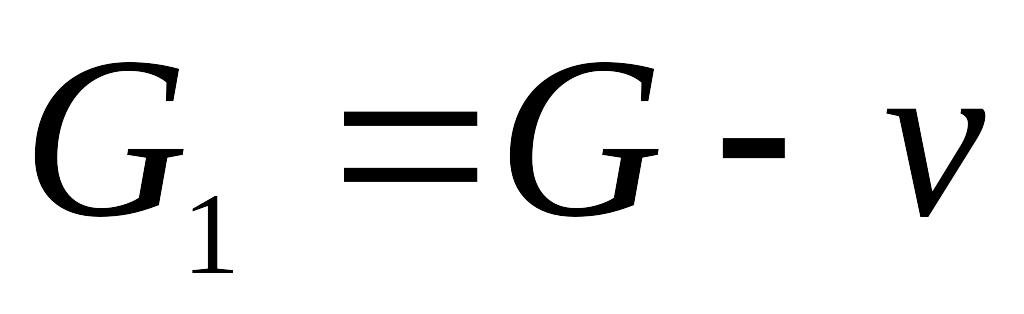 ),
содержащему все вершины исходного
графа кроме удаленной вершины v
и все ребра, кроме инцидентных удаленной
вершине:
),
содержащему все вершины исходного
графа кроме удаленной вершины v
и все ребра, кроме инцидентных удаленной
вершине:
![]() .
.
Пример 1.7.
Рассмотрим граф G
на рис.1.14. Его клика, изображенная на
рис. 1.18, получена из исходного графа
путем удаления вершины {5}:
![]() .
.
Заметим, что при удалении вершины всегда получается правильный подграф.
Удаление ребра e из графа G дает остовной граф
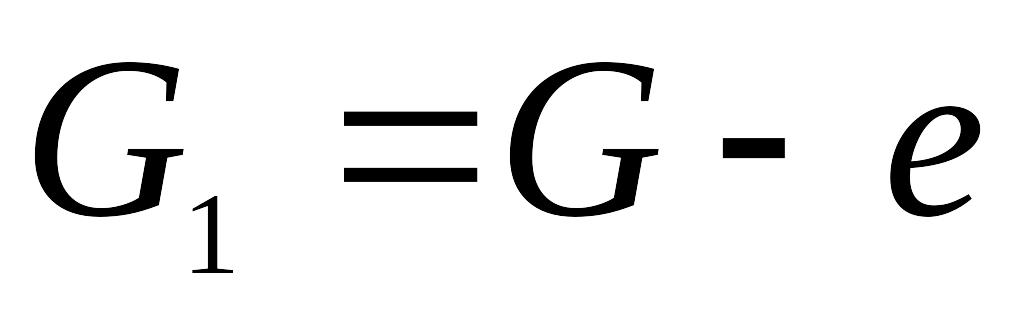 ,
содержащий все ребра кроме ребра e.
,
содержащий все ребра кроме ребра e.Добавление вершины v в граф G приводит к графу , являющимся объединением G и графа
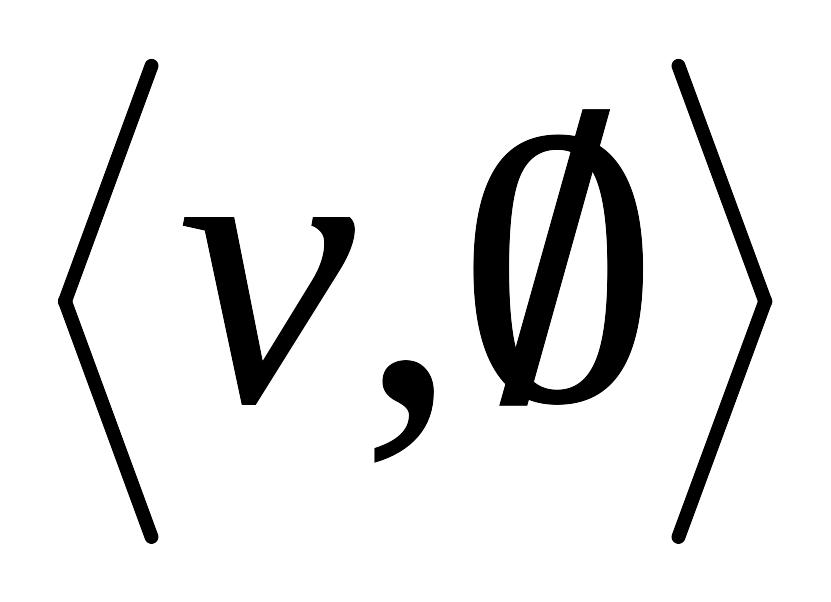 :
:
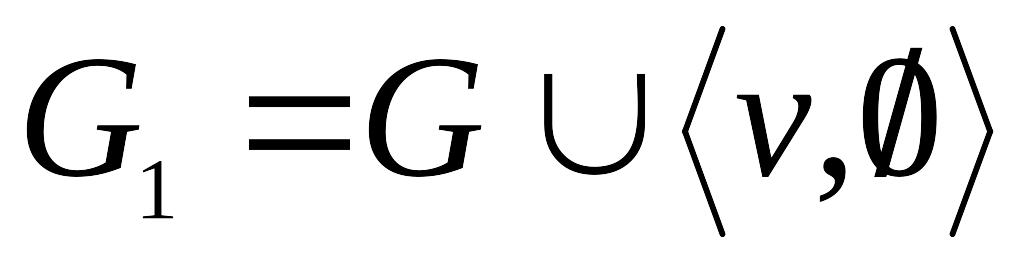 (обозначается
(обозначается
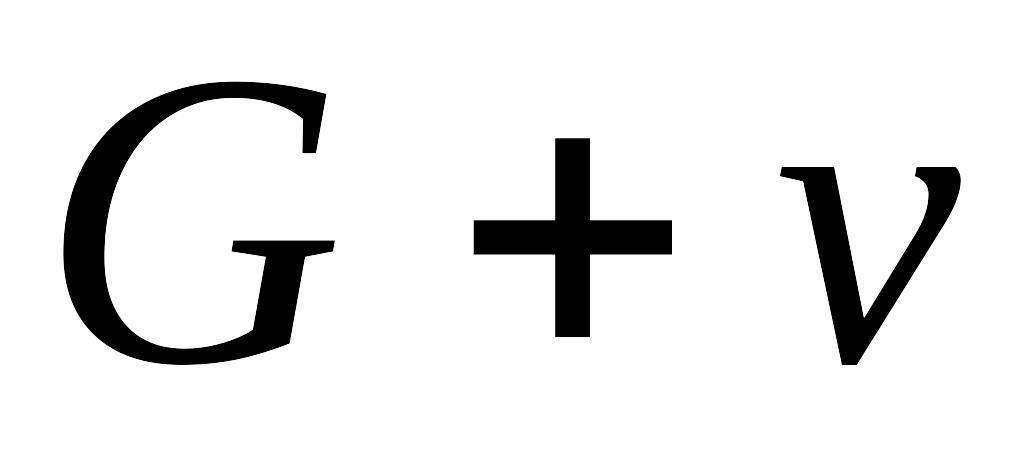 ).
).Добавление ребра e в граф G дает граф
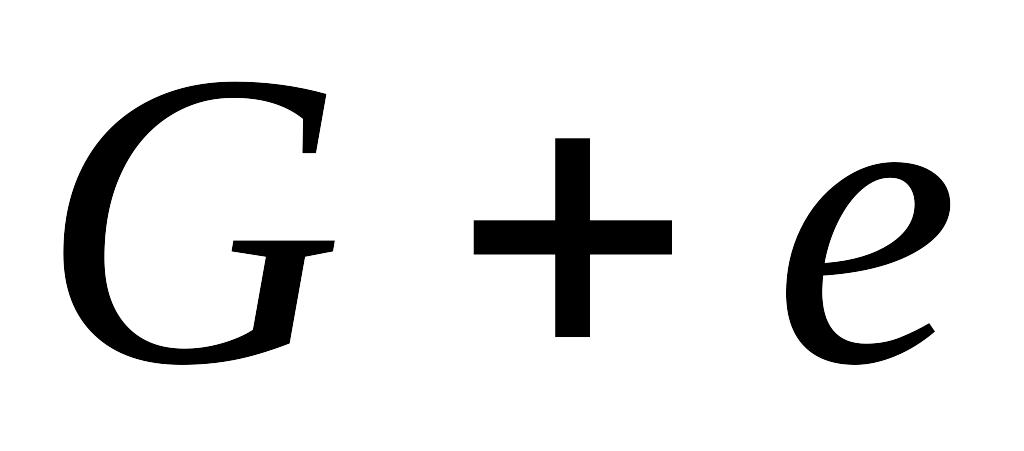 ,
во множество ребер которого добавлено
ребро е.
,
во множество ребер которого добавлено
ребро е.
На рис. 1.23 – 1.27 проиллюстрированы операции над графами:
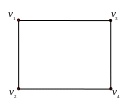
Рис. 1.23. Граф G.
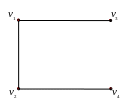
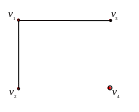
Рис. 1.24. Граф
![]() .
Рис. 1.25. Граф
.
Рис. 1.25. Граф
![]() .
.
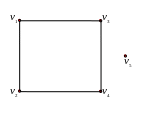
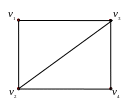
Рис. 1.26. Граф
![]() .
Рис. 1.27. Граф
.
Рис. 1.27. Граф
![]() .
.
