Глава 1. Основные понятия теории графов

Теория графов начала развиваться с выходом работы Эйлера, написанной им в 1736 г. Поначалу эта теория считалась незначительным и даже шутейным разделом математики, так как, с ее помощью решались в основном математические головоломки. Однако со временем графы нашли широкое применение во множестве различных областей знаний, например, их стали использовать в физике, химии, биологии, медицине, генетике, лингвистике, экономике и т.д. Для более глубокого ознакомления с теорией графов читателю рекомендуется монографии [1 – 3, 8, 10, 11, 13, 14].

§ 1. Основные определения

Рассмотрим непустое множество , , и множество E, состоящее из неупорядоченных пар элементов множества V:

,

кроме того .

Определение 1.1. Графом (неориентированным графом) называется совокупность двух множеств – непустого множества вершин V и множества ребер E.

В дальнейшем число вершин графа G будем обозначать , а число ребер – m ( ), и говорить, что G определяет (n, m) граф, где n – порядок графа, а m – размер.

Рассмотрим непустое множество , , и множество A, состоящее из упорядоченных пар элементов множества A:

,

кроме того, .

Определение 1.2. Ориентированным графом или орграфом называется совокупность двух множеств – непустого множества узлов (или вершин) X и множества дуг А.

Основанием орграфа называется неориентированный граф с теми же вершинами, в котором все дуги заменены на ребра.

Замечание 1.1. Если дуга , то говорят, что – начало дуги, а – конец.

Определение 1.3. Говорят, что вершина и ребро инцидентны, вершина и ребро также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными. Множество вершин, смежных с вершиной v, называется окружением этой вершины и обозначается :

.

Для орграфов , где – множество узлов, непосредственно следующих за узлом x, – множество узлов, непосредственно предшествующих узлу x.

Обычно графы представляют диаграммой, вершинам которой соответствуют точки или кружки, а ребрам – линии. Дуги орграфа изображают стрелками, направление которых соответствует направлению дуги.

Диаграмма неориентированного графа, в котором вершины и , и , и , и – смежные, вершины и не являются смежными; ребра и , и , и – смежные; ребро инцидентно вершинам и , изображена на рис. 1.1.

На рис.1.2 изображена диаграмма орграфа, в котором , . Граф на рис.1.1 является основанием для орграфа, изображенного на рис.1.2.

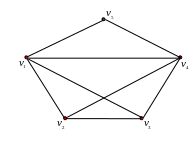
Рис. 1.1. Неориентированный граф.

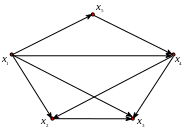
Рис. 1.2. Орграф.

Примером графа является схема железных дорог. При этом вершинами его выступают станции, а ребрами перегоны между ними. На рис.1.3 приведена карта-схема основных железнодорожных магистралей в окрестности Санкт-Петербурга.

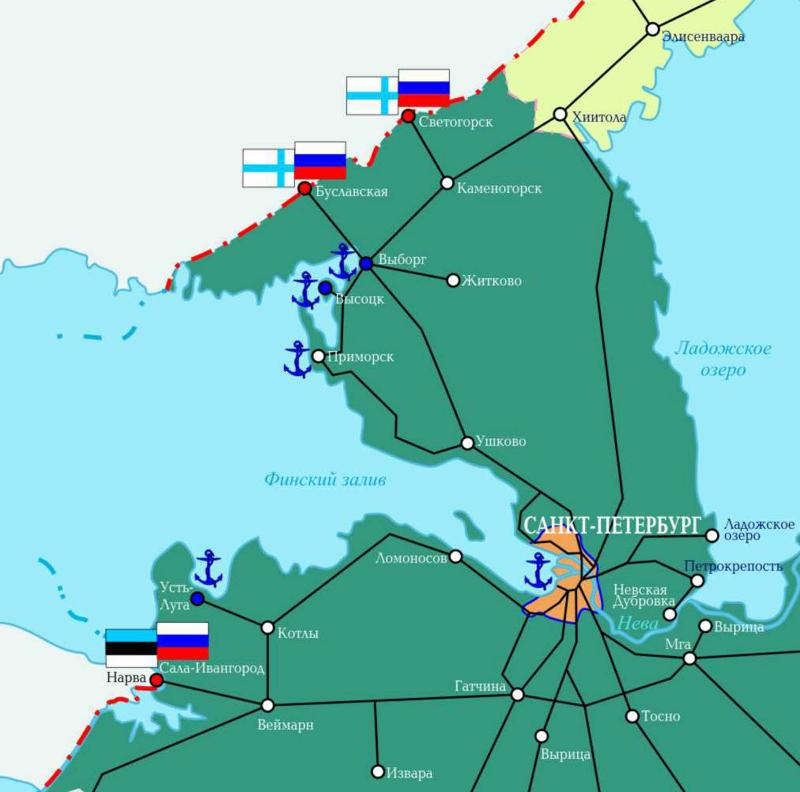
Рис. 1.3. Карта-схема основных железнодорожных магистралей

в окрестности Санкт-Петербурга.

§ 2. Виды графов

Определение 1.4. Граф, состоящий из одной вершины, называется тривиальным.

Определение 1.5. Граф, в котором каждая вершина соединена с каждой, называется полным. Полный граф с n вершинами обозначается (рис. 1.4).

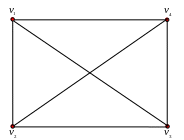
Рис. 1.4. Полный граф с четырьмя вершинами.

Полный граф имеет максимально возможное число ребер:

.

Определение 1.6. Если каждой дуге орграфа сопоставлена некоторая величина , т.е. на дугах орграфа задана вещественная функция , то граф G называется графом со взвешенными узлами или сетью, и обозначается . Величина называется весом дуги .

Пример 1.5. На рис. 1.5 изображена сеть, у которой веса дуг имеют следующие значения: .

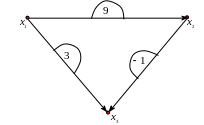
Рис. 1.5. Сеть.

Определение 1.7. Двудольным графом называется граф , такой что множество V разбито на два непересекающихся множества и ( ), причем всякое ребро из E инцидентно вершине из и .

Таким образом, в двудольном графе каждое ребро соединяет вершины из с вершинами из . Заметим, что не обязательно каждая вершина первого множества связана с каждой вершиной второго. Если это условие выполнено, то такой граф называется полным двудольным графом.

Пример 1.6. Рассмотрим следующую ситуацию. Пусть имеются несколько различных вакансий и группа лиц, стремящихся их занять, причем каждый из претендентов обладает достаточной квалификацией для нескольких, но, вообще говоря, не для всех имеющихся вакансий. Обозначим множество лиц , а множество вакансий . Каждого человека из множества можно соединить с вакансиями из множества , при этом никакие две вершины из и никакие две вершины из не окажутся смежными.

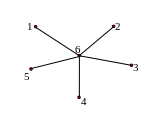
Рис. 1.6. Два претендента и три вакансии. Рис. 1.7. Пять претендентов на

одну вакансию.

Определение 1.8. Граф, у которого элементом множества E может быть пара одинаковых элементов V, называется графом с петлями (рис.1.8), а сам элемент – петлей.

Если Е является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называют кратными ребрами, а граф – мультиграфом (рис.1.9).

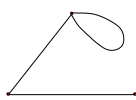
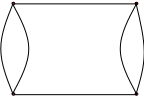
Рис. 1.8. Граф с петлей. Рис. 1.9. Мультиграф.