2. Загальне середнє арифметичне

_{Припустимо, що в результаті вимірів однієї величини отримано статистичний ряд нерівноточних результатів}

_{. (6.53)}

_{Найкращі оцінки отримують тоді, коли виміри хі або їх похибки і, підкоряються нормальному закону розподілу.}

_{Перейдемо до нормованих похибок}

_{; , ..., , (6.54)}

_{де Х – істинне значення вимірюваної величини.}

_{Функція щільності нормованого нормального закону розподілу визначається за формулою}

_.

_{Числові характеристики визначаються за результатами всіх вимірів. Тоді функція щільності сумісного розподілу ряду випадкових величин t1, t2, …, tk буде}

_{. (6.55)}

_{Найбільш надійне значення шуканого параметра t для нерівноточних вимірів буде відповідати максимальному значенню функції  (t1, t2, …, tn). Із формули (6.55) видно, що це відбудеться за умови, коли показник степеня буде мінімальним, тобто}

_{. (6.56)}

_{З врахуванням формули (6.54) отримаємо}

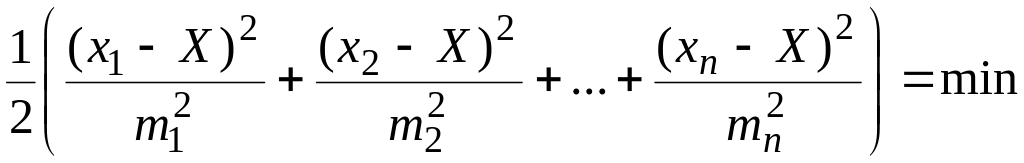_{. (6.57)}

_{Для визначення екстремуму функції (6.57) візьмемо першу похідну за перемінними хі, прирівняємо до нуля і отримаємо}

, (6.58)

Умовно помножимо їх на довільне число С, отримаємо

_{. (6.59)}

_{Оскільки , то отримаємо}

_{[xp] – X [p] = 0. (6.60)}

_{Ймовірно .}

_{Це означає, що частка при необмеженій кількості вимірів прямує до істинного значення. Його називають загальним середнім арифметичним}

_{, (6.61)}

_{або . (6.62)}

_{В разі рівноточних вимірів р1 = р2 = ... = рп = 1, а [p] = n.}

_{Тоді формула (6.61) зводиться до простої арифметичної середини}

_,

_{тому формулу (6.61) і називають загальною середньою арифметичною.}

3. Середня квадратична похибка одиниці ваги

_{Нерівноточні виміри характеризують дисперсіями або мірою відносної точності рі. Умовно із ряду нерівноточних вимірів виберемо результат такого виміру хk, вага якого буде дорівнювати одиниці, тобто рk = 1. Дисперсію цього результату позначимо через }² _{. Тоді}

_{, (6.63)}

_{або середня квадратична похибка одиниці ваги буде дорівнювати:  = mk. Оскільки , то  = mk, або}

_{; (6.64)}

_{. (6.65)}

_{Тоді середня квадратична похибка будь-якого виміру визначиться за формулою}

_{. (6.66)}

_{При р = 1 mi =  – тобто середня квадратична похибка одиниці ваги є мірою точності того результату виміру, вага якого дорівнює одиниці.}

_{Визначимо середню квадратичну похибку одиниці ваги:}

_{а) при заданому істинному значенні виміряної величини}

_{В результаті нерівноточних вимірювань однієї і тієї ж величини Х отримано статистичний ряд}

_{, (6.67)}

_{де – істинні похибки нерівноточних вимірів,}

_{– вага вимірів.}

_{Згідно з формулою (6.52) зведемо ряд нерівноточних похибок вимірів до рівноточного ряду}

_{, . (6.68)}

_{Оскільки ряд (6.68) є рівноточним і підкоряється нормальному закону розподілу, то за формулою Гаусса (6.24) можна визначити середню квадратичну похибку m вимірів. Для виміру вага якого дорівнює одиниці р = 1. Це буде середня квадратична похибка одиниці ваги , або}

_,

_{або . (6.69)}

_{б) при обчисленому загальному середньому арифметичному}

_{Як і в рівноточних вимірюваннях використаємо формулу (6.25), тобто}

_{рі, ; . (6.70)}

_{де – загальне середнє арифметичне;}

_{Х – істинне значення вимірюваної величини.}

_{Зробимо перетворення}

_.

_{Тобто, при нерівноточних вимірах і наявності істинних похибок систематична похибка  визначиться за формулою}

_{. (6.71)}

_{Для спрощення доказів складемо ряд ймовірних похибок}

_{рі , . (6.72)}

_{Оскільки , то}

_{[pV] = 0 . (6.73)}

_{З формули (6.72) ряд імовірних похибок теж є нерівноточним. Як і в попередньому випадку зведемо їх до рівноточного вигляду}

_{, . (6.74)}

_{Оскільки ряд (6.74) є рівноточним і за умовами підкоряється нормальному закону розподілу, то за формулою Бесселя (6.34) визначимо середню квадратичну похибку m. Для виміру, вага якого буде дорівнювати одиниці (р = 1), згідно з формулою (6.65) вона буде дорівнювати середній квадратичній похибці одиниці ваги, тобто }

_,

_{або . (6.75)}

_{4. Середня квадратична похибка загального середнього арифметичного}

_{Формулу загального середньоарифметичного (6.62) отримаємо у вигляді}

_{. (6.76)}

_{За формулою (3.59) дисперсія функції F(x) при отримаємо}

_(6.77)

_{Оскільки за формулою (6.66) то формула (6.77) зведеться до вигляду}

_,

_{або . (6.78)}

_{Згідно з формулою (6.78) середня квадратична похибка загального середнього арифметичного при нерівноточних вимірах визначиться за формулою}

_{. (6.79)}

_{Додатково обчислюють:}

_{5. Середню квадратичну похибку середньої квадратичної похибки одиниці ваги}

_{. (6.80)}

_{6. Середню квадратичну похибку середньої квадратичної похибки загального середнього арифметичного}

_{. (6.81)}

7. _{При необхідності визначають середні квадратичні похибки окремих вимірів}

_{. (6.82)}

_{Відносні похибки обчислюють так само як і при рівноточних вимірах (§ 3; розд.6).}

_{Запитання для самоперевірки}

1. _{Які задачі вирішує теорія похибок вимірів?}

2. _{Які складові комплексу умов?}

3. _{Назвіть види вимірювань.}

4. _{Яка роль надлишкових вимірів?}

5. _{Назвіть види похибок вимірів.}

6. _{Яка природа виникнення випадкових похибок?}

7. _{Які виміри є рівноточними?}

8. _{Які виміри є нерівноточними?}

9. _{Що характеризує проста арифметична середина?}

10. _{Що характеризує середня квадратична похибка m?}

11. _{Що характеризує середня квадратична похибка М ?}

_{12. Які числові характеристики рівноточних вимірів Ви знаєте?}

_{13. Що таке вага виміру і як її визначити?}

_{14. Що характеризує загальне середнє арифметичне?}

_{15. Що характеризує середня квадратична похибка одиниці ваги?}

_{16. Як визначити середню квадратичну похибку нерівноточного виміру?}

_{17. Що визначає середня квадратична похибка М при нерівноточних вимірах?}

_{18. Як визначити відносні похибки?}

163