§ 4. Додавання подій. Теорема додавання ймовірностей

На практиці ми здебільшого маємо справу із складними подіями, які є результатом взаємодії елементарних подій.

Сумою декількох подій називають подію, коли при випробуваннях виникає хоча б одна з цих подій.

Суму S подій А, В, С, ..., N позначають

S = A + B + C + … + N.

Приклад 1. Подія А – вірний вимір кута в першому прийомі, подія В – теж саме в другому прийомі, то подія С – одержання вірного значення кута буде

С = А + В.

Додавання несумісних ймовірностей визначають теоремою:

Ймовірність появи однієї із декількох несумісних подій дорівнює сумі ймовірностей цих подій.

Якщо подія В складається із подій А₁, А₂, ..., А_п ,

то Р(В) = Р(А₁+ А₂+ ...+ А_п)=Р(А₁) + Р(А₂) + ...+ Р(А_п), (1.8)

або 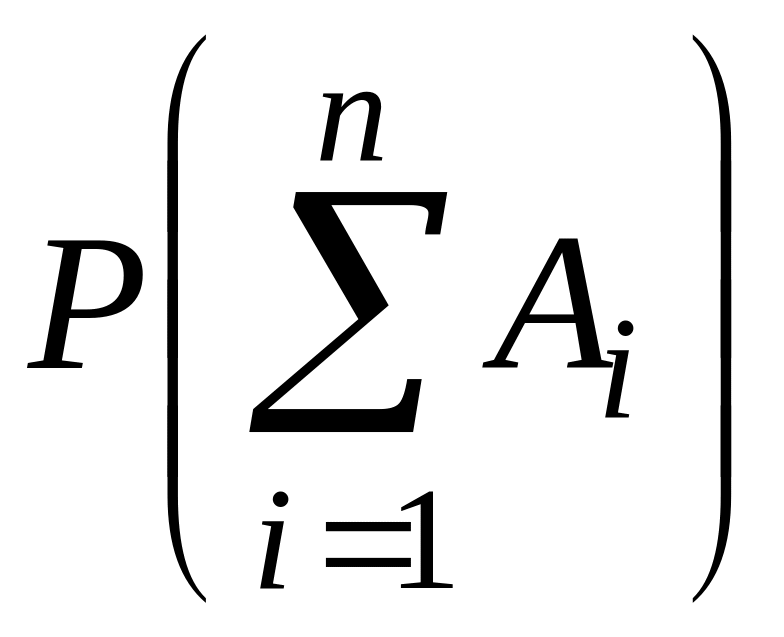= . (1.9)

Доведення. Припустимо: М₁ – число випадків сприятливих події А₁;

М₂ – число випадків сприятливих події А₂;

...........................................................................

М_п – число випадків сприятливих події А_п;

N – число всіх можливих випадків випробувань.

Згідно з формулою (1.2) маємо ймовірність кожної із елементарних подій

Р(А₁) = ; Р(А₂) = ; ... ; Р(А_п) = . (1.10)

А₁, А₂, ..., А_п несумісні, тобто нема таких подій, що сприяють їх одночасній появі, то події В сприяють В = М₁ + М₂ + ...+ М_п випадків. Тоді

Р(В) = Р (А₁ + А₂ + .... + А_п) = .

Згідно з формулами (1.10) отримаємо тотожність формулам (1.8; 1.9). Теорема доведена.

Із теореми додавання ймовірностей витікає два висновки.

Висновок 1. Якщо події А₁, А₂, ..., А_п утворюють повну групу несумісних подій, то сума їх імовірностей дорівнює одиниці

= 1. (1.11)

Доведення. Так як події А₁, А₂, ... , А_п утворюють повну групу несумісних подій, то поява хоча б одного із них – достовірна подія, тоді

Р(А₁ + А₂ + .... + А_п) = Р(А₁) + Р(А₂) + ... + Р(А_п) = ,

звідкілля = 1,

що і треба було довести.

Висновок 2. Сума ймовірностей двох протилежних подій дорівнює одиниці

Р(А) + Р( ) = 1 . (1.12)

Цей висновок витікає з висновку 1 і є його окремим випадком.

Приклад 2. На складі зберігається 100 теодолітів, із них: 20 – технічно справні, 76 – потребують перевірки та юстировки, решта – браковані. Знайти ймовірність того, що взятий навмання теодоліт можна використати в роботі.

Розв’язання. Це може статись при події А₁ – взято технічно справний теодоліт і події А₂ – взято теодоліт, який можна налагодити. Ймовірність цих подій дорівнює

Р(А₁) = = 0,20; Р(А₂) = = 0,76.

Так як ці події несумісні, то за формулою (1.8) знаходимо

Р(В) = Р(А₁) + Р(А₂) = 0,20 + 0,76 = 0,96.

Приклад 3. На топографічному плані є 80 пікетів, серед яких 6 бракованих. При контролі навмання вибирають 40 пікетів. Визначити ймовірність того, що план буде визнаний якісним, якщо допускається не більше двох бракованих пікетів серед перевірених.

Розв’язання. Позначимо через А – подію того, що при перевірці 40 пікетів не знайдеться жодного бракованого пікета, через В – подію, коли буде отримано тільки один бракований пікет і С – подію того, що буде отримано два бракованих пікети.

Події А, В і С несумісні. Згідно з умовами план буде прийнято, якщо виникне подія А + В + С. Тому за теоремою додавання ймовірностей і формулою (1.8) отримаємо

Р = Р(А) + Р(В) + Р(С).

Із 80-ти пікетів 40 можна вибрати способами, тобто N = . Із 74-х небракованих пікетів 40 пікетів можна вибрати способами, тобто М₁ = . Тоді ймовірність події А за формулою (1.2) буде

Р(А) = .

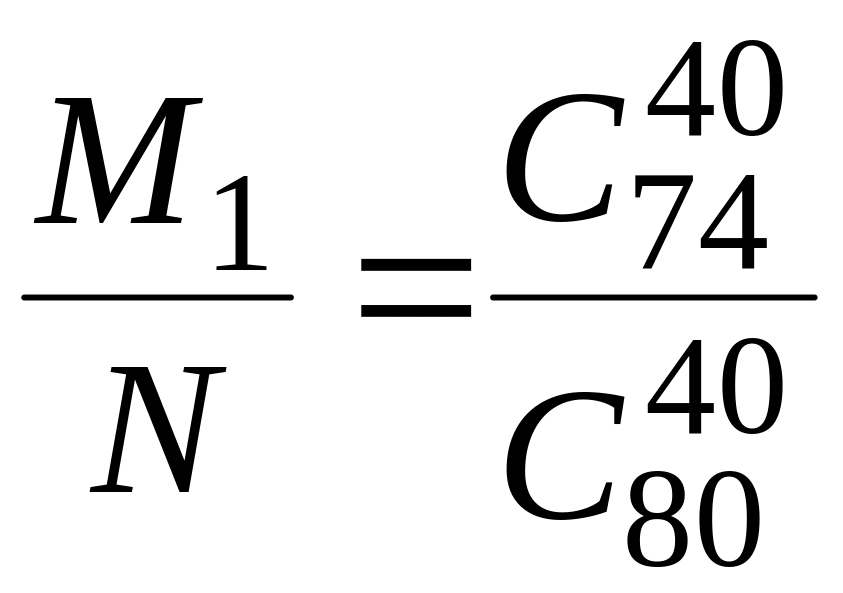Сприятливими подіями із бракованих 6-ти пікетів 1 бракований пікет може бути взятий способами, решта (40-1) пікетів не браковані і взяті із 74 пікетів системи. Тоді число сприятливих подій буде дорівнювати

М₂ = .

Отже Р(В) = .

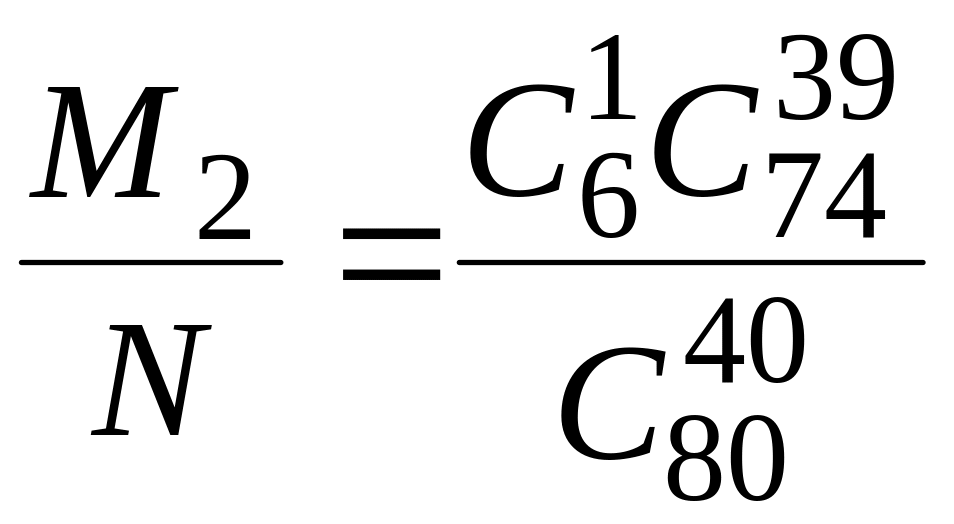Так само визначимо ймовірність події С

Р(С) = .

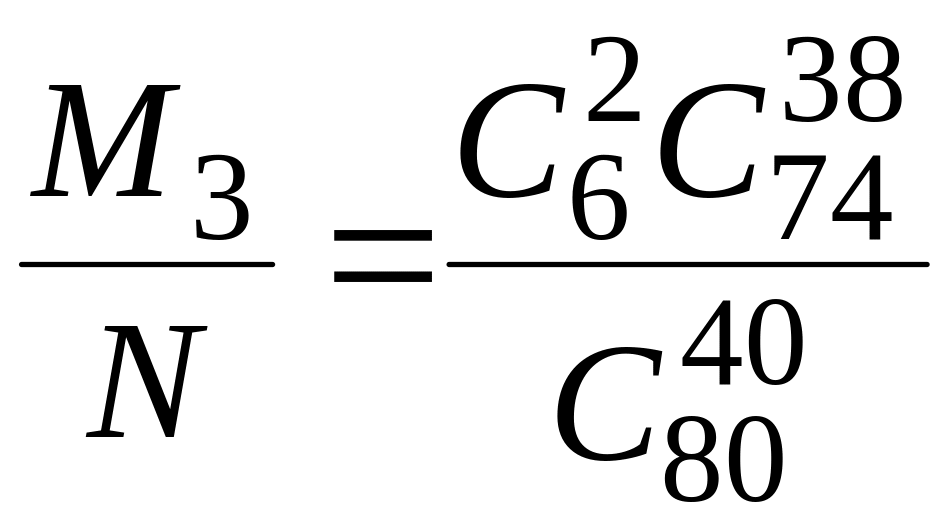Тому Р = Р(А) + Р(В) + Р(С) = 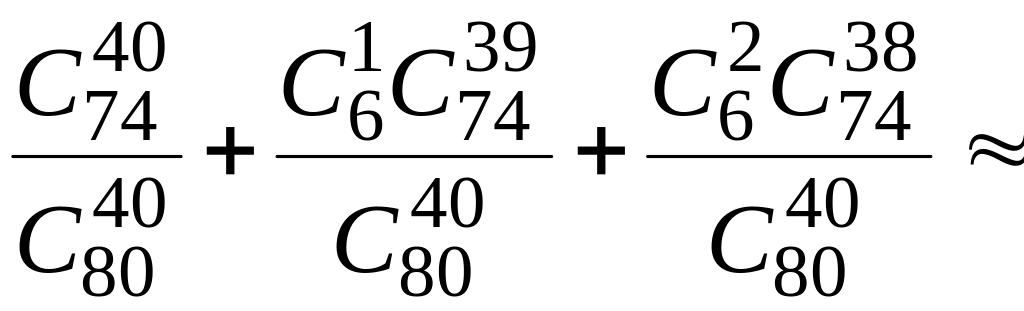0,34.