Лекція №5

За теоремою запізнення

(1)

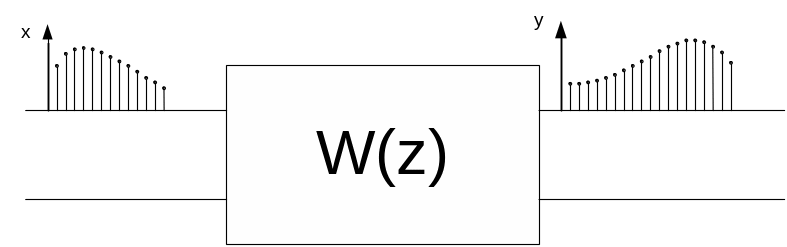[11]

Рівняння (1) дозволяє отримати значення біжучого відліку вихідного сигналу за значеннями відліків вхідного сигналу та за значеннями попередніх відліків вихідного сигналу.

На основі таких рівнянь реалізують фільтри, регулятори, та інші елементи в цифрових системах керування.

Приклад 1

Отримати різницеве рівняння елементу, який описується такою функцією передачі:

Реалізація фільтрів засобами дискретного перетворення

В аналогових системах під фільтром розуміють пристрій із спеціальною частотною характеристикою, який перетворює вхідний сигнал у вихідний, послаблюючи або підсилюючи окремі частоти в спектрі вхідного сигналу.

В цифрових системах фільтром називають елемент, що перетворює послідовність відліків вихідного сигналу у послідовність відліків вихідного сигналу усуваючи суттєві вибіги та усереднюючи значення вхідних відліків

Цифрові фільтри поділяються на дві групи:

• не рекурсивні

• рекурсивні

Не рекурсивні фільтри

Це фільтри у яких значення відліку вихідного сигналу знаходиться тільки за значеннями відліків вхідного сигналу.

Функція передачі такого фільтра можна отримати поклавши в загальні функції передачі всі коефіцієнти b_j=0 j=0…k

(2)

(3) – рівняння цього фільтра

Переваги:

Не рекурсивні фільтри мають такі переваги:

+ В наслідок відсутності зворотних зв’язків вони є абсолютно стійкими

+Існують прості способи визначення коефіцієнтів таких фільтрів

Недоліки:

Порядок не рекурсивного фільтру повинен бути вищим від порядку рекурсивного фільтра для того, щоб отримати ту ж якість фільтрування.

Приклад фільтрів (не рекурсивних)

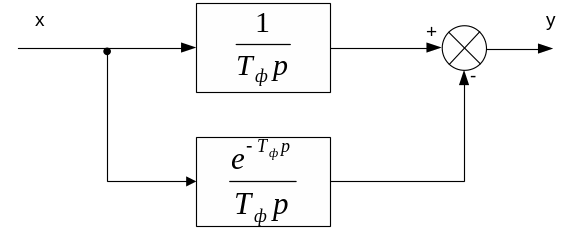
1. Фільтр ковзного середнього

Структура фільтра зображена простими аналоговими лементами

[12]

Математично роботу цього елемента можна описати

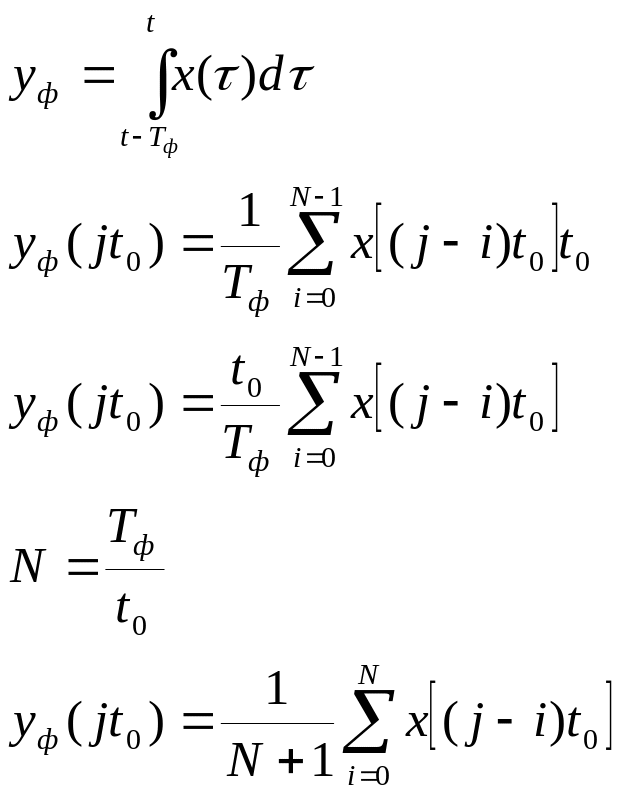
Це дискретна форма для обчислення вихідних відліків фільтра ковзного середнього

Недоліком цього фільтра є те, що необхідно для обчислення вихідного відліку в параметр N+1 вхідних відліків

Приклад 2

Статичний фільтр першого порядку.

Функція передачі цього фільтра має вигляд

(*)

Приймемо що τ рівне періоду дискретизації t₀

(**)

Із порівняння виразів * і ** видно , що елемент z^-1 відповідає формі ланці запізнення e^-t0p.

Тобто z’ це елемент затримки сигналу на один період опитування t₀

[13]

Для того, щоб отримати значення коефіцієнтів такого фільтра скористаємось першою властивістю фільтрів (M_вх=М_вих)­­

(#)

Розглянемо частковий випадок, коли тоді рівняння (#) виконується тільки при b₁=1-b₀. Кінцеве рівняння такого фільтра:

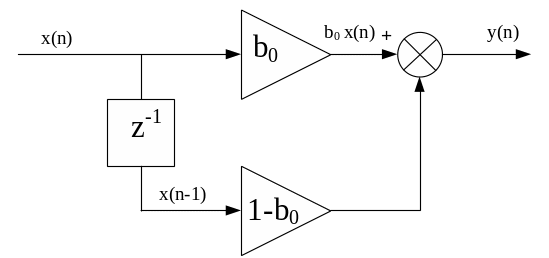
Зобразимо структурну схему цього фільтра:

[14]

Знаходження коефіцієнтів не рекурсивного фільтра за значеннями його імпульсної перехідної функції

Нехай відомі відліки скінченої І.П.Ф фільтра

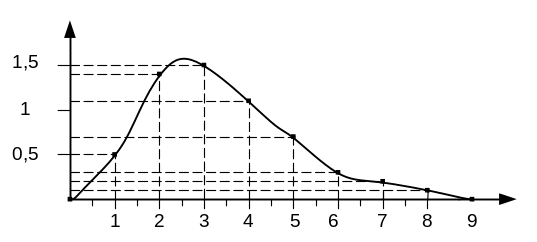[15]

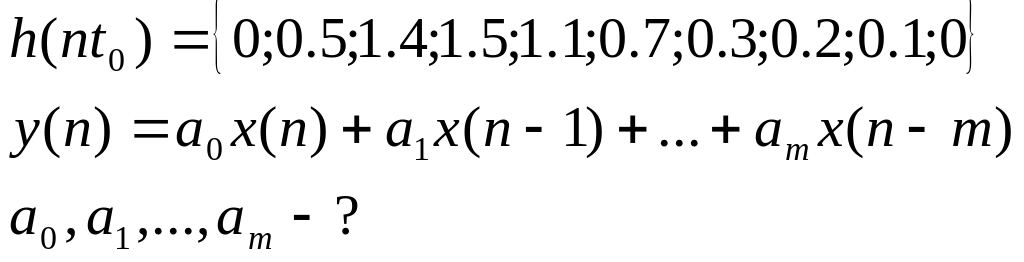
Лекція №6

Різницеве рівняння не рекурсивного фільтра в загальному випадку має такий вигляд:

(1)

Для того, щоб визначити коефіцієнти від а₀ до а_m знайдемо вихідні відліки цього фільтра за допомогою властивості згортки.

Ми отримаємо реакцію фільтра на довільний вхідний сигнал х.

(2)

Порівнюючи вирази (2) і (1) бачимо, що коефіцієнти не рекурсивного фільтра дорівнюють відповідним відлікам його імпульсної перехідної функції

Такий спосіб знаходження коефіцієнтів можна застосувати тільки для фільтрів із скінченими І.П.Ф