Математичне забезпечення асктп

Первинна обробка інформації в АСКТП

[1]

Спрощена структурна схема інформаційно вимірювального сигналу

х(t)- вимірювальна величина

z- множина неінформативних параметрів

Сигнал кожного технологічного параметра на вході АСКТП піддається певній послідовності обробки, для того , щоб отримати цифрову форму цього сигналу і подати для обробки в КЕОМ. Сукупність засобів для обробки вхідного сигналу , ліній зв’язку між ними називається інформаційно-вимірювальним каналом.

Y(t) – вихідний сигнал вимірювального перетворювача

L(t) – завада, діє на вимірювальний сигнал

Y*(t) - зашумлений сигнал технологічного параметру

БДС – блок дискретизації сигналу

Лекція №3

[2]

Під час обробки сигналу в ІВК необхідно виконати такі завдання:

1. Мінімізація впливу неінформативних параметрів (z)

2. Усунення дії завад або фільтрування сигналу для виділення його корисної складової

3. Правильний вибір періоду квантування в часі (періоду опитування) для відтворення в обчислювальній машині властивостей неперервного сигналу.

4. Правильний вибір періоду квантування за рівнем сигналу (розрядності АЦП) для зменшення похибки оцифровування сигналу

5. Знаходження проміжних значень вимірювальної величини на проміжку t₀ за допомогою методів інтерполяції та екстраполяції

Вибір кроку квантування сигналу за рівнем

Абсолютну похибку перетворення сигналу в цифрову форму можна прийняти рівною кроку квантування сигналу за рівнем

крок квантування

N – розрядність АЦП

Мінімальну розрядність АЦП,, необхідну для того, щоб похибка перетворення сигналу не перевищувала допустимої, можна отримати за формулою:

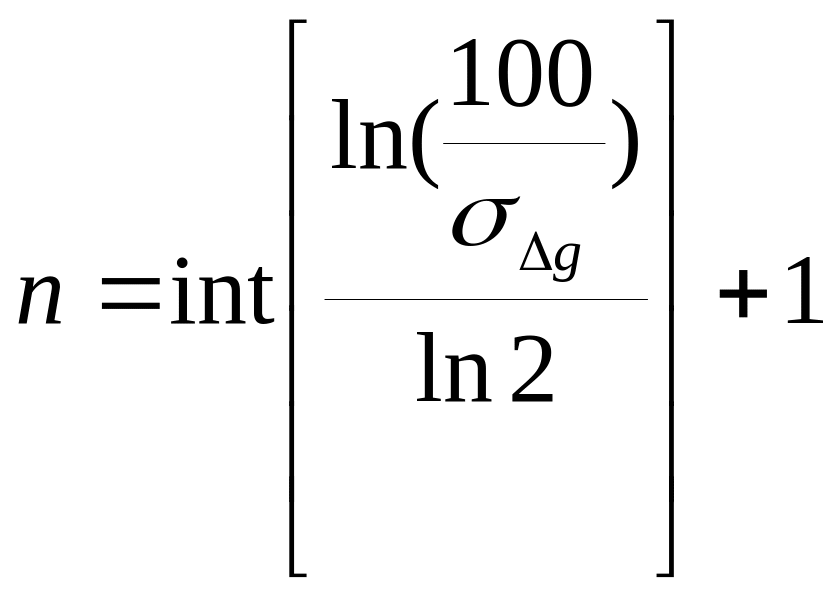
σ_Δg - допустима похибка квантування сигналу за рівнем.

Наприклад

Якщо задамо σ_Δg=0,4, то n=8

Для того, щоб отримати похибку перетворення не більшу ніж похибка сучасних вимірювальних перетворювачів технологічних параметрів необхідно застосувати АЦП із розрядністю більше 10

Вибір квантування в часі

Вибір періоду квантування в часі залежить від форми сигналу та його частотного спектру.

Існує декілька поширених способів вибору t₀ :

1. За теоремою Котельникова-Шенона Сигнал, частотний спектр якого обмежується частотою ω_зрізу може бути відновлений після дискретизації без спотворень , якщо частота дискретизації задовольняє умову.

ω₀ ≥ 2ω_зрізу

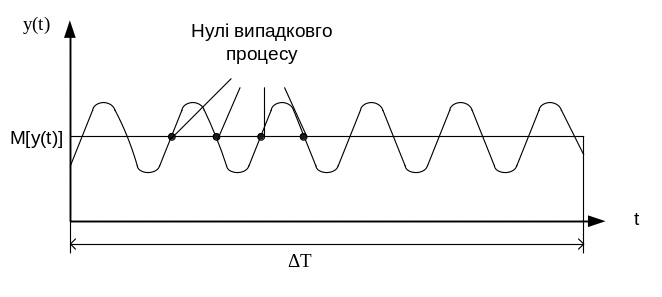[3] [4]

M[y(t)] математична модель сподівання значень сигналу

ΔТ – тривалість реалізації випадкового процесу

Нулі випадкового процесу – це точки перетину кривої цього процесу і лінії математичного сподівання .

Доведемо, що період квантування в часі t₀ може бути визначений за параметрами випадкового процесу таким чином:

D_e – дисперсія завади

D – Дисперсія випадкового процесу (сигналу) авто кореляційної функції процесу

Δmin=ΔT/N₀

N₀ – число нулів випадкового процесу на інтервалі ΔT

У зв’язку з тим, що на сьогодні виготовляються багато АЦП із малим періодом квантування в часі t₀ наведені вище способи можуть бути застосовані для перевірки правильності вибору t₀ для особливо швидкоплинних процесів

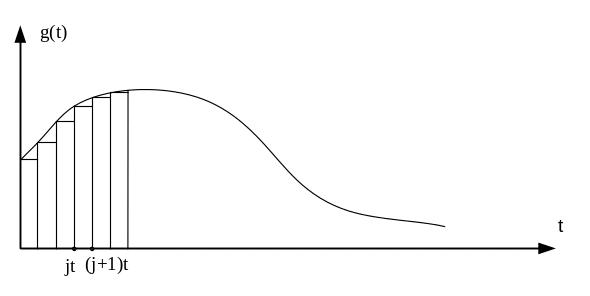
3. Визначення проміжних значень параметру на інтервалі t₀

Метод екстраполяції нульового порядку полягає в тому , що значення сигналу приймається рівним значенню його попереднього відліку на всьому проміжку часу t₀

g(t) = g(jt₀), для jt₀≤t<(j+1)t₀

[5]