Сложный трубопровод.

Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением и/или с разветвлениями.

Пример 4. Вода перетекает из сосуда А в сосуд В под напором Н по сложному трубопроводу, состоящему из четырёх простых трубопроводов, два из которых (2 и 3) соединены параллельно. Для наглядности на входе и выходе участков трубопроводов установлены пьезометры. Определить расходы и потери напора на каждом участке трубопровода, если известны геометрические размеры и величина напора Н.

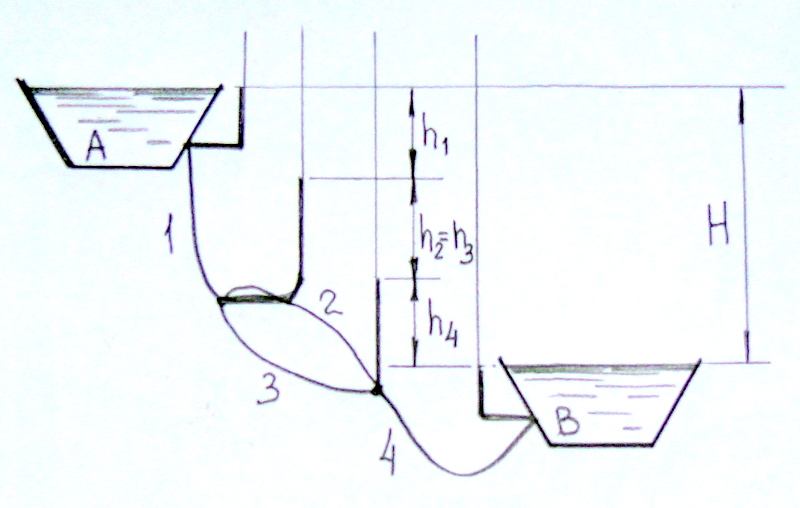
Дано:

м ;

м ; м ;

м ; м ;

м ; м ;

м ; м ;

Решение:

Составим систему 6 алгебраических уравнений с 6 неизвестными:

(система 6 уравнений)

А у меня 8 неизвестных и восемь уравнений. Я считаю по-простому: у меня 4 участка и на каждом ищу две величины: расход и потерю напора.

(21)

Решите эту систему одним из Ваших любимых методов и сравните Ваши результаты с моими ответами:

Ответы: м³/ч; м³/ч; м³/ч; м³/ч;

м ; м ; м ; м

Кольцевой трубопровод.

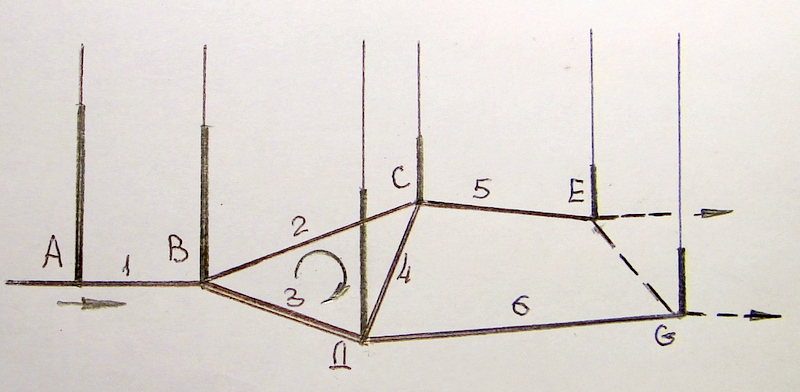
Сложный кольцевой трубопровод в общем случае составлен из смежных замкнутых контуров, с отбором жидкости в узловых точках. В качестве примера на рисунке показан фрагмент сложного кольцевого трубопровода, состоящего из 6 участков простых трубопроводов. Методика гидравлического расчёта кольцевого трубопровода основана на применении двух очевидных правил:

1. алгебраическая сумма расходов в каждом узле равна нулю (вспомните первый закон Кирхгофа);

2. алгебраическая сумма потерь напора на каждом замкнутом контуре при обходе его в одном направлении, например, по часовой стрелке, равна нулю (вспомните второй закон Кирхгофа).

Пример 5. Для фрагмента кольцевого трубопровода, состоящего из «длинных» простых трубопроводов 1 – 6 и узлов В, С и Д известны статические напоры в точках А, Е и G, а также все геометрические размеры. Требуется найти расходы, статические напоры в узлах и потери напора для каждого участка, всего 15 величин.

Дано: м ; м ; м

№	d, м	l,м
1	0,05	100	0,025
2	0,05	60	0,025
3	0,02	50	0,022
4	0,032	20	0,023
5	0,032	120	0,023
6	0,05	160	0,025

Решение. Составим систему 15 алгебраических уравнений с 15 неизвестными:

(22)

Решите эту систему одним из Ваших любимых методов и сравните Ваши результаты с моими ответами (я решал эту систему уравнений с помощью стандартной программы Mathcad14):

Ответы:

м³/ч; м³/ч; м³/ч; м³/ч; м³/ч; м³/ч;

м; м; м;

м ; м ; м ; м ; м ; м

3. Метод эквивалентных замен

Сущность метода эквивалентных замен заключается в том, чтобы свести задачу гидравлического расчёта сложного трубопровода к решению задачи гидравлического расчёта простого «длинного» трубопровода постоянного сечения.

Эквивалентная замена последовательного соединения трубопроводов.

Две трубы называют эквивалентными, если они при одинаковом расходе имеют одинаковые потери напора. Пусть имеем последовательное соединение двух участков трубопровода с разной геометрией.

Трубопровод 1:

Трубопровод 2:

Поставим задачу заменить трубопровод 2 эквивалентным трубопроводом с диаметром , коэффициентом сопротивления трения и скоростью . Поскольку расход при последовательном соединении трубопроводов одинаков для каждого участка, задача сводится к отысканию эквивалентной длины :

Потери напора в первом трубопроводе

Потери напора во втором трубопроводе

Потери напора в эквивалентном трубопроводе (23)

По определению , а расходы в трубопроводах при их последовательном соединении равны:

или , (24)

Эквивалентную длину трубопровода 2 найдём из формулы (23):

(25)

Зная эквивалентную длину второго трубопровода, мы можем заменить расчётную схему последовательного соединения двух трубопроводов на расчётную схему одного простого трубопровода с параметрами:

и . Полные потери напора на последовательном соединении двух трубопроводов можно подсчитать по формуле:

, где (26)

Эквивалентная замена местного сопротивления.

Допустим, что мы имеем на трубопроводе с параметрами местное сопротивление с параметрами: .

Участок трубопровода называют эквивалентным местному сопротивлению, если при одинаковых расходах они имеют одинаковые потери напора.

Поставим задачу заменить местное сопротивление эквивалентным участком трубопровода с диаметром , коэффициентом сопротивления трения и скоростью . Задача сводится к отысканию эквивалентной длины :

Потери напора на местном сопротивлении

Потери напора в эквивалентном трубопроводе (27)

По определению , а расходы в трубопроводе и через местное сопротивление одинаковы:

или или (28)

Эквивалентную длину трубопровода найдём из формулы (27):

(29)

В случае равенства диаметров уравнение (29) упрощается:

(30)

Зная длину трубопровода, эквивалентную местному сопротивлению, мы можем заменить расчётную схему трубопровода с местным сопротивлением на расчётную схему одного простого трубопровода без местных сопротивлений с параметрами: и . Полные потери напора можно подсчитать по формуле:

, (31)

где L - приведенная длина трубопровода.

Эквивалентная замена параллельного соединения трубопроводов.

Допустим, мы рассчитываем параллельное соединение двух трубопроводов:

Трубопровод 1:

Трубопровод 2:

Поставим задачу заменить параллельное соединение двух трубопроводов одним эквивалентным трубопроводом с диаметром , коэффициентом сопротивления трения и расходом, равным сумме расходов через параллельные участки трубопроводов. Найдём эквивалентную длину .

Потери напора в первом трубопроводе

Потери напора во втором трубопроводе

Потери напора в эквивалентном трубопроводе (32)

По определению , а расходы в трубопроводах при их параллельном соединении суммируются: .

(33)

Эквивалентную длину параллельного соединения найдём из формулы (33):

(34)

Обобщая на случай эквивалентной замены нескольких параллельных участков, получаем:

(35)

Для случая замены n одинаковых параллельных труб получаем:

(36)

Применение метода эквивалентных замен упрощает процедуру гидравлического расчёта сложного трубопровода, так как отпадает необходимость решения системы алгебраических уравнений со многими неизвестными.

При использовании метода эквивалентных замен последовательно вычисляют эквивалентные длины местных сопротивлений, последовательных и параллельных участков трубопроводов, получая в конечном счёте параметры простого трубопровода, эквивалентного по гидравлическим характеристикам исходному сложному трубопроводу.

Цунами обрушилось 26.10.2010 на западное побережье Индонезии на следующий день после землетрясения магнитудой 7,5 баллов, которое произошло 25.10.2010 под океанским дном в месте геологического разлома. В этом же месте ровно 4 года назад случилось землетрясение магнитудой 9 баллов. От Цунами в 2004 г. погибло 226 000 человек.