2. Аналитический метод расчета трубопроводов и воздуховодов

Мы рассмотрим три метода расчёта трубопроводов:

Аналитический, графоаналитический метод и метод эквивалентных замен.

Последний из указанных методов представляет собой скорее расчётный приём и дополняет первые два метода. В последние годы этот расчётный приём стал интенсивно использоваться в технологии продаж систем кондиционирования. Настолько широко, что в технической документации стали помещать таблицы эквивалентных длин местных сопротивлений (колена, тройники, рефнеты, коллекторы, сварные соединения, переходы с одного диаметра на другой). Поэтому мы познакомимся и с методом эквивалентных замен..

Методы расчёта водопроводов и воздуховодов систем вентиляции совпадают, гидравлические расчёты систем отопления, водоснабжения, вентиляции и кондиционирования воздуха ничем не отличаются друг от друга ни расчётными формулами, ни последовательностью расчётов. Совпадают также термины и определения.

Методы гидравлических расчётов настолько отработаны, что они включены в строительные нормативы, в Строительные нормы и правила, например, в СНиП 2.04.02-84. Приложение 10 (обязательное). Гидравлический расчёт трубопроводов. Существуют также вычислительные программы различной сложности и достоверности.

Мы же рассмотрим теоретические основы гидравлического расчёта, общие для всех методов и программ.

Общий подход к расчёту трубопровода заключается в применении уравнения Бернулли и закона сохранения массы. Если трубопровод имеет точки ветвления, то достаточно составить уравнения Бернулли для каждого участка трубопровода между точками ветвления и уравнения баланса расходов для каждой точки ветвления. Общее число уравнений, совпадающее с числом неизвестных, равно сумме числа участков трубопроводов и числа узлов.

Очень полезным и удобным понятием при расчёте трубопроводов является понятие располагаемого напора трубопровода:

Как видно из определения, располагаемый напор равен разности гидростатических напоров в сечениях трубопровода и может быть вычислен, как разность пьезометрических уровней в этих же сечениях.

Простой трубопровод.

Простым трубопроводом называют трубопровод без разветвлений. Простой трубопровод может быть сколь угодно протяжённым, дорогим, разнообразным, иметь многие местные сопротивления (вентили, отводы, соединения) и участки с разными диаметрами труб, быть очень сложным и трудным в изготовлении, но если на всём своём протяжении он не имеет разветвлений или ответвлений, то он – простой. Понятно, что в любых сечениях простого трубопровода расход одинаков, а гидравлические элементы расположены последовательно.

Основными параметрами простого трубопровода являются геометрические размеры каждого его участка, тип и количество местных сопротивлений, расход, потери напора. В зависимости от задач, которые стоят перед инженером, всегда известна часть параметров, например, из технического задания на проектирование, или из актов обследования. Остальные величины предстоит найти расчётом.

Типичной целью гидравлического расчёта простого трубопровода является определение расхода при заданных напоре и геометрии.

Жизнь может ставить и обратные задачи: например, каким должен быть диаметр трубопровода, чтобы при располагаемом напоре расход соответствовал бы требуемому значению.

Перейдём в формуле Дарси-Вейсбаха от средней скорости потока к расходу:

или

(6)

Выполнив аналогичные преобразования в формуле Дарси, получим:

или

(7)

Потери напора на отдельных участках простого трубопровода суммируются: общая потеря напора равна сумме потерь напора на всех местных сопротивлениях и потерь напора по длине каждого участка трубопровода:

(8)

«Длинным» трубопроводом называют простой трубопровод, в котором скоростной напор пренебрежимо мал по сравнению с общей потерей напора по длине трубопровода. Если даиметр трубопровода постоянен по всей его длине, то:

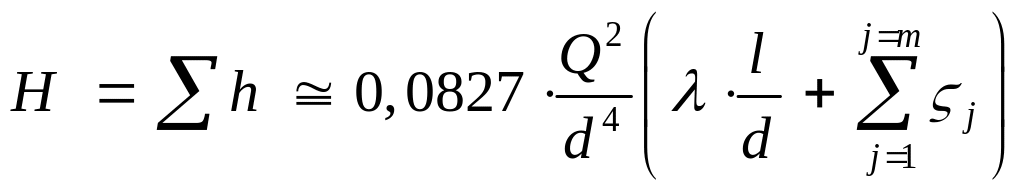(9)

Пример 1. Из сосуда А в сосуд В по простому трубопроводу перетекает вода. Найти расход.

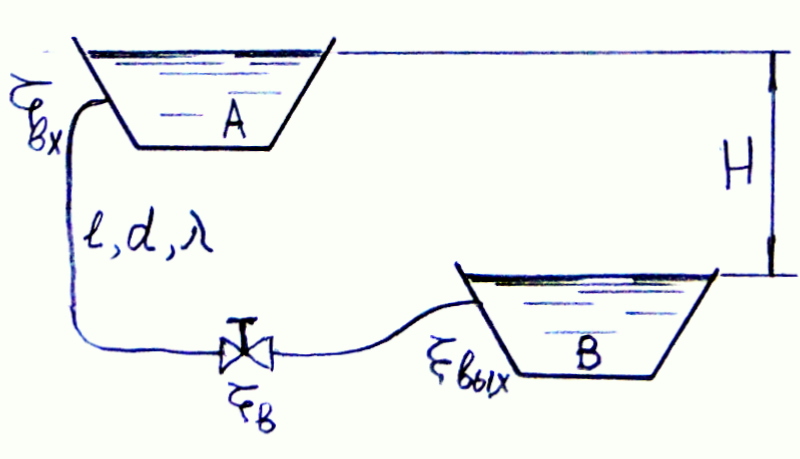
м;

м; м; ;

Решение.

Применим уравнение (9), приравнивая располагаемый напор суммарным гидравлическим потерям

(10)

Или

(11)

Ответ: м³/с ; ( м³/ч )

Заметим, что сумма трёх коэффициентов местных потерь в этом примере равна 6,5 , а слагаемое . Такой трубопровод можно было бы считать «длинным», а приближённый ответ был бы равен м³/с (различие ответов менее 1%).

Последовательное соединение простых трубопроводов представляет собой тоже простой трубопровод и суммарные потери напора можно рассчитать по формуле (9), руководствуясь правилами:

- общая потеря напора равна сумме потерь на каждом участке и на каждом местном сопротивлении;

- расходы в каждом участке трубопровода равны между собой.

Параллельное соединение простых трубопроводов. Участки простого трубопровода можно считать параллельными, если они имеют общие точки входа и выхода и работают под одной разностью напоров. Параллельное соединение простых трубопроводов следует рассчитать, руководствуясь правилами:

- потери напора на каждом из параллельных участков трубопровода равны между собой;

- общий расход через параллельное соединение трубопроводов равен сумме расходов через все параллельные участки.

Пример 2. Участок трубопровода А-В состоит из двух параллельных труб. Определить, как распределится по этим трубам расход , и найти потери напора на участке А-В. Разностью геометрических напоров в точках А и В пренебречь

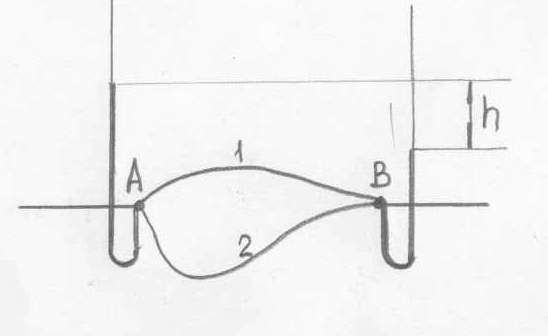
м³/ч

м; м;

м; м;

Решение.

Составим систему 4 алгебраических уравнений с 4 неизвестными величинами :

(12)

Нетрудно видеть, что первое уравнение можно преобразовать следующим образом:

(13)

Или:

(14)

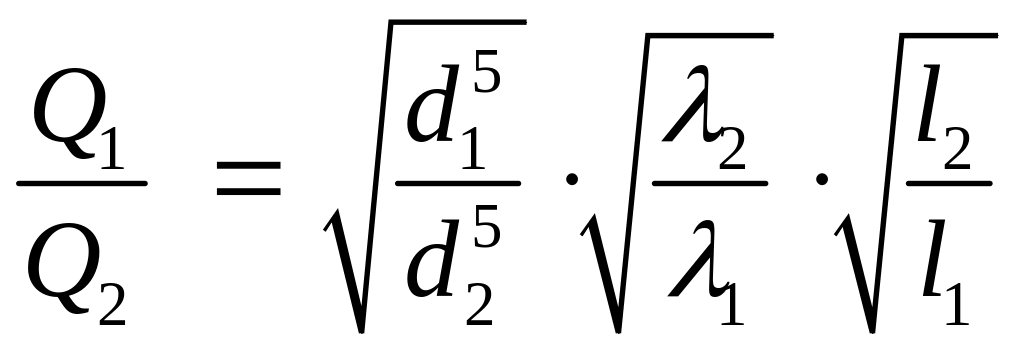(15)

Пожалуйста, проверьте ответы: м³/ч; м³/ч; м

Обратите внимание, что по трубе, диаметр которой в два раза меньше диаметра параллельной трубы, расход почти в 6 раз меньше!

Разветвленное соединение простых трубопроводов.

Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение - место разветвления (или смыкания) труб.

Пример 3. Трубопровод 3 имеет разветвление на два простых трубопровода 1 и 2.

Определить расходы в трубопроводах 1 и 2, а также давление в точке А, если известен расход в трубопроводе 3 и геометрия трубопроводов.

м³/ч ;

м; м; м;

м; м;

м; м;

Решение.

Составим систему алгебраических уравнений

Для сечений А и В трубопровода 1 уравнение Бернулли:

(16)

В этом уравнении ; кроме того, обозначим через статический напор в точке разветвления А, который при любом расходе остаётся одинаковым для входных сечений в оба участка трубопровода 1 и 2. Из уравнения (16) следует:

(17)

Аналогично, для трубопровода 2 ( ):

(18)

(20)

Отметим, что в силу уравнений (17) и (18) потери на трение на участке 2 численно равны статическому напору в точке А : , а потери на трение на участке 1 равны .

Решим систему уравнений (17-20) одним из известных способов. Пожалуйста, проверьте ответы:

м³/ч ; м³/ч ; м ; м ; кПа