Лекция № 7. Обтекание тел потоком идеальной несжимаемой жидкости.

План лекции.

1. Потенциал скорости и функция тока. Комплексный потенциал.

2. Метод конформных отображений. Преобразование Н.Е.Жуковского.

3. Обтекание тел (круга, эллипса, крыловых профилей)

4. Ползущие течения, лоток Хил Шоу

1. Потенциал скорости и функция тока. Комплексный потенциал.

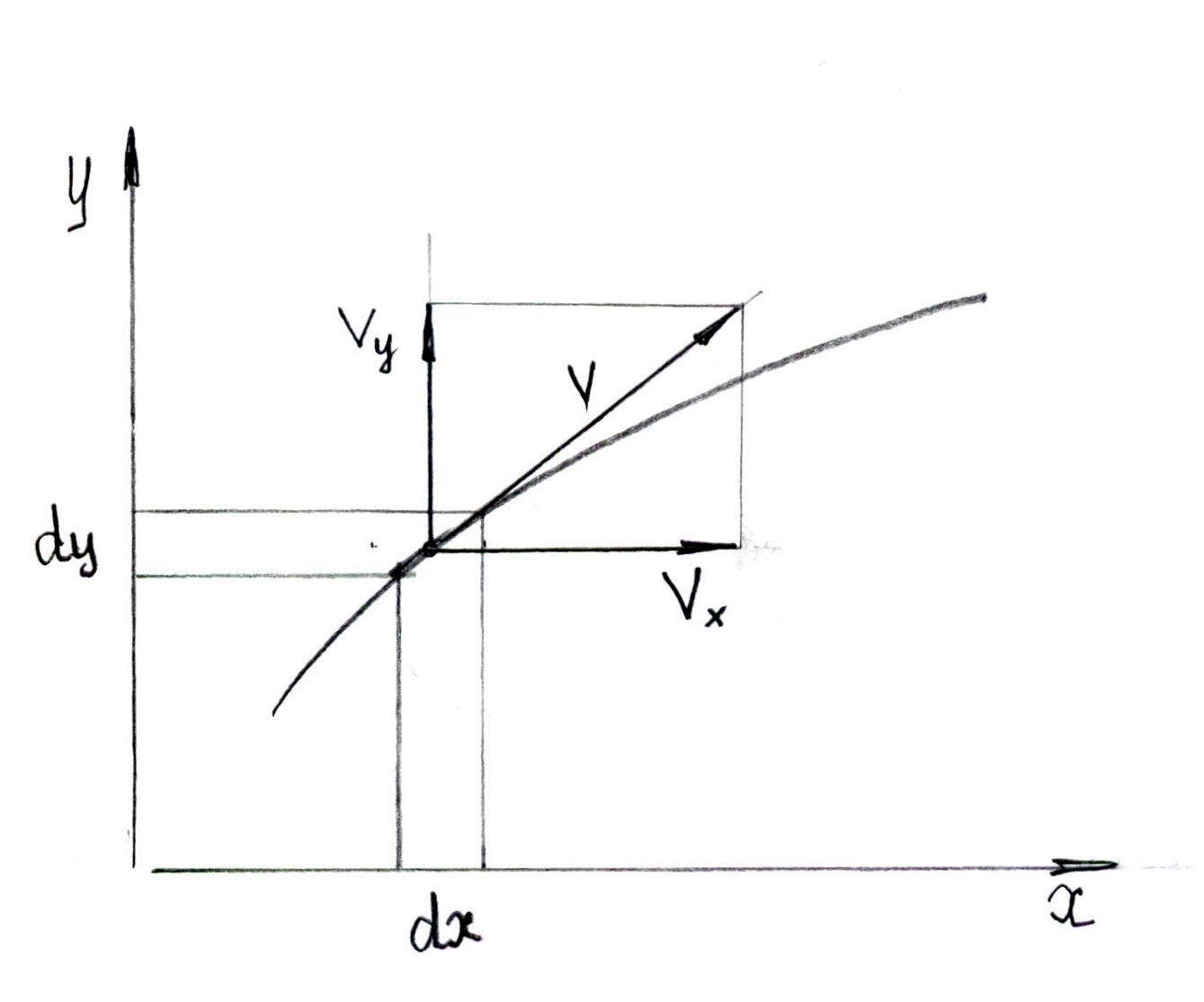
При установившемся движении жидкости линии тока совпадают с траекториями. Дифференциальное уравнение траектории можно получить, выразив тангенса угла наклона касательной к траектории двумя разными способами (вектор скорости направлен по касательной к линии тока):

(1)

Или

(2)

Известно, что для того, чтобы выражение являлось полным дифференциалом функции , необходимо и достаточно выполнение условия:

(3)

Следовательно, левая часть выражения (2) является полным дифференциалом функции лишь в том случае, когда выполнены условия:

(4)

Условие (4) всегда выполняется для движения несжимаемой жидкости, так как оно является уравнением неразрывности, и, следовательно, функция , называемая функцией тока, всегда существует.

Полный дифференциал функции тока можно записать двумя способами:

(5)

(6)

Сопоставляя выражения (5) и (6), получим:

(7)

Семейство траекторий в конкретном поле скоростей имеет вид:

(8)

Физический смысл функции тока

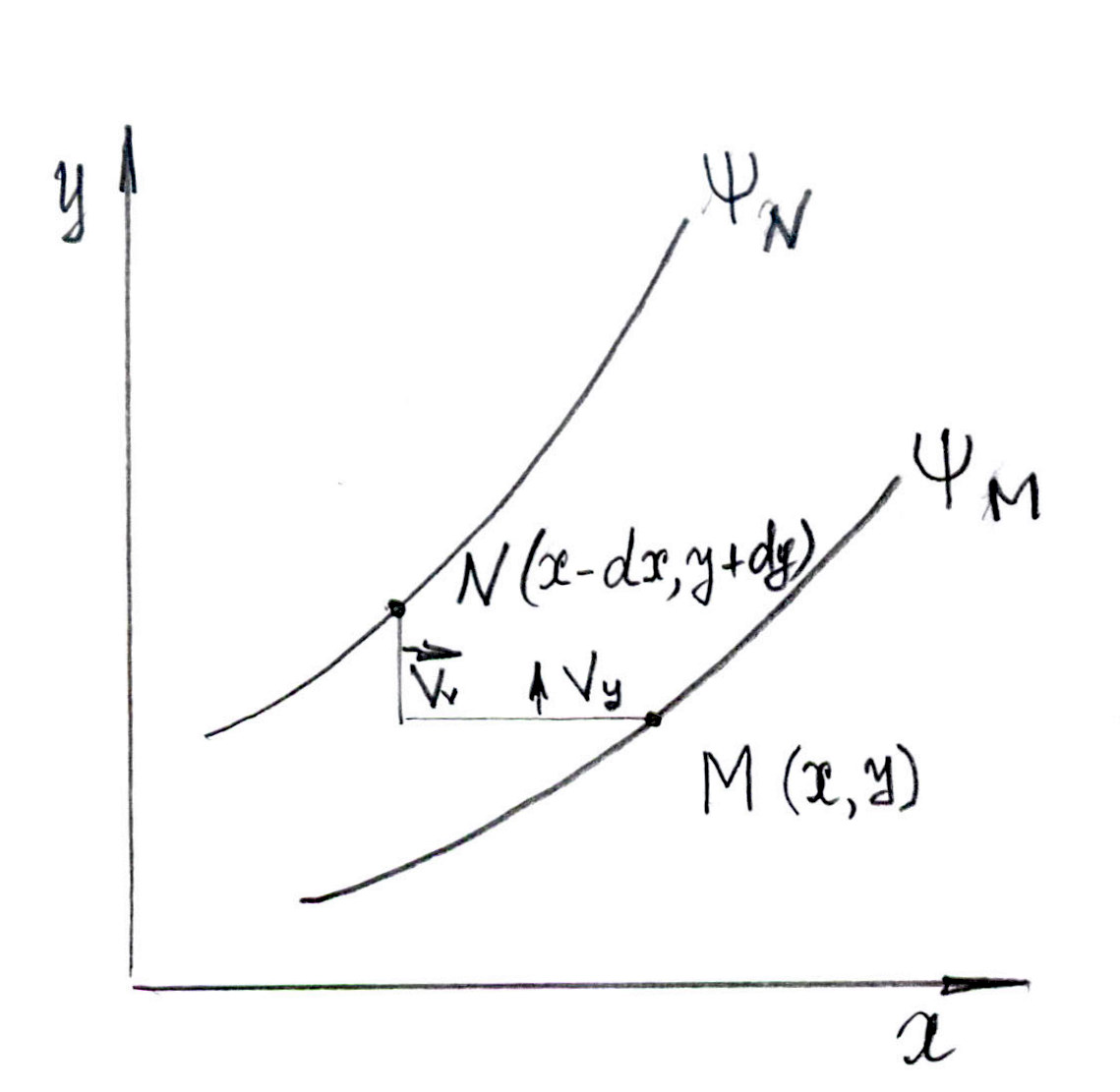
Рассмотрим плоское движение жидкости в координатах x – y (ось z направлена перпендикулярно плоскости рисунка). Выделим внутри потока две близкие траектории, проходящие через точки М и N.

(9)

Эти траектории можно рассматривать как проекции на плоскость x – y двух вертикальных поверхностей тока, параллельных оси z, и проходящих через эти точки. Расход жидкости между поверхностями тока не изменяется по величине (вектор скорости в любой точке поверхности тока направлен по касательной к ней) и, следовательно, поперечная составляющая скорости на поверхности тока равна нулю – поверхность тока непроницаема для жидкости.

Расход жидкости через площадку, ограниченную поверхностями тока, походящими через точки М и N, и сечениями, параллельными плоскости х0у и отстоящими друг от друга на единицу длины 1 м, можно подсчитать следующим образом:

(10)

или, используя (7):

(11)

Это означает, что расход жидкости, протекающей между поверхностями тока, может быть вычислен как разность значений функции тока, соответствующих этим поверхностям:

(12)

Следовательно, физический смысл функции тока заключается в том, что она равна объёмному расходу жидкости между данной поверхностью тока и той поверхностью тока, для которой функция тока принята равной 0.

Потенциал скорости.

Плоское (двухмерное) течение называется потенциальным, если в исследуемой области течения существует скалярная функция двух переменных , для которой выполняются соотношения:

(13)

Функцию называют потенциалом поля скоростей (потенциалом скоростей).

Потенциал скоростей является однозначной функцией координат и определяется с точностью до постоянной. Изопотенциальные линии и линии тока в любой точке плоскости течения взаимно ортогональны. Потенциальное поле скоростей является безвихревым (докажите это самостоятельно).

Из соотношений (7) и (13) следует выполнение условий Коши-Римана:

(14)

в силу которых комплексная функция

(15)

является не просто и не только функцией двух переменных (координат ) , но и функцией одной комплексной переменной z :

(16)

Комплексную функцию называют комплексным потенциалом. Плоскость 0xy значений комплексной переменной z называют физической плоскостью или плоскостью течения.

Важным свойством комплексного потенциала является следующее: производная комплексного потенциала по комплексному аргументу равна сопряжённой скорости:

. (17)

В частности, это означает, что если известен комплексный потенциал , то найти проекции скорости на оси координат можно по формулам:

(18)