Підготовка до роботи
1.
Визначити свій варіант системи
перемикальних функцій (табл.. 3. 4). Для
цього необхідно одержати вісім молодших
розрядів номера залікової книжки
студента, поданого в двійковій системі
числення (
),
а потім підставити
в табл. 3. 4 і в табл. 3. 5.
2. Виконати спільну мінімізацію функцій та їх заперечень методом Квайна або Квайна – Мак-Класкі.
3. Одержати операторні подання функцій для їх реалізації у заданому елементному базисі (див. табл. 3. 5).
4. Побудувати комбінаційні схеми. Що відповідають отриманим операторним формам.
5. Визначити та порівняти параметри одержаних схем.
Таблиця 3. 4
-
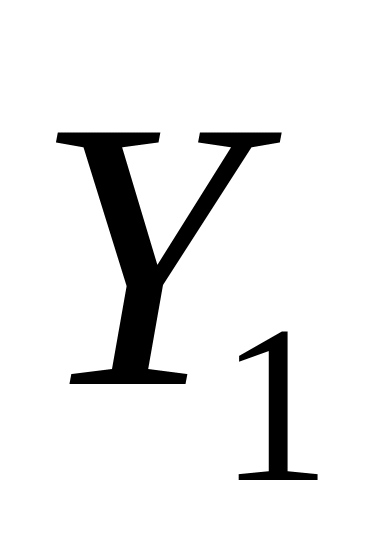
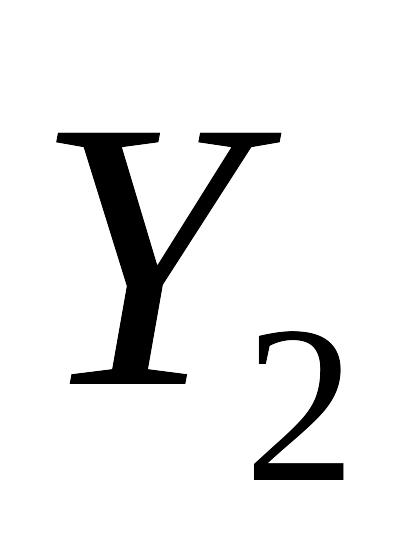
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
0
0
0
1
1
1
1
0
1
0
0
0
1
0
1
0
1
0
1
1
0
1
1
0
1
1
1
0
1
1
0
0
0
1
0
0
1
1
0
1
0
0
0
1
0
1
1
1
1
0
0
1
1
0
1
1
0
1
1
1
0
1
1
1
1
Порядок виконання роботи
1. Побудувати моделі комбінаційних схем за допомогою програмного комплексу ПРОГМОЛС 2.0
2. Переконатися в правильності функціонування моделей.
3. Визначити часові параметри комбінаційних схем за допомогою часових діаграм, порівняти їх з одержаними теоретично.
Таблиця 3. 5
|
|
|
Тип елементів |
Число елементів в корпусі |
Час затримки сигналу, нс. |
0
|
0 |
0 |
3 І – НЕ 3 І |
3 3 |
10 14 |
0 |
0 |
1 |
4 ! – НЕ 2 АБО |
2 4 |
10 12 |
0 |
1 |
0 |
4 І 2 АБО - НЕ |
2 4 |
14 12 |
0 |
1 |
1 |
3 І – НЕ 2 АБО |
3 4 |
10 12 |
1 |
0 |
0 |
2 АБО – НЕ 3 І |
4 3 |
12 14 |
1 |
0 |
1 |
2 АБО – НЕ 4 І |
4 2 |
12 14 |
1 |
1 |
0 |
2 І – НЕ 3 АБО |
4 3 |
12 12 |
1 |
1 |
1 |
3 АБО – НЕ 4 АБО |
3 2 |
12 12 |