Комп’ютерна логіка методичні вказівки до лабраторних робіт

КИЇВ – 2012

Кожній лабораторній роботі передує самостійна підготовка студентів, у процесі якої вони докладно вивчають опис лабораторної роботи, відповідні розділи посібника й додаткові літературні джерела, Розділи посібника для підготовки до роботи вказані в заголовках робіт. Додаткова література наведена в кінці опису кожної роботи.

У процесі підготовки складається звіт про лабораторну роботу, в якому відображаються всі пункти завдання, а також заготовлені необхідні для експериментальної частини лабораторної роботи таблиці, осі часових діаграм, комбінаційні схеми тощо.

Перед виконанням лабораторної роботи результати підготовки перевіряються викладачем. Студент має сформувати мету і порядок виконання лабораторної роботи, представити підготовлений звіт і відповісти на контрольні питання. Непідготовлений студент до виконання лабораторної роботи не допускається.

Перед виконанням наступної лабораторної роботи студент повинен представити цілком оформлений звіт за попередню роботу. Звіт має містити короткі теоретичні відомості, необхідні для виконання завдання, відповіді на контрольні питання, Усі схеми, формули, таблиці, діаграми, графіки, отримані під час виконання завдання та в процесі експериментального дослідження схем, а також висновки по роботі. Студент, який не представив звіт, не допускається до виконання наступної лабораторної роботи. Оцінку за виконання лабораторної роботи студент одержує після співбесіди з викладачем за темою лабораторної роботи.

Для проведення лабораторних робіт використовується програмний комплекс моделювання цифрових схем ПРОГМОЛС 2.0(див. додаток 1).

Лабораторна робота 1 Проектування комбінаційних схем

Мета роботи: оволодіти методами побудови комбінаційних схем у заданому елементному базисі, визначення складності і дослідження швидкодії комбінаційних схем.

Короткі теоретичні відомості

Перемикальною або логічною функцією називається функція, що сама функція і кожен з її аргументів приймають значення тільки із множини {0, 1}.

Перемикальна функція може бути задана різними способами: словесним описом; матричним способом (таблицею істинності); геометричним представленням; аналітичним виразом.

Наприклад, словесно перемикальну функцію можна описати так: функція від аргументів і приймає значення одиниці, якщо більшість її аргументів приймає нульові значення.

Задану вище перемикальну функцію можна зобразити у вигляді таблиці істинності (табл. 1.1), де надано всі можливі двійкові набори та значення функції на цих наборах.

Таблиця 1.1

Таблиця істинності

Номери наборів	Набори аргументів			Значення функції
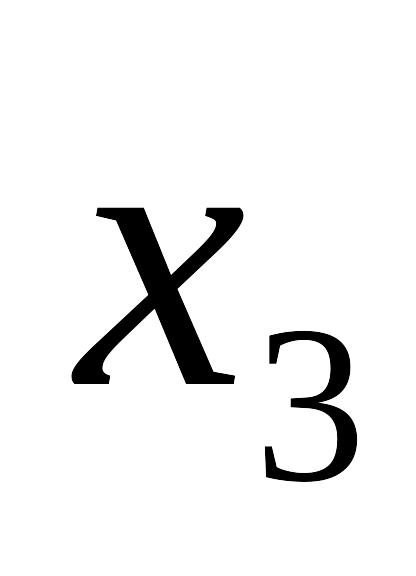
0	0	0	0	1
1	0	0	1	1
2	0	1	0	1
3	0	1	1	0
4	1	0	0	1
5	1	0	1	0
6	1	1	0	0
7	1	1	1	0

Набором називають упорядковану послідовність значень аргументів перемикальної функції.

Двійковий набір має довжину n, якщо він представлений n цифрами із множини {0, 1}. В табл. 1. 1 перелічені всі двійкові набори. Очевидно, що набір значень аргументів фактично є деяким двійковим числом. Між

двійковими наборами і двійковими числами існує взаємно однозначна відповідність. Отже, існує 2ⁿ різноманітних наборів двійкових змінних.

Кожний набір має свій номер, який збігається з кількісним еквівалентом двійкового числа. Наприклад, якщо набори впорядковуються у послідовності … , то номер набору визначається як

Отже, двійкові набори в таблиці істинності перемикальної функції можуть бути надані їх номерами.

Табличний спосіб подання перемикальної функції є наглядним і теоретично може бути застосований для запису функцій довільної кількості змінних. Для визначення функції не обов’язково задавати її значення на всіх наборах. Достатньо визначити всі набори, які перетворюють цю функцію в нуль, чи всі набори, що перетворюють її в одиницю.

Недоліком табличного способу подання перемикальних функцій є його громіздкість, яка зростає із збільшенням аргументів функції. Так, наприклад, таблиця істинності перемикальної функції 10 змінних буде містити 2¹⁰ = 1024 рядків.

При геометричному представленні функцію від аргументів можна задати -мірним кубом. Наприклад, геометричне зображення перемикальної функції трьох аргументів, заданої у табл. 1.1, наведене на рис. 1.1,в. Кількість вершин дорівнює кількості наборів. Точкою позначені набори, на яких функція має одиничне значення.

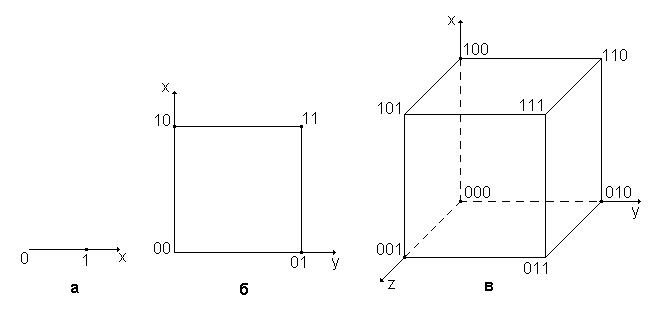
Рис. 1. 1. Геометричне зображення перемикальних функцій:

а – однієї змінної; б – двох змінних; в – трьох змінних

Геометричне подання перемикальної функції, як і табличне, також значно ускладнюється за збільшення кількості аргументів функції. Тому значно простіше виглядає аналітичний запис у вигляді формул.

При аналітичному способі перемикальна функція задається формулами, тобто аналітичними виразами, побудованими за допомогою логічних операцій різних алгебр перемикальних функцій, наприклад:

;

Логічний елемент – це електронна схема, що реалізує певну перемикальну функцію. На функціональних схемах логічний елемент зображається за допомогою умовного графічного позначення.

На практиці використовують порівняно невеликий набір перемикальних функцій для побудови інших , більш складних функцій за допомогою методу суперпозиції функцій.

Під суперпозицією функцій розуміють підстановку замість аргументів однієї функції значень інших функцій.

Суперпозиції функцій відповідає певна логічна схема. Логічною схемою називають сукупність взаємозв’язаних логічних елементів.

Існують два різновиди логічних схем: комбінаційні і послідовнісні.

Комбінаційна схема – це така схема, функціонування якої може бути описане системою перемикальних функцій:

;

;

…………………

,

де − кількість входів; − кількість виходів схеми.

Комбінаційна схема має тільки один стан. Тому вихідні сигнали комбінаційної схеми залежать тільки від значень вхідних логічних сигналів. Основною ознакою комбінаційних схем є відсутність петель.

Петля – це шлях від виходу логічного елемента до його входу, можливо, через інші логічні елементи.

Послідовнісні схеми мають більше ніж один стан. Тому в них вихідні сигнали залежать не тільки від вхідних сигналів, а й від стану, в якому перебуває схема. Основною ознакою послідовнісних схем є наявність петель.

Як комбінаційні, так і послідовнісні схеми називають цифровими автоматами. При цьому комбінаційні схеми мають назву тривіальних автоматів, або автоматів без пам’яті а послідовнісні схеми називають автоматами з пам’яттю.

Логічні схеми найчастіше характеризують складністю схеми (структурний параметр) та затримкою сигналів схемою (часовий параметр).

Існує декілька способів оцінки складності логічних схем. Розглянемо найбільш уживані з них.

Оцінка складності логічних схем за Квайном полягає у знаходженні суми входів логічних елементів комбінаційної схеми:

,

де − кількість елементів; − кількість входів -го елемента.

Отже, для визначення складності К знайти сумарну кількість входів усіх логічних елементів схеми.

Складність логічної схеми можна також оцінити числом умовних корпусів мікросхем логічних елементів, що визначається за виразом

,

Де − кількість типів елементів; − кількість елементів -го типу;

− кількість виводів (входів і виходів) елементів -го типу;

− число виводів умовного корпусу мікросхеми логічних елементів.

Параметри складності і використовуються під час проектування інтегральних схем (як порівняльна оцінка складності варіантів проектування).

Швидкодія логічних схем залежить від затримки сигналів логічними елементами, яка визначається часовими логічних елементів (перемикання з 0 в 1) і (перемикання із 1 в 0).

Під затримкою сигналів елементом розуміють час переходу вихідного сигналу елемента від одного логічного рівня до іншого від моменту зміни значення вхідних сигналів, що викликають цей перехід. На практиці використовують усереднене значення затримки сигналів або максимальне .

Для комбінаційних схем, побудованих на однотипних елементах, середній час затримки сигналів дорівнює

,

де − кількість логічних елементів, що входять в максимальний за

довжиною ланцюжок елементів логічної схеми;

− затримка сигналу логічним елементом.

Якщо використовуються елементи з різною затримкою, то в схемі визначається шлях, який вимагає максимального часу поширення сигналів від входів до виходу.

Мінімальний період зміни вхідних сигналів визначається з урахуванням максимальної затримки сигналів у схемі. Він не може бути меншим максимальної затримки сигналів. Виходячи з цього визначається і максимальна частота зміни наборів вхідних сигналів.

На практиці під час побудови логічних схем можуть використовуватися логічні елементи, що реалізують функції різних алгебр. Найчастіше елементний базис, обумовлений мікроелектронною технологією, містить елементи з множини {І, АБО, НЕ, І-НЕ, АБО-НЕ}, тобто складається з елементів алгебр Буля, Шефера і Пірса. Таку систему функцій можна розглядати в аспекті розширеної практичної алгебри, яка має сукупні властивості відповідних алгебр.

Розширена алгебра має вісім нормальних форм представлення перемикальних функцій, котрі забезпечують побудову дворівневих комбінаційних схем, якщо на кількість входів логічних елементів немає обмежень.

Чотири нормальні форми поширеної алгебри можна одержати виходячи із ДДНФ і ще чотири – виходячи із ДКНФ перемикальної функції або ДДНФ заперечення функції. Якщо немає обмежень на кількість входів логічних елементів, то такі форми перемикальних функцій забезпечують побудову дворівневих комбінаційних схем.

Нормальним формам зручно надати назву, що складається із назв внутрішньої та зовнішньої операції. Наприклад ДДНФ може отримати назву форми І / АБО, ДКНФ – АБО / І і таке інше.

Розглянемо нормальні форми поширеної алгебри перемикальної функції двох аргументів , заданої таблицею істинності (табл. )

Таблиця Таблиця істинності

0 0 0 1 1 0 1 1	1 0 0 1

У формі ДДНФ і ДКНФ задана перемикальна функція має відповідно вигляд:

;

.

Виходячи із ДДНФ з урахуванням аксіоми та правила де Моргана (2) одержимо перші чотири нормальні форми:

(І / АБО)

(І-НЕ / І-НЕ)

(АБО / І-НЕ)

. (АБО-НЕ / АБО)

На базі ДКНФ аналогічним чином отримаємо ще чотири нормальні форми:

(АБО / І)

(АБО-НЕ / АБО-НЕ)

((І / АБО-НЕ)

. (І-НЕ / І)

Останні чотири форми можна аналогічно одержати виходячи із заперечення перемикальної функції, що відповідає формі І / АБО-НЕ.

Для отримання заперечення функції виписують із запереченням кон’юнктивні терми наборів, на яких функція дорівнює нулю, поєднані операцією диз’юнкції.

Заперечення даної функції має вигляд:

.

Послідовно отримаємо:

(І / АБО-НЕ)

(І-НЕ / І)

(АБО / І)

. (АБО-НЕ / АБО-НЕ)

Для побудови схеми можуть використовуватися різні форми, які залежать від елементного базису. Наприклад, за наявності елементів І, АБО, І-НЕ можна вибрати одну з п’яти нормальних форм: І / АБО,І-НЕ / І-НЕ, АБО / І-НЕ, І-НЕ / І, АБО / І, якщо задані елементи І-НЕ, АБО-НЕ, то підходять форми І-НЕ / І-НЕ та АБО-НЕ / АБО-НЕ і т. д.

Якщо число входів логічних елементів достатнє для реалізації нормальної форми, то така форма водночас є операторною. У випадку, коли число входів логічних елементів менше, ніж потрібно для реалізації нормальної форми, для одержання операторної форми змінні поєднують у групи, що містять не більше елементів, і використовують співвідношення вигляду:

;

;

;

, де і .

Число груп змінних також не повинно перевищувати . В іншому випадку зазначенні перетворення виконують також стосовно груп змінних. Наведені перетворення дозволяють подати функції в операторній формі з урахуванням числа входів логічних елементів. Комбінаційна схема, отримана за такою операторною формою. Може містити більше двох рівнів.

На третьому етапі треба вибрати одну схему з декількох можливих відповідно із заданими параметрами (зазвичай – за складністю та швидкодією).

Таким чином, з декількох можливих обирають комбінаційну схему, що краще за інші задовольняє заданим параметрам.

Наприклад, за наявності двовходових елементів 2І-НЕ та 2АБО-НЕ (цифри показують кількість входів елемента) розглянуту функцію можна подати в нормальних формах І-НЕ / І-НЕ та АБО-НЕ / АБО-НЕ таким чином:

; (І-НЕ / І-НЕ)

. (АБО-НЕ / АБО-НЕ)

Виходячи з цього отримаємо операторні форми:

;

.

За отриманими операторними формами можна побудувати комбінаційні схеми на елементах 2І-НЕ та 2АБО-НЕ (рис.2.9).

У кожній схемі максимальна затримка сигналів визначається ланцюжком із чотирьох елементів, тобто , де − затримка сигналу одним відповідним елементом. Якщо елементи І-НЕ мають менший час затримки сигналів, ніж елементи АБО-НЕ, то комбінаційна схема на рис. 2.9,а має більшу швидкодію, але вона програє комбінаційній схемі на рис.2.9,б за складністю. Складність за Квайном комбінаційної схеми, побудованої на логічних елементах 2І-НЕ, дорівнює К = 12, а схеми на логічних елементах 2АБО-НЕ – К = 10.