Для побудови надійного інтервалу s обчислимо

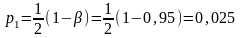
і р₂ = 1 – р₁ = 1 – 0,025 = 0,975.

По таблицям розподілу c² (додаток 4) методом лінійного інтерполювання визначаємо при п -1 = 9 і р₁ = 0,025 та р₂ = 0,975

;

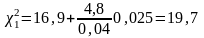За формулою (4.66) отримаємо

; .

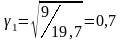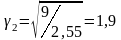По формулі (4.65) обчислюємо

або .

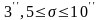Відповідно

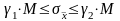або

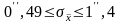
Питання для самоперевірки

1. Які задачі вирішує математична статистика?

2. Що таке генеральна сукупність та вибірка?

3. Що називають статистичною функцією розподілу?

4. Що таке ступінчатий графік та гістограма?

5. Як обчислити довжину та граничні значення інтервалів?

6. Запишіть формули числових характеристик статичного розподілу.

7. Як побудувати гістограму, ступінчатий графік і полігон частот?

8. Властивості доброякісних оцінок параметрів розподілу?

9. Якими способами можна оцінити параметри розподілу?

10. Що таке метод максимальної правдоподібності?

11. Назвіть точкові оцінки параметрів розподілу.

12. Що таке довірчі інтервали?

13. Як задати інтервал для математичного сподівання, дисперсії та стандарту?