
- •§ 1. Основні поняття і задачі математичної статистики. Генеральна сукупність та вибірка
- •§ 2. Розподіл статистичних рядів
- •По даним таблиці 4.2 побудуємо: а) полігон частот
- •§ 4.3 Оцінювання параметрів закону розподілу
- •Сутність ммп полягає в тому, що за якісну оцінку параметра а беруть таке значення аргументу, що приводить функцію l до максимуму. Рівняння (4.14) розв’язують при умові
- •При цьому вибирають таке визначення а, яке зводить функцію l до максимуму. Для спрощення функцію правдоподібності заміняють логарифмом, тоді
- •§ 4.4 Числові характеристики статистичного розподілу
- •Для визначення приблизних значень вимірюваної величини та дисперсії при нерівноточних вимірах, виходячи з того, що ¹ , систему рівнянь (4.19) запишемо у вигляді
- •§ 4.5 Оцінка параметрів розподілу за допомогою надійних інтервалів
- •Надійний інтервал для центра розподілу при невідомому s
- •Надійний інтервал для s
- •Для побудови надійного інтервалу s обчислимо
Надійний інтервал для центра розподілу при невідомому s
В практичній діяльності при проведені дослідів нам невідомо як МХ так і s2. Вони оцінюються по малим статистичним рядам (вибіркам). Тоді від випадкової величини переходять до другої випадкової величини t, що є функцією значень х1, х2,...,хп, закон розподілу якої не залежить від невідомих параметрів величини Х, а залежить тільки від кількості дослідів п і від виду закону розподілу випадкової величини Х. Як показано в § 2.7 при нормальному розподілу величин Х випадкова величина t підкоряється закону розподілу Стьюдента з п-1 степенями вільності (додаток 3).
Тоді стандартом математичного сподівання буде середнє квадратичне відхилення середнього арифметичного М (формула 4.57).
Формула (4.58) прийме вигляд
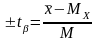 .
(4.61)
.
(4.61)
Надійний інтервал для параметра а = МХ при невідомих і DX знаходиться по формулі
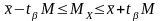 .
(4.62)
.
(4.62)
Згідно розподілу Стьюдента
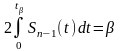 ,
(4.63)
,
(4.63)
де b - ймовірність появи випадкової величини від 0 до tb .
В таблиці розподілу Стьюдента (додаток 3) по надійної ймовірності b і числу ступенів вільності п-1 находять величину tb.
Відповідно з інтервалом (4.61) можна побудувати надійний інтервал для любого значення із вибірки х1, х2,...,хп за формулою

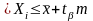 .
(4.64)
.
(4.64)
Надійний інтервал для s
Виходять
з того, що вибірка отримана із нормальної
сукупності. При цьому величина
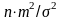 розподілена по закону розподілу c2
(§ 2.6) з (п-1)
ступенями вільності. Слід відмітити,
що для надійної ймовірності b
можна побудувати інтервал нескінченним
числом способів. Проте краще вибрати
такі межі
розподілена по закону розподілу c2
(§ 2.6) з (п-1)
ступенями вільності. Слід відмітити,
що для надійної ймовірності b
можна побудувати інтервал нескінченним
числом способів. Проте краще вибрати
такі межі
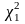 і
і
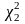 , щоб
, щоб
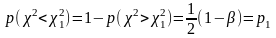 ;
;
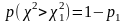 і
і
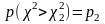 .
.
Тоді
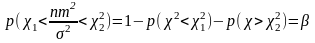 .
(4.65)
.
(4.65)
Це свідчить про те, що
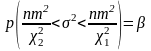 .
(4.66)
.
(4.66)
Таким чином надійний інтервал для s буде
g
1m
 ,
(4.67)
,
(4.67)
де
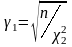 і
і
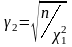 .
(4.68)
.
(4.68)
При невеликій кількості випробувань
 і
і
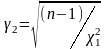 .
(4.69)
.
(4.69)
Величини
і
вибирають
із таблиць розподілу
 (додаток
4) з числом ступенів вільності п
або (п-1)
відповідно для ймовірності
(додаток
4) з числом ступенів вільності п
або (п-1)
відповідно для ймовірності
 і р2
= 1 – р1.
і р2
= 1 – р1.
По аналогії з інтервалом (4.67) можна побудувати надійний інтервал для середнього квадратичного відхилення простої арифметичної середини. Враховуючи формулу (4.57) отримаємо
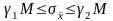 .
(4.70)
.
(4.70)
Приклад. Проведено експериментальні випробування світловіддалеміра на польовому компараторі з довжиною еталонної лінії l = 120,000м. Точність приладу характеризується дисперсією m2 = 5 мм. Випробування проводяться серійно по 10 вимірів в кожному. Визначити інтервали математичного сподівання для кожної вибірки (серії вимірів) та стандартів s і при надійності ймовірності р= 0,95.
Розв’язання. Так як в кожній серії проводиться по п=10 вимірів, то стандарт математичного очікування по формулі (4.56) буде
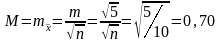 мм.
мм.
По таблицям функції Лапласа (додаток 1) для f = f(t) = 0,95/2 = 0,475 визначаємо t = 2,0. Тоді по формулі (4.59) при = 120,000 м маємо
120,000
– 2,0×
0,0007
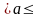 120,000 + 2,0 ×
0,0007, або
120,000 + 2,0 ×
0,0007, або
119,9986 120,0014.
