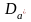Для визначення приблизних значень вимірюваної величини та дисперсії при нерівноточних вимірах, виходячи з того, що ¹ , систему рівнянь (4.19) запишемо у вигляді

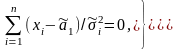. (4.30)

В теорії математичної обробки при нерівноточних вимірах вводять поняття ваги, тобто

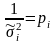, (4.31)

де р_і - вага виміру, або вага випадкової величини х_і. Тоді статистичний ряд (4.29) можна переписати в вигляді

х₁, х₂, ... , х_п,

р₁, р₂, ... , р_п. (4.32)

Вага р_і буде характеризувати міру відносної точності результатів експериментів. При цьому їх можна збільшувати, чи зменшувати на однакове число С. Тоді формула (4.31) буде

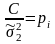. (4.33)

Для спрощення вводять поняття середнього квадратичного відхилення одиниці ваги - 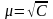. Тоді вага буде обчислюватися за формулою

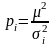, (4.34)

а систему рівнянь (4.30) можна переписати у вигляді

;

.

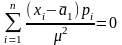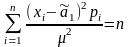Із їх сумісного розв’язання знаходять формули обчислення загальної арифметичної середини 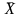і середнього квадратичного відхилення одиниці ваги

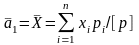; (4.35)

. (4.36)

Очевидно оцінка дисперсії одиниці ваги m² » D_x буде зміщеною. По аналогії з формулою (4.22) незміщеною оцінкою дисперсії одиниці ваги при нерівноточних вимірах буде

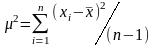. (4.37)

Статистичною оцінкою стандарту або середнього квадратичного відхилення s буде середня квадратична похибка

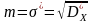. (4.38)

При відомому істинному значенню визначуваної величини а її обчислюють за формулою Гаусса

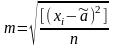. (4.39)

Якщо істинне значення визначуваної величини невідоме, то застосовують формулу Бесселя

, (4.40)

де - середнє арифметичне;

п – число результатів експерименту.

Додатковими статистичними характеристиками нормального закону розподілу є асиметрія та ексцес.

Асиметрія являє собою нормований центральний момент третього порядку, тобто

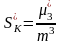. (4.41)

Ексцес є мірою крутизни і визначається по формулі

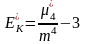, (4.42)

де ; .

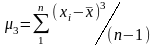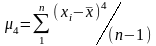Приклад 1. В таблиці 4.3 приведені результати експерименту при дослідженні випадкової величини Х. Визначити числові характеристики статистичного розподілу: 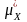, , 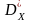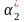і .

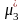Таблиця 4.3

пі	1	2	3	4	5	6	7
хі	-10	-2	+4	-1	+4	+12	+9

Розв’язання. По формулам (4.10) – (4.13) отримаємо

= = (-10 –2 + 4 –1 + 4 + 12 + 9) / 7 = + 2;

= {(-10-2)² + (-2 +2)² + (4 – 2)² + (-1 –2)² + (4 – 2)² + (12 – 2)² + + (9-2)²} / 7 = 310/7 = 44,3;

= {(-10)² + (-2)² + 4² + (-1)² + 4² + 12² + 9² } / 7 = 51,7;

= {(-12)³ + 0³ + 2³ + (-3)³ + 2³ + 10³ + 7³} / 7 = 444,9.

Приклад 2. Із статистичного ряду отримано статистичну сукупність (табл..4.4, рядки 1-7). Обчислити статистичний початковий момент першого порядку та дисперсію другого порядку .

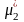Таблиця 4.4

1	№ групи		1	2	3	4	5	6	S
2	Граничні значення	от	-10	-5	0	5	10	15
		до	-5	0	+5	10	15	20
3	Частота nі		2	7	11	14	5	1	40
4	Середні		-7,5	-2.5	+2,5	+7,5	+12,5	+17,5
5	nі		-15	-17,5	+27,5	+105,0	62,5	17,5	180
6	(		-12	-7	-2	+3	+8	+13
7	nі ( 2		288	343	44	126	320	169	1290

Розв’язання. В рядку 5 визначають загальне середнє статичне. Якщо 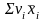= 180, то за формулою (4.14) обчислюємо:

= .

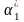Потім обчислюють відхилення середніх групи від загального середнього статистичного . = 4.5. В рядку 7 обчислюють 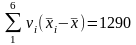. Тоді статистична дисперсія буде дорівнювати .

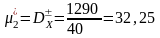Для системи двох випадкових величин (х,у)

Числові характеристики визначають за результатами п-незалежних дослідів, які виконують в однакових умовах по значенням:

Х ® х₁, х₂, ..., х_п;

Y ® y₁, y₂, … , y_n.

В свою чергу системи випадкових величин (х_і, у_і) незалежні, а математичні сподівання, дисперсії і кореляційні моменти будуть однакові, тобто

.

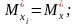
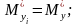
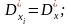
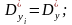
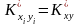Виходячи з того, що випадкові величини х і у та система (Х,Y) підкоряються нормальному закону розподілу, а математичні очікування 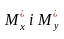та дисперсії 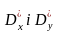є характеристиками окремих випадкових величин Х і Y із системи (Х, Y), то згідно формул (4.20) і (4.22) маємо

; (4.43)

; (4.44)

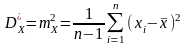; (4.45)

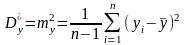(4.46)

Незміщена та обґрунтована оцінка кореляційного моменту 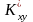системи випадкових величин (х,у) визначається за формулою

. (4.47)

Статистичний коефіцієнт кореляції 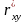обчислюють за формулою

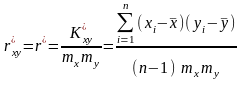, (4.48)

де m_x та m_y обчислюють за формулами

; (4.49)

. (4.50)

Коефіцієнт кореляції знаходиться в межах

-1 £ £ +1.

Якщо коефіцієнт кореляції близький до ±1, то між випадковими величинами існує прямолінійний зв’язок. Рівняння регресії визначають за формулами

,

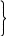
або 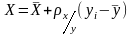(4.51)

де 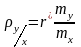; 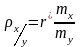- коефіцієнти регресії.

Приклад 3. Коефіцієнт К_і нитяного віддалеміра визначався на різних відстанях D_і від точки установки приладу. Обчислити числові характеристики системи випадкових величин (D,К): математичні сподівання, дисперсії та коефіцієнт кореляції. Результати експерименту наведені в табл. 4.5

Таблиця 4.5

Д(м)	20	40	60	80	100	120	140	160
К	99.0	98.5	99.5	99.0	99.5	99.6	101.0	99.9

Розв’язання. Для наочності обчислення зведемо в табл.4.6

Таблиця 4.6

D визначено в сотнях метрів

№ п/п	D	K	Di -	Ki -	(Di - )2	(Ki- )2	(Di- ) (Ki - )
1	0,2	99,0	-0,7	-0,5	0,49	0,25	+0,35
2	0,4	98,5	-0,5	-1,0	0,25	1,00	+0,50
3	0,6	99,5	-0,3	0	0,09	0	0
4	0,8	99,0	-0,1	-0,5	0,01	0,25	+0,05
5	1,0	99,5	+0,1	0	0,01	0	0
6	1,2	99,6	+0,3	+0,1	0,09	0,01	+0,03
7	1,4	101,0	+0,5	+1,5	0,25	2,25	+0,75
8	1,6	99,9	+0,7	+0,4	0,49	0,16	+0,28
		S	0	0	1,58	3,92	+1,96

Спочатку по формулами (4.43) і (4.44) обчислюють середні арифметичні і

; .

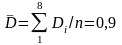В графах 3 і 4 таблиці 4.5 обчислюють відхилення D_i і К_і від середніх арифметичних і .

Контроль: суми відхилень повинні дорівнювати нулю, або величині, що обумовлена помилкою закруглення середніх і .

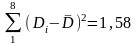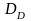Далі в графах 5 і 6 обчислюють квадрати відхилень і їх суми: та . Це дозволяє за формулами (4.45) і (4.46) визначити дисперсії і та за формулами (4.49), (4.50) статистичні стандарти m_D і m_k

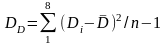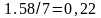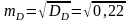= ; = 0,46;

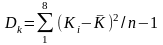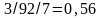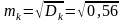= ; = 0,75.

По формулі (4.47) обчислюємо кореляційний момент, а по формулі (4.48) коефіцієнт кореляції

;

.

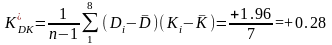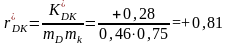Так як r* = 0,81, що досить близько до 1, то можна передбачити, що між величинами D і K існує прямолінійний зв’язок. Спочатку обчислимо коефіцієнт регресії

.

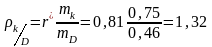По формулі (4.37) рівняння регресії К по D буде

К = 99,5 + 1,32 D - 1,32 × 0,9 ,

або К = 1,32 D + 98,31.

По результатам обчислень можна побудувати графік регресії (рис.4.4)

Рис.4.4

Для побудови прямої регресії обчислено значення двох точок К₁ = 98,31 при D = 0м і К₂ = 99,5 при D = 100 м, які наносимо на графік і проводимо через них пряму лінію.

Такий спосіб визначення оцінок невідомих параметрів називають точковим, а самі оцінки – точковими. Його недоліками є те, що точкова оцінка не збігається з величиною а_і. Це особливо видно при невеликій кількості результатів експерименту. До цього для визначення точності точкової оцінки слід знати і дисперсію