§ 4.4 Числові характеристики статистичного розподілу

Закон розподілу випадкової величини Х характеризує її з ймовірної точки зору. Між тим при вирішенні багатьох практичних задач достатньо знати тільки окремі її числові характеристики, що відображають найбільш істотні риси розподілу випадкової величини.

Ми уже познайомилися з основними числовими характеристиками випадкових величин: математичним сподіванням, дисперсією, початковими та центральними моментами, асиметрією та ексцесом.

Для статистичного розподілу існують такі ж самі числові характеристики. Справа зводиться до того, щоб по результатам експериментів знайти формули їх обчислень.

Так аналогічно для математичного сподівання випадкової величини Х є середнє арифметичне результатів спостережень випадкової величини біля якого ґрунтуються її можливі значення

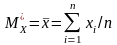, (4.23)

де х_і – значення випадкової величини в кожному і-ому досліді;

n – кількість дослідів.

Величину називають статистичним середнім випадкової величини Х. Слід зазначити, що при досить великій кількості дослідів п статистичне середнє 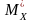або наближається до математичного сподівання випадкової величини Х і може бути прийнятим замість нього, тобто

= » М_Х.

Аналогією дисперсії випадкової величини Х є статистична дисперсія, що обчислюється за формулою

. (4.24)

В методі моментів обчислюють статистичні початкові та центральні моменти будь-якого порядку за формулами

; (4.25)

. (4.26)

Для статистичного ряду розбитого на групи, тобто для статистичної сукупності маємо

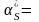
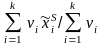; (4.27)

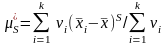, (4.28)

де n_і - кількість результатів в і-ій групі;

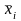- статистичне середнє і-ої групи;

- загальне статистичне середнє.

Аналіз формул (4.20), (4.21) і (4.22) показує, що середнє арифметичне » М_Х, а статистична дисперсія m² » D_X, тобто вони будуть найбільш вірогідними оцінками параметрів закону нормального розподілу.

Слід зазначити, що при виведенні формул в ММП передбачали, що результати експерименту незалежні і проводились в однакових умовах. Тобто комплекс умов: об’єкт, суб’єкт, прилад, зовнішнє середовище і метод вимірювання були незмінними. Такі виміри називають рівноточними. При цьому дисперсії окремих вимірів будуть однаковими, тобт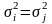о або .

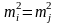Це дозволяє нам стверджувати, що при рівноточних вимірах найближчим значенням вимірюваної величини є середнє арифметичне (формула 4.20), а значенням дисперсії буде 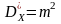(формули 4.21 та 4.22).

Проте на практиці не завжди можна зберегти незмінність комплексу умов. Тоді кожен результат експерименту буде дещо відрізнятися по точності і кожній випадковій величині 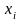буде відповідати своя дисперсія , тобто статистичний ряд буде мати вигляд

х₁, х₂, ... , х_п,

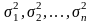. (4.29)

Такі виміри, коли дисперсії ¹ , називають нерівноточними.