Сутність ммп полягає в тому, що за якісну оцінку параметра а беруть таке значення аргументу, що приводить функцію l до максимуму. Рівняння (4.14) розв’язують при умові
.
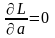(4.15)
При цьому вибирають таке визначення а, яке зводить функцію l до максимуму. Для спрощення функцію правдоподібності заміняють логарифмом, тоді
.
(4.16)
Якщо закон розподілу має два параметри: а1 і а2, то оцінки їх визначають із сумісного розв’язання двох рівнянь
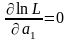і
.
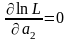(4.17)
Приклад 1. При експериментальних випробуваннях точності розробленого приладу отримана вибірка із генеральної сукупності x1,x2,…,xn. Результати вимірів хі незалежні між собою. Попередні розрахунки показали, що статистична функція (гістограма) має вигляд щільності нормального розподілу. Необхідно знайти оцінку для невідомого параметра а = МХ, що відображає ймовірне значення шуканої величини Х.
Розв’язання. Так як результати експерименту підпорядковуються нормальному закону розподілу, то висунемо умову, що щільність розподілу кожної із величин j (хі, а) залежить від параметра а. Це означає, що для кожної величини функції правдоподібності буде
.
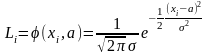Тоді функція правдоподібності для всієї вибірки буде
L(x1
,x2,…,xn,
a
)
=
.
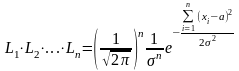Візьмемо логарифм, тоді
.
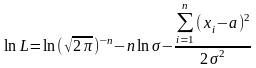За допомогою формули (4.16) отримаємо
.
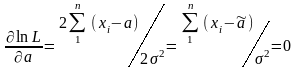При цьому необхідно щоб s2 ¹ 0, тоді
,
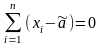або
.
Оцінкою невідомого параметру а буде
.
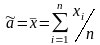(4.18)
Таким
чином надійним значенням параметра а
буде проста
арифметична середина
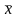із результатів експерименту.
Приклад 2. Згідно умов приклада 1 результати вибірки підпорядковуються закону нормального розподілу. Необхідно визначити оцінки а1 = МХ, а2 = s2, що характеризують величину і дисперсію вибірки.
Розв’язання. Згідно формули щільності закону нормального розподілу з параметрами а1 = МХ і а2 = s2 для кожної випадкової величини хі функція правдоподібності буде
,
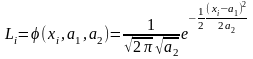а для всієї вибірки
.
Згідно формули (4.17) отримаємо два рівняння і прирівняємо їх до нуля
;
,
або
;
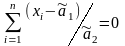а)
(4.19)
.
б)
Із сумісного їх розв’язання отримаємо
;
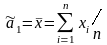(4.20)
.
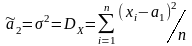(4.21)
Як видно, що перший параметр буде простою арифметичною серединою (формула 4.18), а другий параметр буде статистичною дисперсією (§ 4.4).
Проте виявляється, що при невідомому значенні істинного (ймовірного) значення шуканої випадкової величини Х оцінка дисперсії буде дещо зміщеною. Тому при заміні математичного сподівання МХ простою арифметичною серединою незміщеною оцінкою дисперсії буде
.
(4.22)
В математичній обробці результатів вимірів вираз (4.21) називають формулою Гаусса, а (4.22) – формулою Бесcеля.
Метод максимальної правдоподібності приводить до визначення досить доброякісних оцінок, хоч іноді і зміщених. Проте практично можуть виникати досить складні системи рівнянь.