ГЛАВА ІІ. ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ СТАТИСТИКИ

РОЗДІЛ 4. СТАТИСТИЧНА ОЦІНКА ПАРАМЕТРІВ РОЗПОДІЛУ

§ 1. Основні поняття і задачі математичної статистики. Генеральна сукупність та вибірка

Математична статистика – дисципліна, яка займається регістрацією, збором, описом і аналізом експериментальних даних з метою вивчення закономірностей масових випадкових явищ.

Таким чином, всі задачі математичної статистики зводяться до визначення методів обробки результатів експериментальних досліджень(спостережень) масових випадкових явищ.

Найбільш типовими задачами математичної статистики є:

1. Оцінка невідомої функції розподілу по результатам вимірів. Якщо по результатам досліджень випадкової величини Х одержано значення х₁, х₂, ..., х_п, то необхідно приблизно оцінити невідому функцію розподілу F(x).

2. Оцінка точності невідомих параметрів розподілу. При вирішенні цього питання обчислюють параметри функції розподілу випадкової величини на основі отриманих результатів експерименту і оцінюють їх значення.

3. Статистична перевірка гіпотез. Якщо за результатами експерименту визначено функцію розподілу F(x) випадкової величини Х, то вирішується питання: чи дійсно випадкова величина Х має розподіл F(x) ?

При дослідженнях випадкових явищ виконують досить велику кількість випробувань (експериментів) – N. Сукупність значень результатів досліджень (вимірів) називають генеральною сукупністю. Досить часто мають на увазі, що число N може бути нескінченним.

Проте практично виконати нескінченну кількість дослідів (вимірів), або обстежити нескінченну кількість виробів неможливо і економічно невигідно. В цьому випадку із всієї генеральної сукупності відбирають обмежене число результатів експерименту.

Сукупність випадково вибраних результатів чи об’єктів називають вибірковою сукупністю, або просто вибіркою.

Проте вибірка може як досить точно характеризувати досліджуване випадкове явище, так і ні. Якщо об’єм вибірки п із генеральної сукупності N дозволяє в повній мірі визначити характеристики генеральної сукупності, то її називають представницькою або презентабельною вибірковою. Інформація буде більш імовірною, коли результати досліджень, що складають вибірку, будуть незалежними.

§ 2. Розподіл статистичних рядів

Практично до постанови досліджень випадкового явища заздалегідь невідомо якому закону розподілу будуть підпорядковуватися результати експерименту. Для його визначення над випадковою величиною Х виконується ряд незалежних експериментів (вимірів). Результати вимірів х₁, х₂, ..., х_п і їх номер можна подати у вигляді статистичної таблиці 4.1

Таблиця 4.1

і	1	2	3	4	...	п
хі	х1	х2	х3	х4	...	хп

Статистична таблиця є початкова форма запису статистичного матеріалу. Він може оброблятися різними методами.

Однак при великій кількості експериментів (вимірів) їх результати практично неможливо показати в статистичній таблиці. Тоді результати спостережень розділяють на групи. Кожна група містить деяку кількість (частоту) результатів, що належать визначеному інтервалу. Довжина інтервалу розраховується за формулою Г.А.Стерджеса

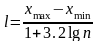, (4.1)

де п – кількість результатів спостережень.

Можна задатись числом інтервалів k. Тоді довжину інтервалу визначають за формулою

. (4.2)

Значення інтервалу l заокруглюють до зручного цілого значення так, щоб число їх було в границях .

Потім визначають граничні значення інтервалів за формулами

д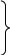 ля 1- ої групи ; ;

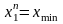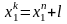для 2 -ої групи ; ;

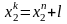------------------------------- , (4.3)

для k-ої групи ; .

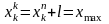де 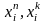- відповідно початкове та кінцеве значення абсциси х (результатів вимірів).

Для кожної групи підраховують частоту результатів n_і, які попадають в граничні значення 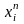і 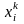і статистичну ймовірність за формулою

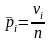, (4.4)

причому n₁ + n₂ + ...+ n_k = n; .

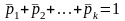За допомогою статистичної таблиці, або статистичної сукупності можна побудувати статистичну функцію розподілу випадкової величини Х.

Статистичною функцією розподілу випадкової величини Х називається закон по якому змінюється частота події Х < x в даному статистичному матеріалі, тобто

. (4.5)

Як видно, що частота n_і практично пропорційно співвідноситься з ймовірністю попадання випадкової величини Х в кожну і-у групу, визначеної на основі статистичного матеріалу. Тоді значення статистичної функції розподілу згідно формули (4.5) обчислюються за формулою

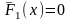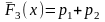; ; , ... , = 1. (4.6)

Крім того, можна обчислити статистичну щільність розподілу для кожної групи за формулою

. (4.7)

Обчислені дані використовують для побудови графічного зображення статистичної функції. Для цього по осі абсцис відкладають граничні значення груп . Якщо по осі ординат відкласти значення частот n_і і отримані точки з’єднати ламаною лінією, то отримаємо полігон частот (рис.4.1). При відкладені значень 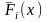отримують сходинковий графік (рис.4.2), а при 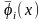- гістограму (рис.4.3).

Приклад. Припустимо, що отримана статистична сукупність 100 похибок вимірів довжини лінії за допомогою електронного віддалеміра.

Розв’язання. За допомогою формул (4.1) – (4.7) зроблені необхідні обчислення і занесені в табл. 4.2.

Таблиця 4.2

l = 5; k = 8

№ групи Граничні значення	1	2	3	4	5	6	7	8	S
від до (мм)	-20 -15	-15 -10	-10 -5	-5 0	0 5	5 10	10 15	15 20	-
nі	2	8	17	24	26	13	6	4	100
	0,02	0,08	0,17	0,24	0,26	0,13	0,06	0,04	1,0
	0,02	0,10	0,27	0,51	0,77	0,90	0,96	1,00	-
	0,004	0,016	0,034	0,048	0,052	0,026	0,012	0,008	-