Экскурс в модифицированный симплекс-метод
В модифицированном и табличном симплекс-методах выбор переменной, выводимой из множества базисных, осуществляется с помощью соотношения:
(11)
где p - номер вводимой в базис переменной (в ТЗ это пара индексов ),
i
множеству номеров базисных
переменных (в ТЗ:
),
q
- номер выводимой из базиса переменной
(в ТЗ это пара индексов
),
и
определяется сл.о.:
(в ТЗ:
),
а
-
столбец, соответствующий вводимой в
базис переменной (в ТЗ:
).
Отметим также, что соотношение (11) дает и само значение вводимой переменной.
Покажем, что соотношение (10) - это соотношение (11) в условиях ТЗ.
С учетом теоремы 3 (Любой
минор матрицы
Р
транспортной задачи принимает одно из
трех числовых значений 0, 1 или -1)
можно показать, что компоненты вектора
(
) также принимают только одно из
трех значений 0,
1 или -1
и при этом подмножество базисных
переменных, у которых
>0,
соответствует подмножеству пар индексов
.Тогда,
с учетом обозначений индексов
вводимой и выводимой переменных
транспортной задачи, (11)
имеет вид:
,
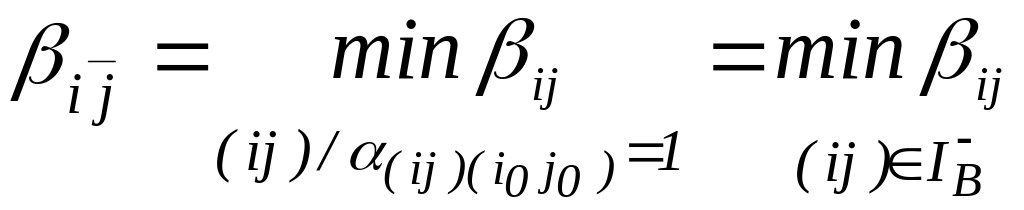что с точностью до обозначений
соответствует (10) (т.к.
,
среди которых ищется минимум, -
значения базисных переменных с индексами
из подмножества пар индексов
).
Отметим также, что подмножеству базисных
переменных, у которых
=
-1
соответствует подмножеству пар индексов
.
У остальных базисных
переменных (не вошедших в цикл)
=
0.
5.3.4. Переход к новому бдр
При рассмотрении способа перехода от ДБР { } i=1..m, j=1..n к другому в модифицированном С-М мы пользовались следующими соотношениями:
(12)
Здесь
- значение i-й
базисной переменной тогда, когда вводимая
небазисная переменная принимает значение
.
Построим соотношение (12)
для ТЗ (1)-(3) с учетом (10)
(=
)
и того, что
=
-1, 0, 1:
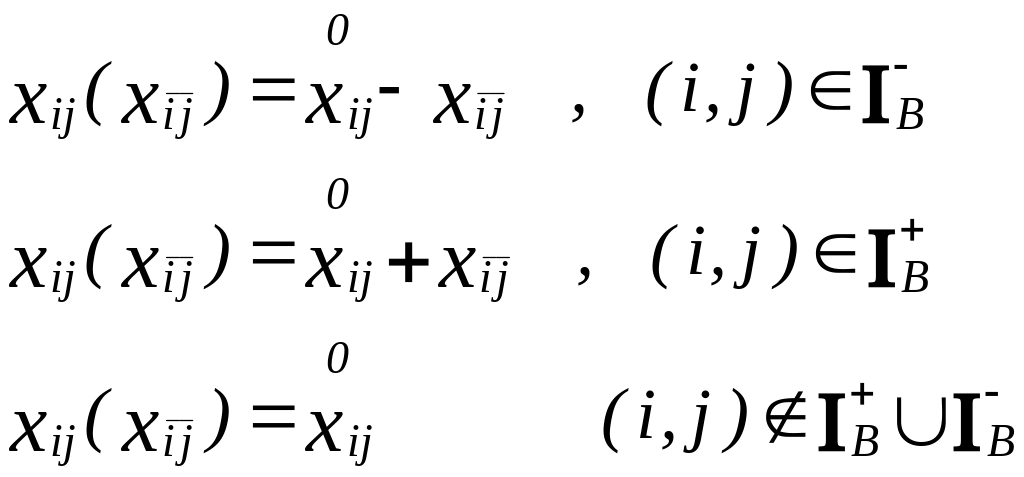(13)
5.5. Схема метода потенциалов
Всеми предыдущими рассуждениями обоснована последовательность шагов метода потенциалов решения ТЗ.
ШАГ 0 Построение начального ДБР.
Построить начальное ДБР { } исходной задачи (методом северо-западного угла, методом минимальной стоимости и т.п.)
Пусть
- множество пар индексов базисных
переменных начального ДБР.
ШАГ 1 Вычисление относительных оценок небазисных переменных
По множеству построить систему уравнений:
Найти решение {
}
i=1..m,
{
}
j=1..n
такой системы с точностью до слагаемого.
Вычислить относительные оценки
:
=
+
-
(i,j)
ШАГ 2 Проверка условия оптимальности.
Если 0 для всех (i,j) , то прекратить вычисления, текущее ДБР является решением исходной задачи.
ШАГ 3 Выбор небазисной переменной, вводимой в множество базисных
Выбрать пару
такую, что
>0
переменную
будем вводить в базис
ШАГ 4 Выбор базисной переменной, выводимой из множества базисных
Для переменной
построить компенсаторный цикл.
Выделить множества
и
.
Выбрать
.
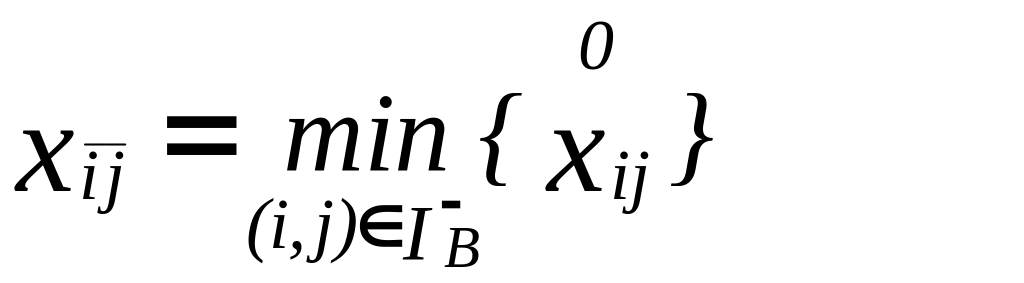ШАГ 5 Переход к новому ДБР.
Определить новое ДБР с помощью соотношений (13):
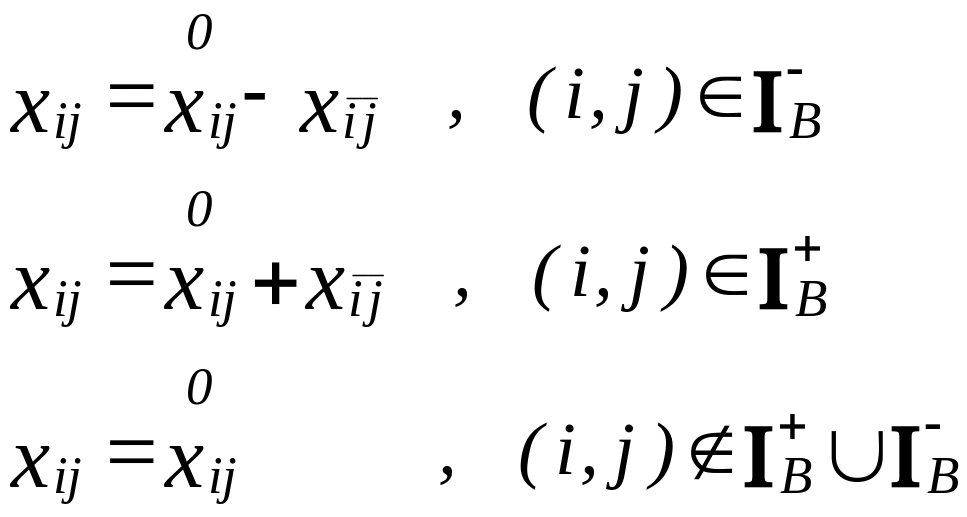
(Остаются неизменными и все, кроме вводимой, небазисные переменные).
Построить новое множество пар индексов базисных переменных:
,
положить
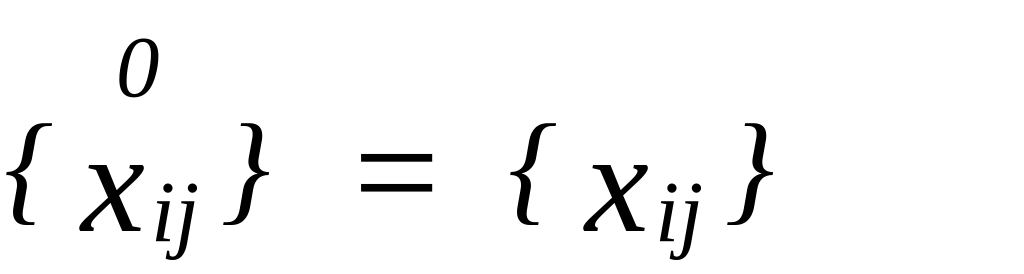и перейти на ШАГ
1
В схеме метода потенциалов (МП) отсутствует проверка условия неограниченности ЦФ на множестве допустимых решений
Самостоятельно №9.
объяснить смысл проверки условия неограниченности ЦФ на множестве допустимых решений в модифицированном С-М и показать, почему она не нужна в МетодеПотенциалов.
ТЕОРЕМА 9.
если
все
и
-
целые, то решение транспортной задачи,
полученное методом потенциалов,
целочисленно.
Доказать самостоятельно №10.