Транспортная задача
5.3. Этапы метода потенциалов
Название этого метода основывается на физическом аналоге ТЗЛП, построенном с помощью понятия потенциального поля. Метод потенциалов по существу является модифицированным симплекс-методом. Следовательно, он имеет три следующих этапа:
выбор переменной, вводимой в базис;
выбор переменной, выводимой из базиса;
переход к новому ДБР.
Пусть исходная ТЗЛП задана в векторной форме:
Утверждение 1.
С учетом того, что любое
из ограничений (2) является линейной
комбинацией остальных n+m-1,
для линейной независимости векторов
в системе ограничений (2) должно быть
отброшено одно ограничение.
5.3.1. Выбор переменной, вводимой в базис Экскурс в модифицированный симплекс-метод
Выбор переменной, вводимой в базис зависит от значений компонент вектора относительных оценок, который в модифицированном СМ определяется следующим образом:
(в нашем случае
)
где
-
вектор оценок ограничений
(двойственных переменных):
Вектор
является решением следующей системы
линейных уравнений:
после транспонирования получим:
(6)
Для каждого ДБР находим по формуле (5) или из системы (6) значения оценок ограничений, подставляем их в (4) и выясняем, является ли оно оптимальным.
Рассмотрим теперь модифицированный С-М применительно к ТЗЛП.
Представим вектор
оценок ограничений (2) ЗЛП
(1)-(3) в ви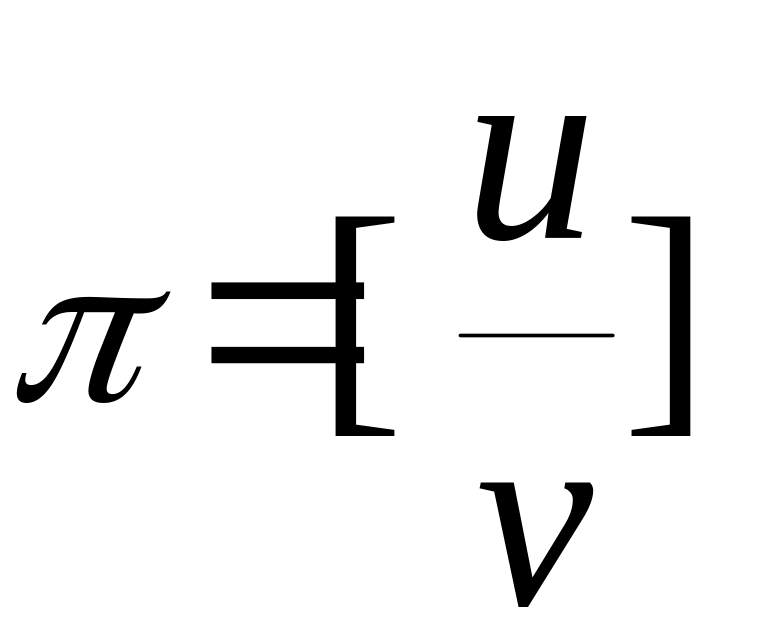де
,
где
соответствует m
первым ограничениям, связанным с
производителями, а
- соответствует n
последним ограничениям , связанным с
потребителями. И построим
для задачи (1)-(3) систему (6), записанную
по уравнениям (для упрощения изложения
утверждение 1 учтем немного позже):
где
- множество пар индексов
базисных переменных.
С учетом такой структуры
вектора
:
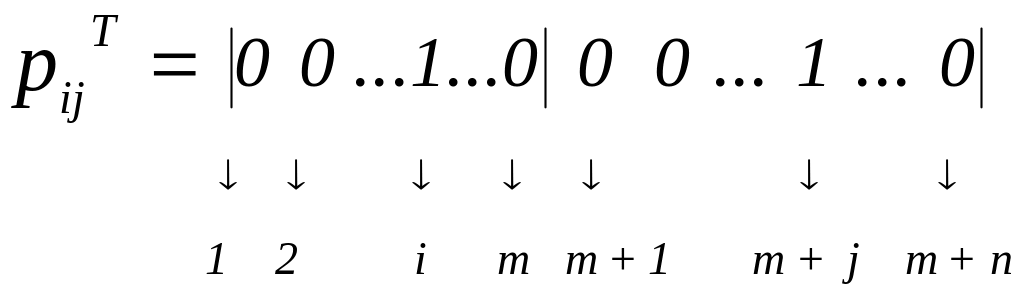
получим:
где
- i
– я компонента вектора
,
j–
я компонента вектора
.
Система (8) имеет m+n переменных и m+n -1 уравнение.
В силу утверждения 1 в
системе ограничений ТЗ одно из ограничений
лишнее. Отбросить его - значит придать
соответствующей ему двойственной
переменной произвольное значение
(проще всего приравнять нулю). Т.к. лишним
можно считать любое из уравнений, то
значение "нуль" можно придать
любой из переменных
или
.
Пусть
=0.
После этого система (8)
превращается в систему из
m+n-1 уравнений с
m+n-1
переменными.
Система (8) решается
элементарно, т.к. имеет специальную
структуру: в каждом уравнении только 2
неизвестных , одно
и
одно
.
Можно показать, что если вычислять
значения переменных
и
в определенном порядке, то каждое
последующее уравнение будет содержать
лишь одно неизвестное.
Пусть
- решение системы (8). Тогда,
учитывая (4), можем определить относительные
оценки
небазисных
переменных:
=
+
-
Ecли все
0, то заданное
БДР оптимально, если есть
>0,
то нужно переходить к следующему БДР.
Существует второй
путь (с использованием теории
двойственности) получения
значений потенциалов
и
(которые в конечном счете входят в
выражение для определения компонент
вектора относительных оценок
).
На єкзамен
Вспомним, что оценки ограничений прямой задачи являются переменными двойственной задачи. Построим задачу, двойственную к исходной. Пусть для ограничений, соответствующих пунктам производства, двойственные переменные обозначены через , а для пунктов потребления - через .
Специфика структуры ограничений двойственной задачи (ДвЗ) определяется особенностью распределения нулей и единиц в соответствующих соотношениях прямой задачи:
Каждое ограничение включает лишь одну переменную и одну переменную .
кроме того, в каждом ограничении ДЗ индексы переменных и совпадают с двойным индексом коэффициента c. Поэтому, если
,
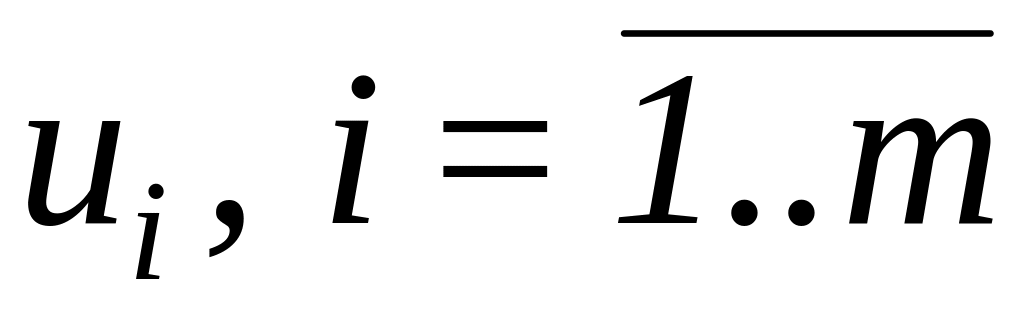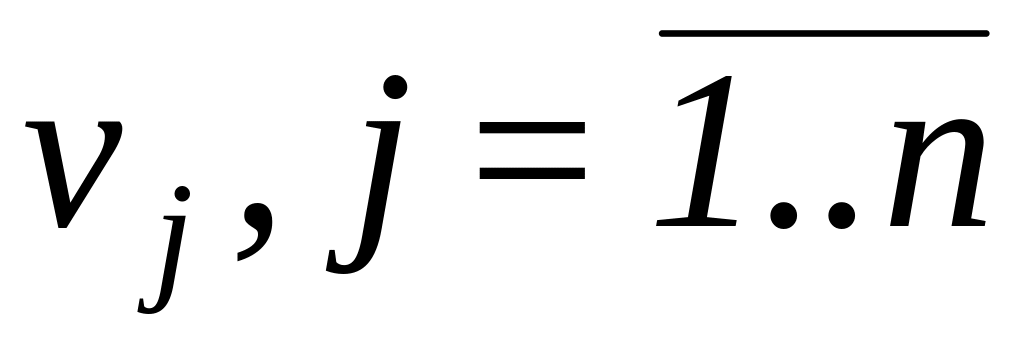- двойственные переменные, соответствующие
ограничениям для i-го
пункта производства и j-го
пункта потребления,
т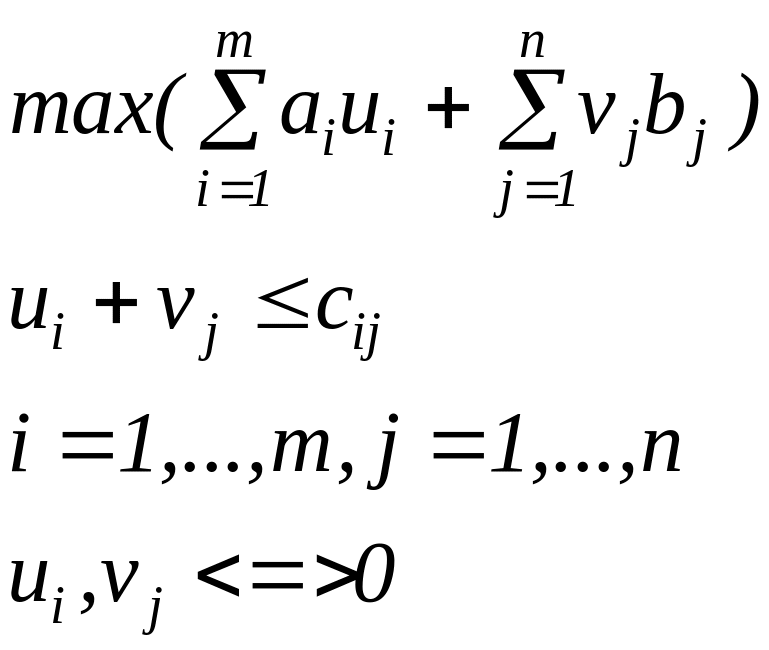
огда
двойственная задача (ДвЗ)
формулируется следующим образом.
Из теории двойственности следует, что для всех базисных переменных прямой задачи соответствующие ограничения двойственной задачи должны удовлетворяться в форме равенств [6] :
(где пара (i,j) пробегает все множество пар индексов базисных переменных).
При реализации С-М процедура решения начинается с установления допустимого, но неоптимального решения прямой задачи. В процессе последующих итераций текущие решения задачи остаются допустимыми и улучшаются до тех пор, пока не будет получено оптимальное решение. Это эквивалентно такой последовательности двойственной задачи, в которой начальное решение является недопустимым, но оптимальным ("лучшим, чем оптимальное"). В процессе дальнейших итераций происходит приближение к допустимому решению при сохранении оптимальности (по критерию оптимальности). Указанное соотношение эквивалентности следует из того, что неоптимальность решения прямой задачи (минимизации) связана с условием
по
крайней мере для одной из базисных
переменных. Это свидетельствует о том,
что соответствующее решение двойственной
задачи не является допустимым. В точке,
где все значения
удовлетворяют условию оптимальности,
решение двойственной задачи автоматически
становится допустимым. [6]
С учетом всего вышеизложенного можно сформулировать следующую теорему.
Теорема 7.
Для того, чтобы
некоторое решение {
}
транспортной задачи (1)-(3) было оптимальным,
необходимо и достаточно, чтобы существовала
система m+n
чисел
,
, которые удовлетворяли бы следующим
условиям:
для всех занятых
клеток транспортной таблицы,
для всех свободных
клеток.
Самостоятельно №6 Сопоставить число элементарных операций (сложения и умножения), необходимых для определения переменной, вводимой в базис, в модифицированном СМ и методе потенциалов.
Самостоятельно
№7
Показать, как изменятся
если принять
=const0.