Транспортная задача
5. Метод потенциалов
Метод потенциалов - один из наиболее часто используемых методов решения ТЗЛП. Этот метод является реализацией модифицированного симплекс-метода в условиях транспортной задачи. ТЗЛП:
Далее ТЗЛП будем задавать таблицей:
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
... |
|
|
... |
... |
... |
... |
... |
|
|
|
|
|
|
|
... |
|
|
|
|
... |
|
|
5.1. Методы построения начального дбр
Решение ЗЛП симплекс-методом начинается с некоторого допустимого базисного решения (ДБР). В методе потенциалов используются следующие способы нахождения начального ДБР:
метод северо-западного угла;
метод минимальной стоимости;
метод Фогеля.
5.1.1. Метод северо-западного угла
Шаг 1.
Придаем переменной
(расположенной в северо-западном углу
транспортной таблицы) максимальное
значение, допускаемое ограничениями
на спрос и объем производства:
Шаг 2.
Если
,
то производитель 1 полностью использовал
свои возможности и далее его можно
не учитывать,
а потребность 1-го потребителя
теперь будет равна:
;
Если
, то 1-й потребитель полностью удовлетворил
свою потребность в продукции
и его можно дальше не
учитывать, а производитель
1 теперь располагает лишь
единицами продукции;
Если
,
то из рассмотрения можно исключить и
потребителя и производителя. В этом
случае исключается ("выбывает из
игры") только один
из них: либо производитель , либо
потребитель, а оставшемуся потребителю
(производителю) приписывается нулевой
спрос (объем производства).
Шаг 3. После установления объема перевозок по маршруту (1,1) мы имеем дело с новой задачей, в которой суммарное число производителей и потребителей на 1 меньше, чем в исходной. В северо-западную клетку таблицы новой задачи, полученной мысленным вычеркиванием первого столбца или первой строки старой таблицы, снова помещаем максимально возможный объем перевозок ( он может оказаться и нулевым).
Продолжая этот процесс,
придем к допустимому решению задачи,
т.к.
ПРИМЕР
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
1 |
100 |
|
|
|
|
100 |
-- |
|
|
2 |
20 |
130 |
|
|
|
150 |
130 |
-- |
|
3 |
|
70 |
100 |
30 |
0 |
200 |
130 |
30 |
0 -- |
4 |
|
|
|
|
100 |
100 |
-- |
|
|
|
120 |
200 |
100 |
30 |
100 |
550 |
-- |
|
|
|
20 |
70 |
-- |
-- |
100 |
|
|
|
|
|
-- |
-- |
|
|
-- |
|
|
|
|
Итак, ДБР, полученное методом северо-западного угла:
остальные
Покажем, что метод северо-западного угла всегда приводит к ДБР ( и, следовательно, начиная с него, можно далее использовать для нахождения оптимального решения симплекс-метод)
ТЕОРЕМА 5.
Метод северо-западного угла всегда приводит к ДБР.
Доказательство.
Нам нужно доказать, что
(А) векторы
,
соответствующие всем заполненным в
процессе отыскания допустимого решения
клеткам, включая и клетки, в которых
вписаны нули, линейно-независимы
и
(Б) их количество равно m+n-1 (рангу матрицы Р).
(В нашем примере это были бы
векторы
).
Мы помним, что столбец
коэффициентов при
имеет вид:
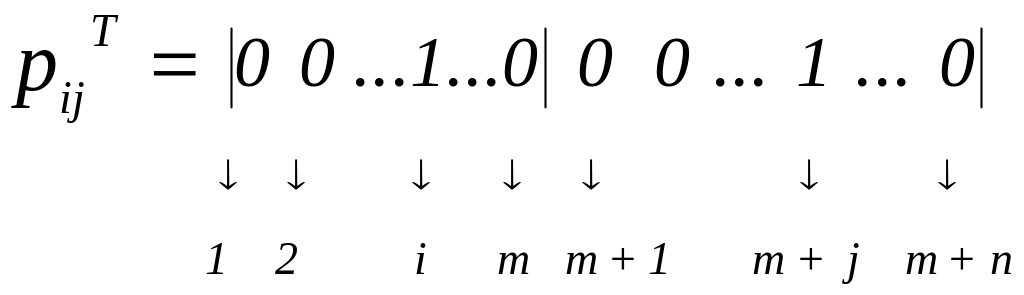
О ДБР задачи можно говорить
только тогда, если все ее ограничения
- уравнения линейно-независимы. Поэтому
исключим из рассмотрения одно из
уравнений, например, первое. Это
соответствует тому, что у всех
рассматриваемых векторов мы отбросим
первую координату. Полученные
вектора обозначим через
.
Представим схематически все возможные варианты последовательного заполнения клеток по методу северо-западного угла.
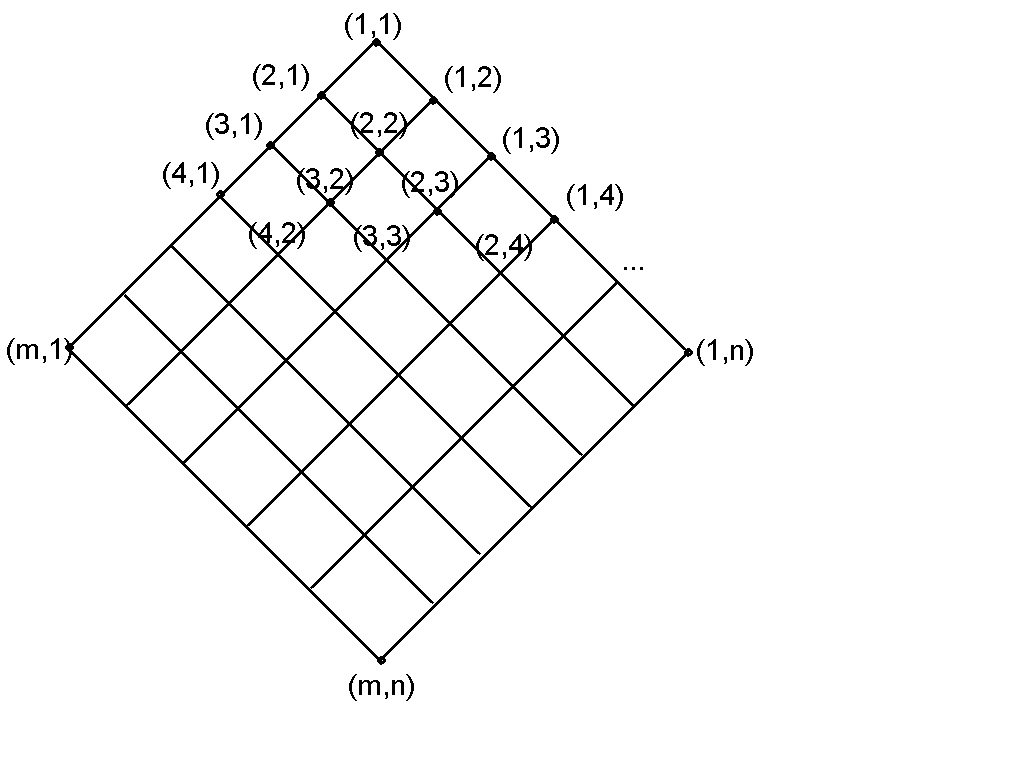
Поскольку все варианты в этом смысле равноценны, доказательство приведем только для одного из них, например, самого правого в нашей схеме. Этому варианту соответствует следующий набор векторов:
.
Соответствующая транспортная таблица имеет вид:
-
x
x
x
x
x
x
x
x
x
x
Сначала докажем (Б).
(Б) Так как на каждом шаге метода суммарное число производителей и потребителей уменьшается только на 1, то когда мы от исходной их суммы m+n дойдем до суммы, равной 2, будет заполнено m+n-2 клетки. Но сумма, равная 2, означает, что остался только один производитель и только один потребитель, т.е. последняя таблица состоит только из одной клетки, которую мы и заполняем. Таким образом, следуя методу северо-западного угла мы всегда заполняем ровно m+n-1 клетку.
(А) Набор соответствующих этим клеткам векторов состоит из m+n-1 вектора. Векторы (m+n -1)-мерны. Поэтому матрица , составленная из них, квадратная. В нашем случае она имеет вид:
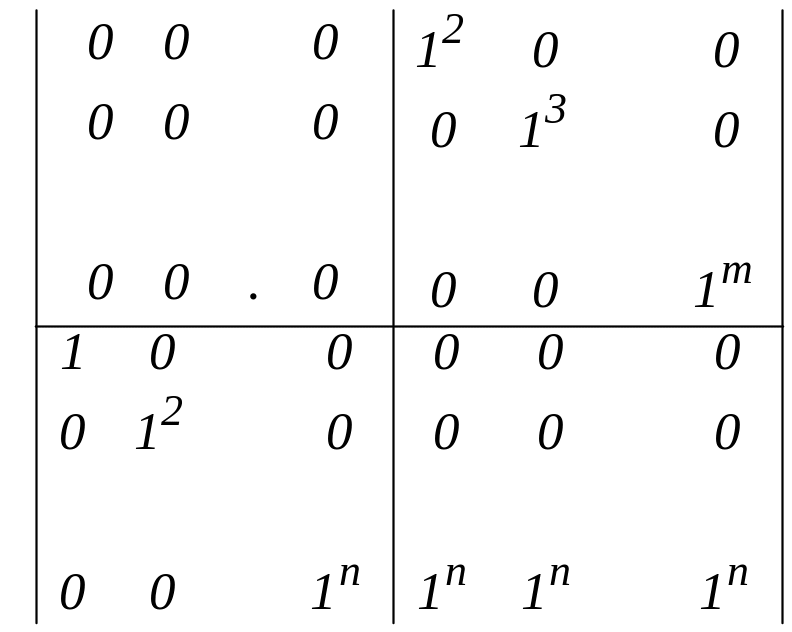
m-1
n
n m-1
Для квадратной матрицы линейная независимость столбцов вытекает из линейной независимости строк (и наоборот).
Самостоятельно №2 Доказать линейную независимость строк этой матрицы.
При построении исходного
ДБР методом северо-западного угла никак
не учитываются удельные затраты на
перевозку продукции
.
Между тем, представляется вероятным,
что чем больше в начальном ДБР "дешевых"
перевозок, тем ближе это решение к
оптимальному. Методы построения
начального ДБР, такие как метод наименьшей
стоимости и приближенный алгоритм
Фогеля учитывают
значения
и обычно дают
лучшее, чем метод северо-западного угла,
начальное решение.