Практическая работа №4. Задача о назначениях

Важной разновидностью транспортной задачи ЛП, является т. н. «задача о назначениях» Суть ее сводится к следующему. Пусть имеются n кандидатов и n работ.

Известны затраты с_ij , связанные с выполнением i -м кандидатом j - й работы. Предполагается, что каждый кандидат может быть назначен только на одну работу и каждая работа может быть выполнена только одним кандидатом.

Требуется так распределить (назначить) кандидатов на работы, чтобы суммарные затраты были минимальны.

Эта задача возникает, например, при распределении работников фирмы на обслуживание клиентов, при распределении водителей по автомашинам, при распределении групп студентов по аудиториям и т.д.

Построение математической модели:

х_{i j} =1, если i -й кандидат назначен на j- -ю работу

х_{i j} =0, в противном случае.

По условию:

- каждый кандидат назначается только на одну работу, j =1,…,n (4.1)

- каждая работа выполняется только одним кандидатом, i = 1,…,n (4.2)

(4.3)

Легко видеть, что модель соответствует модели транспортной задачи и может быть решена стандартным методом, скажем методом потенциалов, однако специальная форма записи модели позволила разработать более эффективный алгоритм решения задачи называемый венгерским методом. Для решения задачи на компьютере может быть использована стандартная процедура поиск решения Microsoft Excel (прил. 4), с той лишь разницей, что вместо свободных членов (запасов) матрицы ограничений транспортной задачи заносятся 1 (каждый кандидат может быть назначен только на одну работу).

Задана матрица затрат:

С =

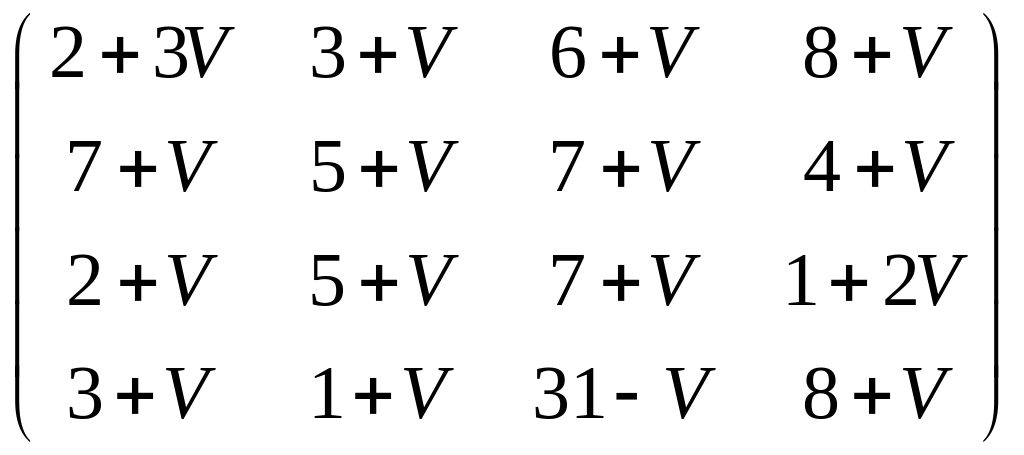
Решить задачу о назначениях.

Ответ представить в графической форме

Практическая работа № 5. Решение задач теории игр сведением к двойственной задаче лп.

Игру двух лиц с нулевой суммой в смешанных стратегиях можно представить парой двойственных задач линейного программирования и решить, например, симплекс-методом.

Предположим игра, задана платежной матрицей

Вычмслим α = max (min ai j ) нижнею цену игры и β = min (max ai j) верхнею цену игры. Проверим на наличие седловой точки, α= 1, β= 2 → игра без седловой точки.

Пусть (р₁, р₂) – смешанная стратегия игрока А, (q₁, q₂, q₃) – смешанная стратегия игрока В. Напомним, что р₁ + р₂ = 1, и q₁ + q₂ + q₃ =1.

Воспользуемся теоремой Неймана утверждающей, что:

Существует такое число v (цена игры), что если игрок А придерживается оптимальной смешанной стратегии, то математическое ожидание его выигрыша (т.е. средний гарантированный выигрыш) будет не меньше v. Аналогичное утверждение относительно игрока В: математическое ожидание его проигрыша будет не больше v.

Для игрока А:

3р₁ + р₂ ≥ v

3р₂ ≥ v (5.1)

р₁ + 2р₂ ≥ v

F = v → max

Преобразуем ограничения, разделив все члены неравенств на v (обозначим y₁ = р₁/v, y₂ = р₂/v, заметим, что v = 1/(y₁ + y₂)).

Итак, задача принимает вид:

3y₁ + y₂ ≥ 1

3y₂ ≥ 1 (5.2)

y₁ + 2y₂ ≥ 1

G = y₁ + y₂ → min

Для игрока B:

3q₁ + q₃ ≤ v

q₁ + 3q₂ +2q₃ ≤ v (5.3)

F = v → min

Преобразуем ограничения, разделив все члены неравенств на v (обозначим х₁ = q₁/v, х₂ = q₂/v, x₃= q₃/v, заметим, что

v= 1/(x₁ + x₂+x₃)).

Итак, задача принимает вид:

3x₁ + x₃ ≤ 1

x₁ + 3x₂ +2x₃ ≤ 1 (5.4)

F = x₁+x₂+x₃ → max

Таким образом получена пара двойственных задач (5.2) и (5.4). Напомним, что, решив одну из них, например, симплекс-методом, мы автоматически найдем решение другой. Для решения задачи может быть использована стандартная процедура поиск решения в среде Microsoft Excel. Формат представления данных и результатов решения приведены в прил. 2.

Решить игру, заданную платежной матрицей, используя сведение к двойственным задачам линейного программирования:

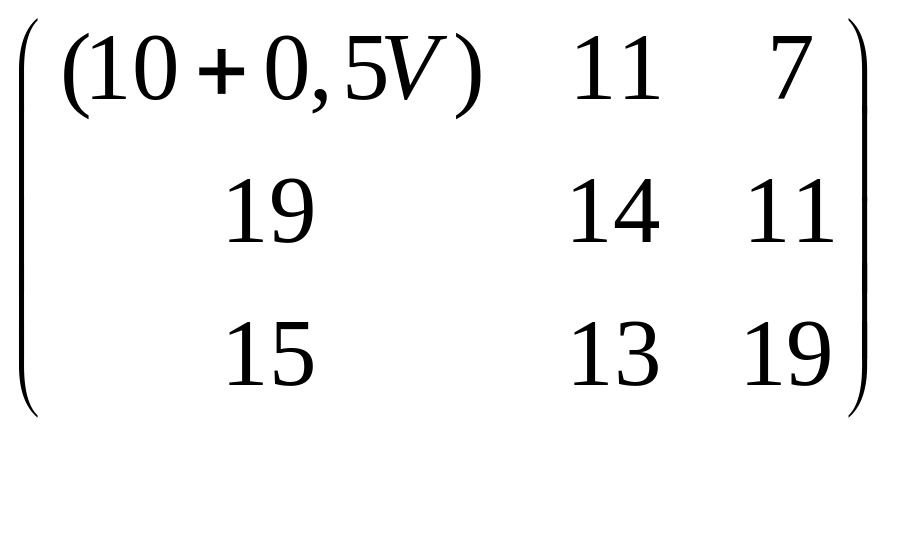
Расчеты выполняются в среде EXCEL