3 Моделирование механической системы средствами пакета matlab

В соответствии с заданием на курсовую работу написана программы математического моделирования инерционного прибора, в которой рассчитываются параметры прибора и строятся графики переходного процесса при единичном входном воздействии. Программа написана средствами пакета MATLAB.

global T dzeta;

m=1e-3*input('Введите значение массы [г] m=');

d=1e-3*input('Введите диаметр проволоки [мм] d=');

ds=1e-3*input('Введите значение среднего радиуса витка [мм] r=');

ni=input('Введите количество витков пружины i=');

f=input('Введите значение коэффициента вязкого трения f=');

G=83670e6; % Модуль упругость второго рода [Па]

nw=ni+0.5; % Число рабочих витков пружины

k=G*d^4/(8*nw*ds^3); % Жесткость пружины

mu=30e-3; % Динамический коэффициент смазки

T=sqrt(m/k); % Период колебаний

dzeta=f/(2*k*T); % Коэффициент демпфирования

y0=[5 0]; % Начальные условия

t0=0.0; % Начальное время

tfin=100*T; % Конечное время

tspan=[t0 tfin]; % Временной интервал моделирования

[t,y]=ode23(@odefun, tspan, y0); % Решение дефференциального уравнения

figure(1)

plot(t,y(:,1)), grid % График переходного процесса

title('Переходной процесс при единичном входном воздействии','FontName','Courier')

xlabel('Время, с','FontName','Courier')

ylabel('Амплитуда колебаний, мм','FontName','Courier')

pause % Эту строку удалить

figure(2) % Открытие нового графического окна

plot(y(:,1),y(:,2)), grid % График фазовой траектории

title('Фазовая диаграмма системы','FontName','Courier')

xlabel('Перемещение, мм','FontName','Courier')

ylabel('Скорость, мм/с2','FontName','Courier')

res(1)=T;, res(2)=dzeta;, res(3)=f;

disp(' T dzeta f');

disp(res);

M- файл (odefun.m) функции пользователя, описывающей систему ОДУ

function ypr=odefan(t,y);

global T dzeta

% Система ОДУ

ypr=[y(2); ((1e-3/T^2)-(y(2).*(2*dzeta/T))-(y(1)./T^2))];

Результаты моделирования представлены ниже (см. рисунок 3-8 ).

T=0.0124 dzeta=0.0531 f=0.3000

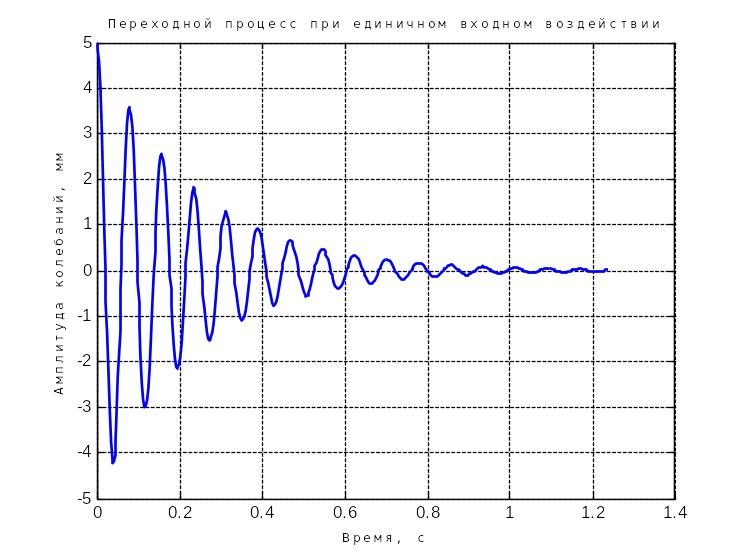
Рисунок 3 – Переходной процесс при начальных условиях

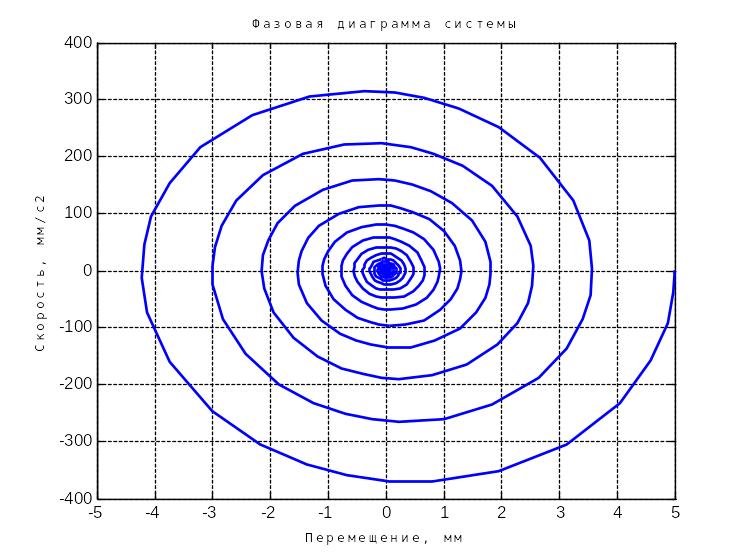
Рисунок 4 – Фазовая диаграмма при начальных условиях

T=0.0124 dzeta=0.2653 f=1.5000

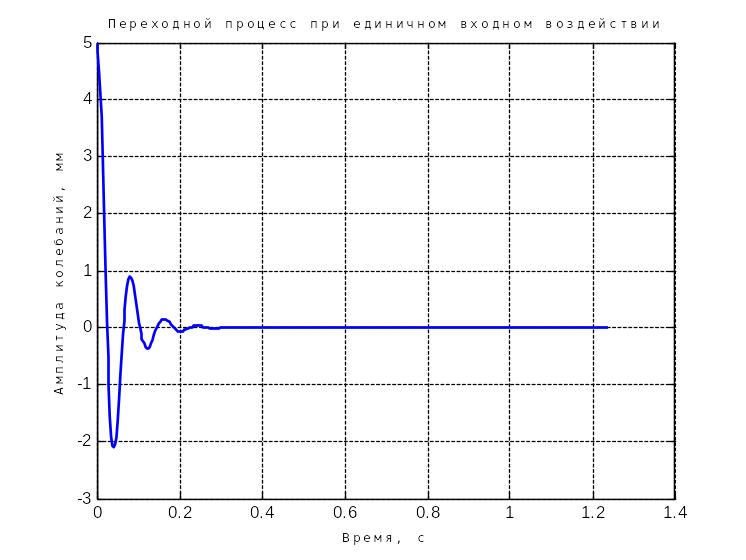
Рисунок 5 – Переходной процесс при >₀

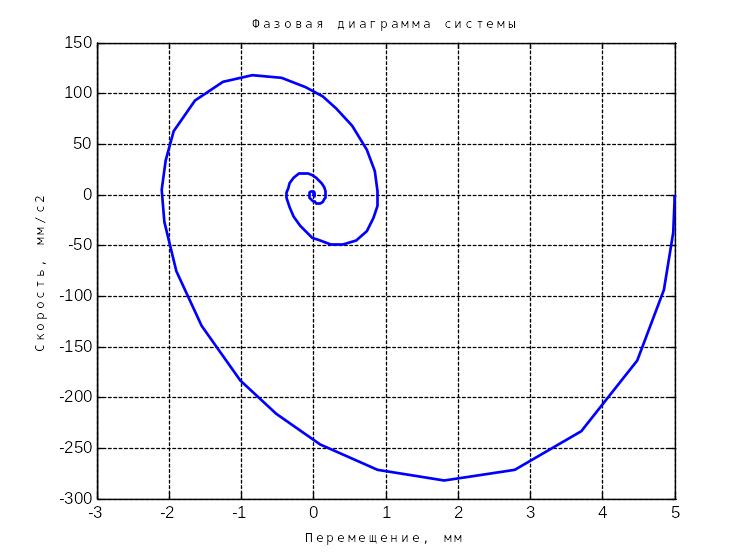
Рисунок 6 – Фазовая диаграмма при >₀

T=0.0124 dzeta=0.0265 f=0.1500

Рисунок 7 – Переходной процесс при <₀

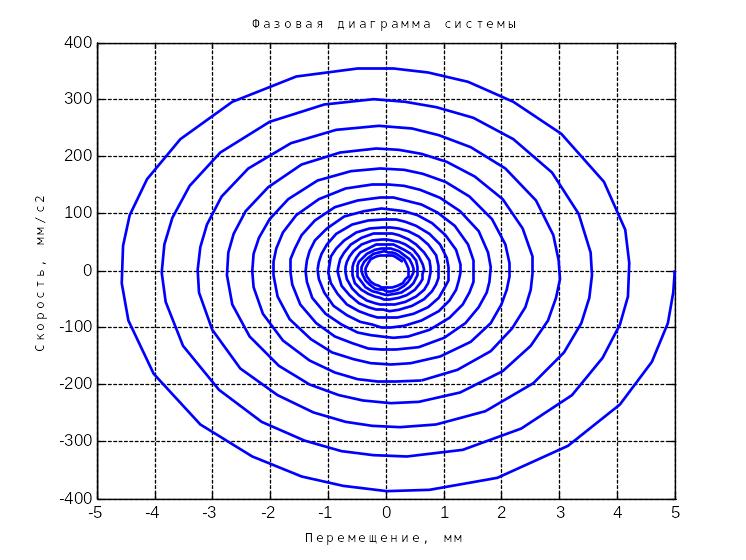
Рисунок 8 – Фазовая диаграмма при <₀

Результаты моделирования позволяют сделать следующие выводы:

1. Рассматриваемая механическая система при начальных условиях представляет собой устойчивое колебательное звено второго порядка.

2. При увеличении коэффициента демпфирования колебания системы сокращаются, и колебания затухают быстрее.

3. Уменьшение значения коэффициента демпфирования (<₀) способствует увеличению процесса затухания колебаний, то есть увеличению времени моделирования.

Список использованных источников

1. Спектор С.А. Электрические измерения физических величин: Методы измерений: Учеб. пособие для вузов. - Л.: Энергоатомиздат, 1987.

2. Зарубин В.С. Математическое моделирование в технике: Учеб. для вузов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.

3. Попов Е.П. Теория линейных систем автоматического регулирования и управления. - М.: Наука, 1989.

4. Дьяконов В.П. MATLAB 6: Учебный курс. - СПб.: Питер, 2002.

13