- •Автор: р. З. Камалян – доктор технических наук, профессор
- •Криволинейные и поверхностные интегралы: Методическая разработка для студентов дневной формы обучения по специальностям:
- •351400 – Прикладная информатика в экономике;
- •1. Чтение учебников и учебных пособий
- •2. Решение примеров
- •3. Самопроверка усвоения изученной темы
- •4. Консультации (письменные и устные)
- •5. Выполнение контрольных работ
- •6. Лекции и практические занятия
- •7. Требования на зачете и экзамене
- •8. Рекомендуемая литература
- •Элементы теории множеств
- •2. Основные операции над множествами
- •3. Свойства операций над множествами
- •4. Декартово произведение множеств
- •5. Отображение множеств. Функции.
- •6. Бинарные отношения.
- •Свойства разложения бинома Ньютона
- •Основные формулы числа сочетаний
- •Решение комбинаторных уравнений
- •5. Элементы теории графов и сетей
- •1. Основные понятия и определения
- •2. Операции над графами
- •3. Деревья. Лес.
- •4. Эйлеровы и гамильтоновы графы
- •5. Плоские и планарные графы
- •6. Матрицы графов
- •7. Понятие сети
- •Алгоритм построения максимального потока.
- •Построить некоторый начальный поток
- •Элементы математической логики
- •Предел математической логики
- •2. Понятие о высказывании
- •3. Основные логические операции
- •4. Равносильность высказываний
- •1. Основные равносильности:
- •2. Равносильности, выражающие одни логические операции через другие.
- •3. Равносильности, выражающие основные законы алгебры логики.
- •5. Алгебра Буля. Основные законы
- •6. Булевы функции
- •7. Представление произвольной функции алгебры логики в виде формулы алгебры логики и закон двойственности
- •8. Представление булевых функций нормальными формами
- •8.1. Дизъюнктивная нормальная форма и совершенная дизъюнктивная нормальная форма
- •8.2. Конъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма
- •9. Проблема разрешимости
- •Элементы математической логики
- •1. Предмет математической логики
- •2. Понятие о высказывании
- •3. Основные логические операции
- •4. Равносильность высказываний.
- •1. Основные равносильности:
- •2. Равносильности, выражающие одни логические операции через другие.
- •3. Равносильности, выражающие основные законы алгебры логики.
- •5. Алгебра Буля. Основные законы.
- •6. Булевы функции
- •7. Представление производной функции алгебры логики в виде формулы алгебры логики и закон двойственности
- •8. Представления булевых функций нормальными формами
- •8.1. Дизъюнктивная нормальная форма и совершенная дизъюнктивная нормальная форма
- •8.2. Конъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма
- •9. Проблема разрешимости
- •10. Логика предикатов
- •11. Формулы логики предикат
- •12. Общезначимость и выполнимость формул. Предваренная нормальная форма.
- •Контрольные задания
- •Пример выполнения контрольного Задания
Контрольные задания
1 – 10. Исходя из определений равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграммы Эблера-Венна.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
10.
![]()
11 – 20. Исходя из свойств сочетаний, вычислить сумму и проверить справедливость полученного равенства при n=3.4.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
21 – 30. Задана симметрическая матрица A неотрицательных целых чисел.
1.
Нарисовать на плоскости граф G=(X,U)
(единственный с точностью до изоморфизма),
имеющий заданную матрицу А своей матрицей
смежности. Найти матрицу инцидентности
![]()
графа G.
2.
Нарисовать на плоскости орграф G=(X,U)
(единственный с точностью до изоморфизма)?
Имеющий заданную матрицу А своей матрицей
смежности. Найти матриц инцидентности
![]()
Орграфа G.
21.
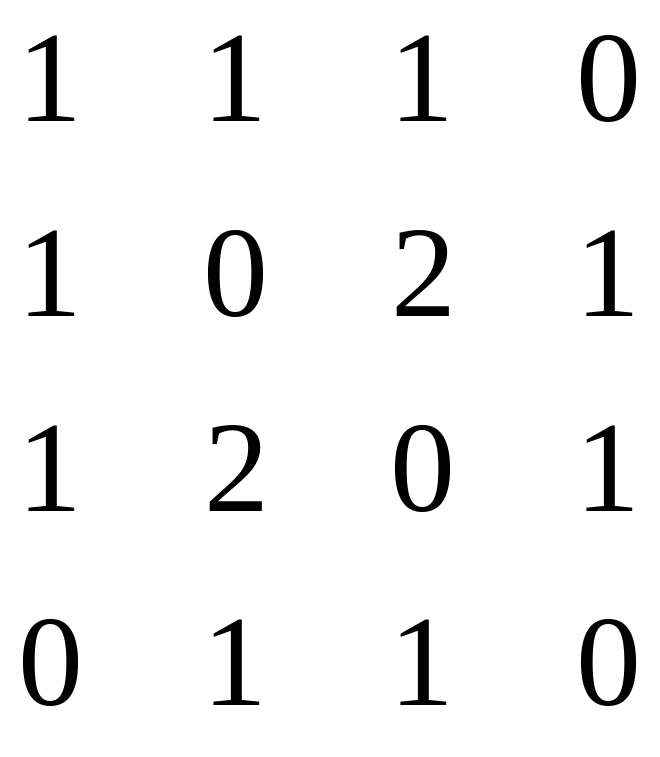 22.
22.
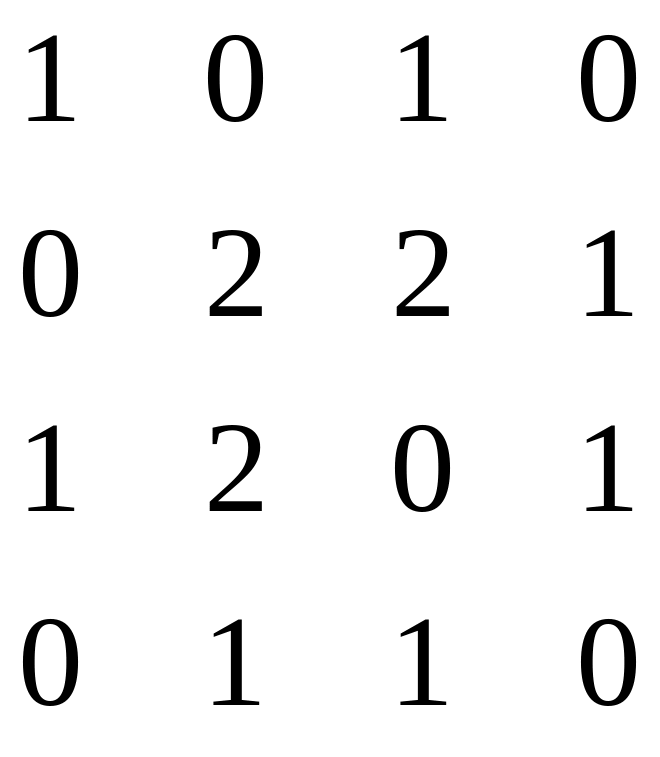
23.
 24.
24.

![]()
25.
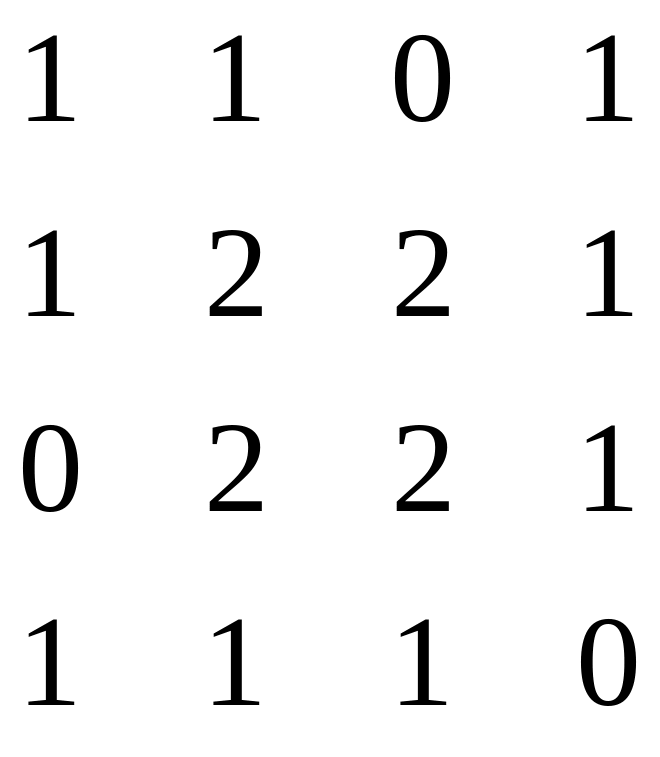 26.
26.
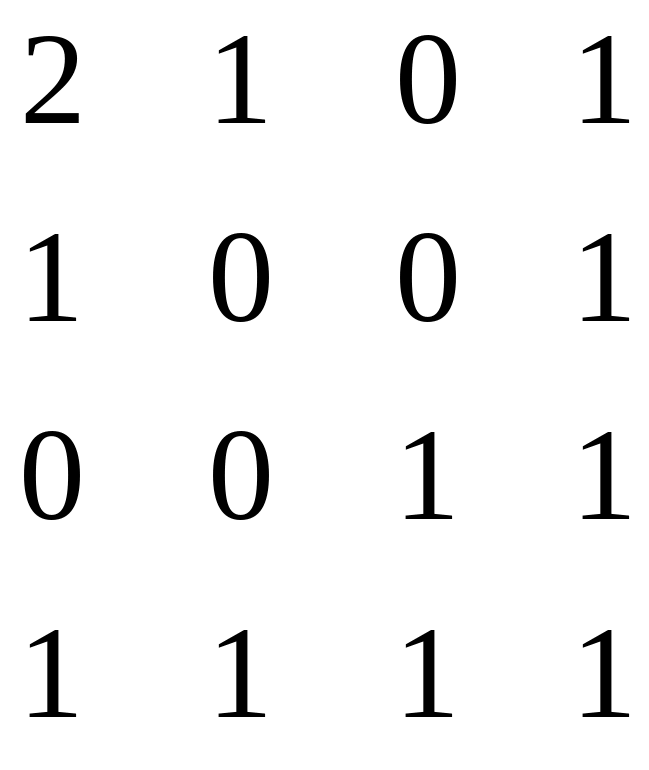
27.
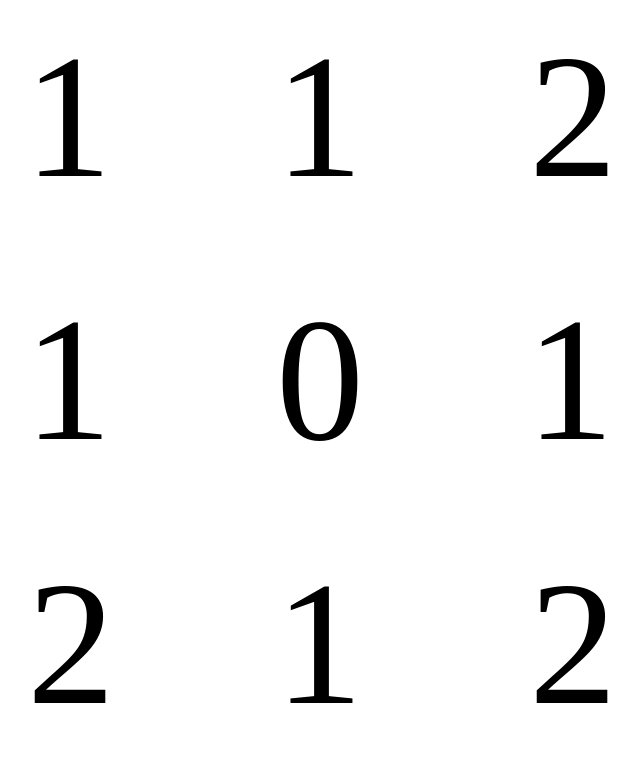 28.
28.
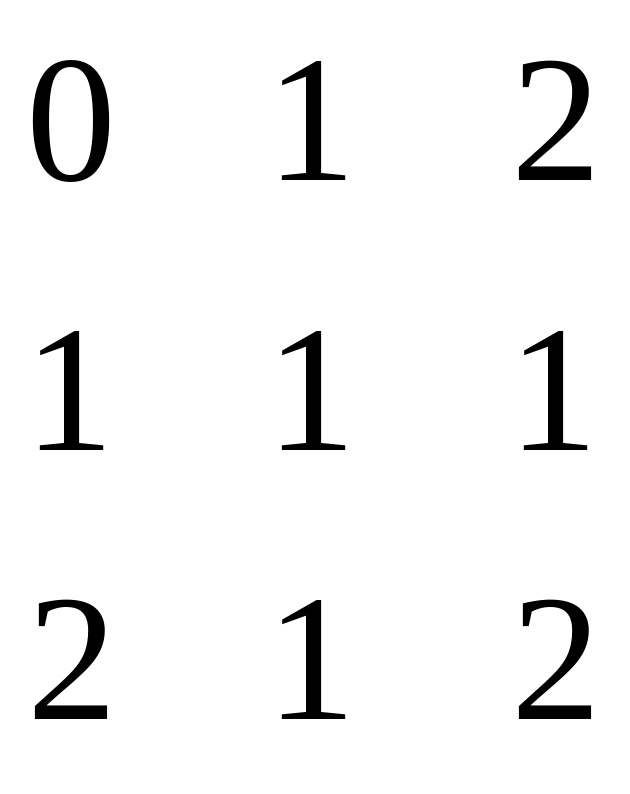
29.
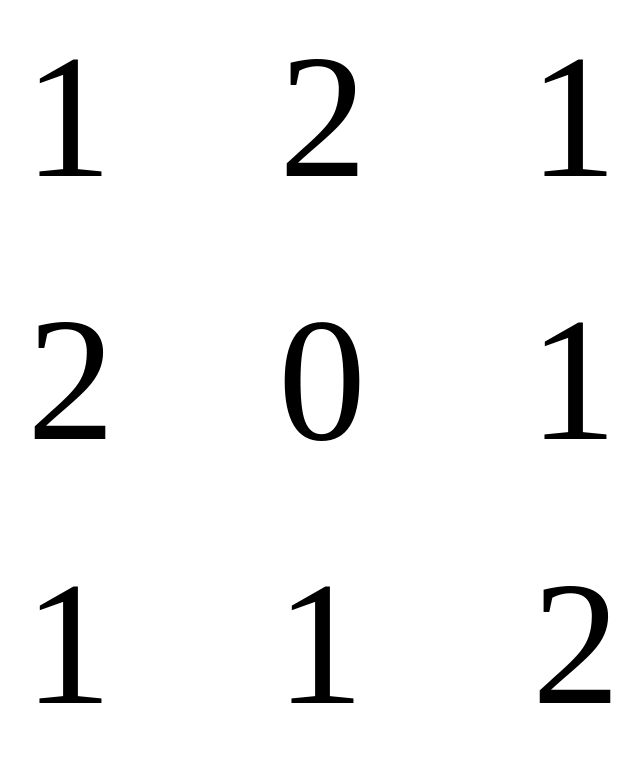 30.
30.
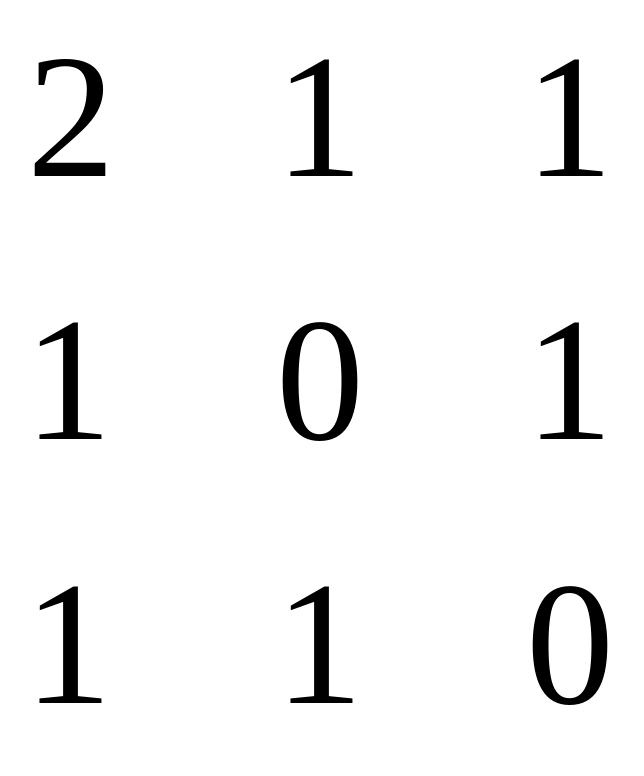
31 – 40. Задана формула φ. От формулы φ перейти к эквивалентной ей формуле ψ так, чтобы формула φ не совершала связок «→» и «↔». Исходя из истинностных таблиц, доказать, что формулы φ и ψ равносильны (логически эквивалентны). Для формулы φ найти СКНФ и СДНФ.
41.
![]() 42.
42.
![]()
43.
![]() 44.
44.
![]()
45.
![]() 46.
46.
![]()
47.
![]() 48.
48.
![]()
49.
![]() 50.
50.
![]()
Пример выполнения контрольного Задания
Исходя из определений равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграммы Эйлера-Венна
Решение. Для удобства введем обозначения:
![]()
![]() ,
,
![]()
![]()
Множества равны,
если они состоят из одних и тех же
элементов. Следовательно, чтобы доказать
тождество
![]() ,
надо показать, что каждый элемент
,
надо показать, что каждый элемент
![]() является элементом множества
и наоборот.
является элементом множества
и наоборот.
Пусть
![]() .
Это означает, что либо
,
либо
.
Это означает, что либо
,
либо
![]() ( по определению объединения множеств
). Если
,
то
( по определению объединения множеств
). Если
,
то
![]() и
и
![]() ,
а это значит , что
,
а это значит , что
![]() .
.
Если
,
то, по определению пересечения множеств,
![]() и
и
![]() .
Если
,
то
;
если
,
то
.
Значит
и
.
Следовательно
.
Если
,
то
;
если
,
то
.
Значит
и
.
Следовательно
Итак,
если
,
то
![]() ,
то есть
,
то есть
![]() .
.
Теперь покажем обратное. Пусть . Тогда, по определению пересечения множеств, и . По определению объединения множеств получаем: , либо и , либо .
Итак
могут представиться следующие случаи:
1)
![]() и
2)
и
и
2)
и
![]() 3)
3)
![]() и
4)
и
.
и
4)
и
.
В случаях 1), 2), 3) , откуда следует, что
![]() .
.
В
случае 4)
и
,
следовательно
![]() ,
а отсюда вытекает, что
,
а отсюда вытекает, что
Таким образом,
если
![]() ,
то
,
то
![]() ,
то есть
,
то есть
![]() .
.
Так как
![]() и
,
то
и
,
то
![]() .
.
Тождество доказано.
Приведенные рассуждения можно представить в виде схемы:
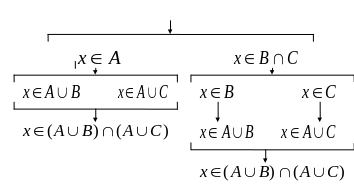
Т.е.
![]()

![]()


и

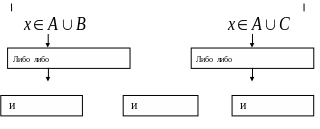



и
Т.е.
Проверим тождество при помощи диаграммы Эйлера-Венна.
Известно, что любое множество можно изобразить графически при помощи диаграммы Венна (Эйлера-Венна). Для этого рисуют либо замкнутую кривую, либо замкнутую ломанную линию и сжимают, что область, ограниченная этими линиями, изображает рассматриваемое множество. В нашем примере на рис. 1и 2 универсальное множество U изображено в виде прямоугольника, а его подмножества A, B, C изображены овалами, ограниченными замкнутыми линиями.
Рассматриваемые множества на диаграммах изображены двойной штриховкой. Множества A, B, C надо стараться располагать одинаково на обеих диаграммах. Выделенные множества представляют одну и ту же часть универсального множества. Это и доказывает тождество.
2. Исходя из свойств сочетаний вычислить сумму:
![]() ,
(1)
,
(1)
![]() ,
,
или
![]() ,
(2)
,
(2)
![]() ,
(3)
,
(3)
Все последующие преобразования будут даны с пояснениями.
![]()
Здесь использована формула определения числа сечения
![]()
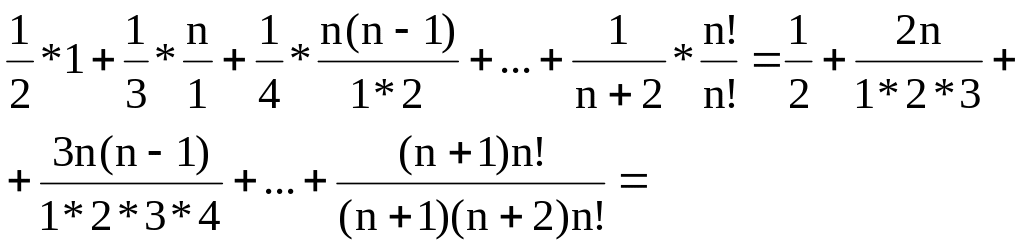
В правой части знаменатели доведены до полных факториалов, а числители, для сохранения равнозначности преобразований, умножены на соответствующие величины.
Таким образом,
![]()
При n=6 имеем
 ,
,
![]()
Итак
![]() .
.
3. Задана симметрическая матрица А неотрицательных целых чисел.
1.
Нарисовать на плоскости граф
![]() (единственный
с точностью до изоморфа), имеющий заданную
матрицу А своей матрицей смежности.
Найти матрицу инцидентности
(единственный
с точностью до изоморфа), имеющий заданную
матрицу А своей матрицей смежности.
Найти матрицу инцидентности
![]() графа G.
графа G.
2.
Нарисовать на плоскости орграф
(единственный с точностью до изоморфизма),
имеющий заданную матрицу А свое матрицей
смежности. Найти матрицу инцидентности
![]() орграфа G.
орграфа G.
А=
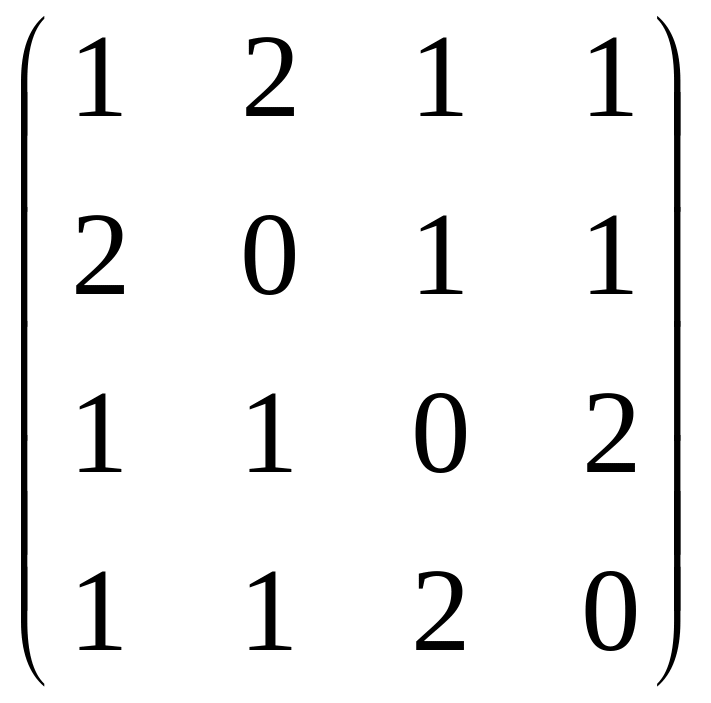
Решение1.
Напомним, что матрицей смежности графа
с множеством вершин
![]() называется матрица
называется матрица
![]() размера
размера
![]() ,
в которой элемент
,
в которой элемент
![]() равен числу ребер в G,
соединяющих
равен числу ребер в G,
соединяющих
![]() с
с
![]() .
Матрица смежности графа G
является симметрической, то есть
.
Матрица смежности графа G
является симметрической, то есть
= .
Построим граф по заданной матрице смежности.
Поскольку
данная матрица является симметрической
матрицей четвертого порядка с
неотрицательными элементами, то ей
соответствует неориентированный граф
с четырьмя вершинами. Расположив вершины
![]() на плоскости произвольным образом
(рис. 3), соединяем их с учетом кратности
ребер.
на плоскости произвольным образом
(рис. 3), соединяем их с учетом кратности
ребер.
А=![]()