8. Представление булевых функций нормальными формами

8.1. Дизъюнктивная нормальная форма и совершенная дизъюнктивная нормальная форма

Определение 1. Элементарной конъюнкцией n переменных называется конъюнкция переменных или их отрицаний.

Элементарная конъюнкция n переменных может быть записана в виде

где

Определение 2. Дизъюнктивной нормальной формой (ДНФ) формулы А называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций.

Для любой формулы алгебры логики путем равносильных преобразований можно получить ее ДНФ, причем не единственную.

Например, для формулы имеем

Среди многочисленных ДНФ А существует единственная ДНФ А, для которой выполняются перечисленные выше (п.7) четыре свойства совершенства.

Такая ДНФ А называется совершенной дизъюнктивной формулой формулы А (СДНФ А).

СДНФ А может быть получен как с помощью таблицы истинности, так и с помощью способа, основанного на равносильных преобразованиях формулы, суть которого состоит в следующем:

1. Путем равносильных преобразований формулы А получают одну из ДНФ А.

2. Если в полученной ДНФ А входящая в нее элементарная конъюнкция В не содержит переменную , то, используя равносильность

элементарную конъюнкцию В заменяют на две элементарных конъюнкции , каждая из которых содержит переменную .

3. Если в ДНФ А входят две одинаковых элементарных конъюнкции В, то лишнюю можно отбросить, пользуясь равносильностью

4. Если некоторая элементарная конъюнкция В, входящая в ДНФ А, содержит переменную и ее отрицание , то B ~ 0, и В можно исключить из ДНФ А, как нулевой член дизъюнкции.

5. Если некоторая элементарная конъюнкция, входящая в ДНФ А, содержит переменную дважды, то одну переменную можно отбросить, пользуясь равносильностью ~ .

После выполнения описанной процедуры будет получена СДНФ А.

Пример. ДНФ .

Решение. Так как элементарная конъюнкция B ~ x, входящая в ДНФ А, не содержит переменной у, то, пользуясь равносильностью

заменим ее на две элементарных конъюнкции и . В результате получим

ДНФ

Так как теперь ДНФ А содержит две одинаковых элементарных конъюнкции , то лишнюю отбросим, пользуясь равносильностью

В результате получим

Так как элементарная конъюнкция содержит переменную y и ее отрицание , то ~ 0, и ее можно отбросить как нулевой член дизъюнкции.

Таким образом, получаем

8.2. Конъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма

Определение 1. Элементарной дизъюнкцией n переменных называется дизъюнкция переменных или их отрицаний.

Элементарная дизъюнкция n переменных может быть записана в виде

где

Определение 2. Конъюнктивной нормальной формой (КНФ) формулы А называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.

Для любой формулы алгебры логики путем равносильных преобразований можно получить ее КНФ, причем не единственную.

Например, для формулы имеем

то есть

КНФ

Но так как

то

КНФ

А так как

то

КНФ

Определение 3. КНФ А называется совершенной конъюнктивной нормальной формой формулы А ( СКНФ А ), если для нее выполнены условия:

1. Все элементарные дизъюнкции, входящие в КНФ А, различны.

2. Все элементарные дизъюнкции, входящие в КНФ А, содержат все переменные.

3. Каждая элементарная дизъюнкция, входящая в КНФ А, не содержит двух одинаковых переменных.

4. Каждая элементарная дизъюнкция, входящая в КНФ А, не содержит переменную и ее отрицание.

Каждая не тождественно истинная формула имеет единственную СКНФ.

Один из способов получения СКНФ состоит в использовании таблицы истинности для формулы .

Другой способ получения СКНФ, использующий равносильные преобразования, состоит в следующем:

1. Путем равносильных преобразований формулы А получают одну из КНФ А.

2. Если в полученной КНФ А входящая в нее элементарная дизъюнкция В не содержит переменную , то, используя равносильность

элементарную дизъюнкцию В заменяют на две элементарные дизъюнкции и , каждая из которых содержит переменную .

3. Если в КНФ А входят две одинаковых элементарных дизъюнкции В, то лишнюю можно отбросить, пользуясь равносильностью

4. Если некоторая элементарная дизъюнкция, входящая в КНФ А, содержит переменную дважды, то лишнюю можно отбросить, пользуясь равносильностью

5. Если некоторая элементарная дизъюнкция, входящая в КНФ А, содержит переменную 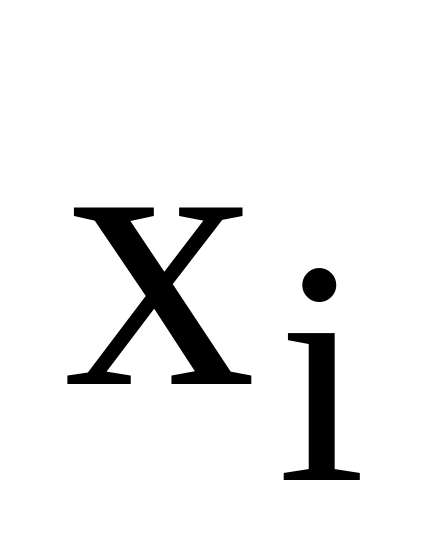и ее отрицание, то и, следовательно, вся элементарная дизъюнкция имеет значение 1, а поэтому ее можно отбросить, как единственный член конъюнкции.

После описанной процедуры будет получена СКНФ А.

Например, для формулы КНФ

Так как обе элементарная дизъюнкции различны и содержат все переменные ( х и у ), то первое и второе условия СКНФ А выполнены.

Элементарная дизъюнкция содержит переменную х дважды, но , и поэтому КНФ Причем ни одна из элементарных дизъюнкций не содержит переменную и ее отрицание. Значит, теперь выполнены все условия СКНФ А, и, следовательно,

СКНФ

Пример. Построить СДНФ и СКНФ для формулы

.

Решение. Напомним, что для решения необходимо четко знать определения КНФ, ДНФ, СКНФ, СДНФ и алгоритмы построения СКНФ и СДНФ. Составим истинную таблицу для формулы (табл. 18)

Таблица 18

p	q
1	1	0	0	1	0
1	0	1	1	1	1
0	1	0	1	1	1
0	0	1	1	0	0

В первых двух столбцах таблицы выписаны всевозможные соединения из 1 и 0 ( всевозможные интерпретации ). Таких соединений будет поэтому истинная таблица содержит 5 строк ( 1 строка содержит буквы, входящие в , части формулы и саму формулу ). При заполнении столбцов 3 – 5 использованы только определения операций отрицания ( 3 – й столбец ), импликации ( 4 – й столбец ), дизъюнкция ( 5 – й столбец ), конъюнкция ( 6 столбец ).

Построим СДНФ для . В истинной таблице отметим строки, где принимает значение 1 ( 3 и 4 строки ). В 3 – й строке =1, если p=1, а q=0. Составляем конъюнкцию . В 4 – й строке p=0, а q=1, следовательно, этой строке соответствует конъюнкция Теперь полученные конъюнкции соединим связкой дизъюнкции и получаем СДНФ для формулы

Теперь составим СКНФ для . Отметим строки, в которых принимает значение 0. Такими строками являются 2 и 5. Составляем дизъюнкцию ( 2 – я строка ) и ( 5-я строка ). Соединим дизъюнкции в конъюнкцию и получим СКНФ

Проверим эквивалентность и , и . Для этого составим истинностные таблицы ( табл. 19 )

Таблица 19

p	q
1	1	0	0	0	0	0	1	0	0	0
1	0	0	1	1	0	1	1	1	1	1
0	1	1	0	0	1	1	1	1	1	1
0	0	1	1	0	0	0	0	1	0	0

В 7, 10 и 11 столбцах помещены значения , и соответственно. Эти столбцы одинаковы, следовательно, формулы и , и эквивалентны. Из таблицы видно, что формулы и также эквивалентны.