Глава 3. Уравнение с одним неизвестным и методы его численного решения

В данной главе рассмотрены некоторые методы численного решения нелинейных уравнений. Пусть дано уравнение

, (3.1)

где функция определена и непрерывна на некотором конечном или бесконечном интервале . Всякое значение , обращающее функцию в нуль, называется корнем уравнения (3.1). Мы будем предполагать, что уравнение (3.1) имеет лишь изолированные корни, т.е. для каждого корня уравнения (3.1) существует окрестность, не содержащая других корней уравнения (3.1). В дальнейших методах мы считаем, что нахождение корня происходит именно в такой окрестности.

0. Метод дихотомии

В данном разделе мы рассмотрим метод дихотомии (половинного деления) уточнения корня уравнения (3.1). Пусть дано уравнение (3.1), где функция непрерывна на отрезке и . Для нахождения коря уравнения (3.1), принадлежащего отрезку , делим этот отрезок пополам. Если , то является корнем уравнения (3.1). Если 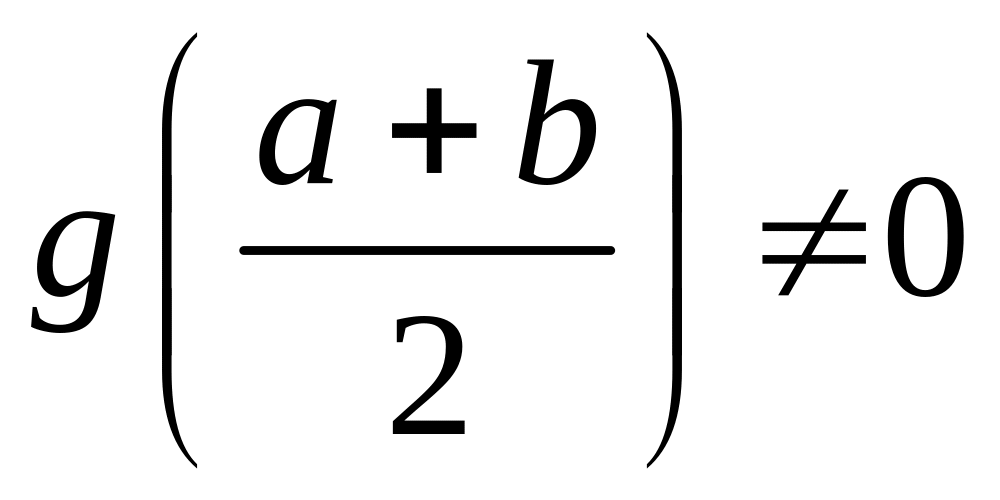, то выбираем ту из половин , на концах которой функция имеет противоположные знаки. Новый суженный отрезок снова делим пополам и проводим то же рассмотрение и т.д. В результате получаем на некотором этапе либо точный корень уравнения (3.1) или же бесконечную последовательность вложенных друг в друга отрезков

таких, что

. (3.2)

Так как левые концы образуют монотонную неубывающую ограниченную последовательность, а правые концы - монотонную невозрастающую ограниченную последовательность, то существуют пределы

.

В силу (3.2), и следующего неравенства:

,

мы получаем . Итак, . Переходя к пределу в неравенстве (3.2) и, учитывая непрерывность функции , получаем

.

Таким образом, число является корнем уравнения (3.1), причем, очевидно,

.

Полученное неравенство можно использовать для оценки погрешности найденного приближения. Так, если требуется найти решение уравнения с точностью , то процесс деления отрезка заканчиваем, когда выполняется неравенство . В качестве приближенного значения корня можно взять .

3.2. Метод простой итерации решения одного нелинейного уравнения с одним неизвестным

Преобразуем уравнение (3.1) к виду

, (3.3)

где . Предположим, что функция удовлетворяет следующим условиям:

• ,

• для любого выполняется ,

• .

В этом случае уравнение (3.1) имеет один единственный корень. Действительно, в силу теоремы Лагранжа,

.

Поэтому отображение является сжатым отображением полного метрического пространства в себя. По теореме С. Банаха, такое отображение имеет единственную неподвижную точку, значит, уравнение (3.1) имеет единственный корень . Пусть - произвольная точка. Тогда последовательность точек

сходится к точке . Кроме того, имеет место оценка погрешности:

.

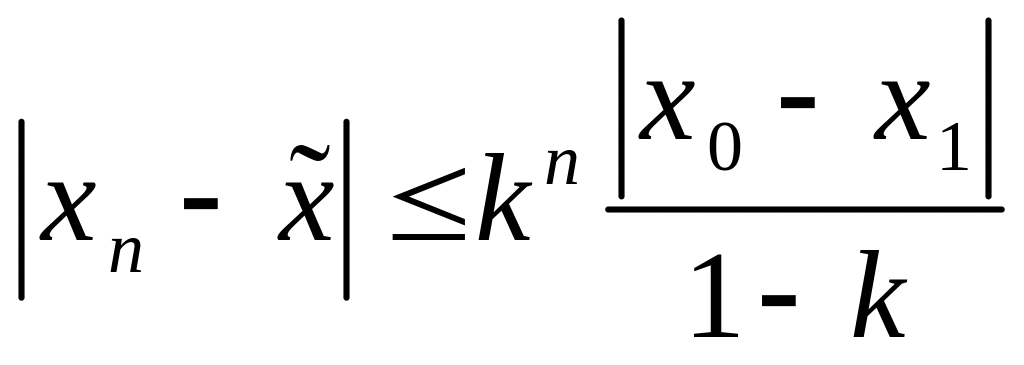Итак, для решения уравнения (3.1) выбирается некоторое начальное приближение и последовательно находятся приближенные решения (итерации) уравнения (3.1). Значение итерации выражается через известную предыдущую итерацию. Данный метод носит название метода итераций.