ГОСУДАРСТВЕННЫЙ КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ

ПО ВЫСШЕМУ ОБРАЗОВАНИЮ

_______________

МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(государственный технический университет)

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ

Методические указания к выполнению лабораторных работ в среде MathCad

Москва

Издательство МАИ

2009

Приводится описание лабораторных работ, выполняемых в среде MathCad. Рассматривается применение z-преобразования к решению разностных уравнений и систем уравнений. Кроме того, рассмотрены численные методы решения алгебраических уравнений и систем.

Предназначено для студентов факультета «Системы управления информатики и электроэнергетики».

© Московский авиационный институт, 2009

Предисловие

Настоящее пособие содержит общие теоретические сведения по z – преобразованию, которое называется также преобразованием Лорана и применению его к решению разностных уравнений и систем уравнений. Изложению этих теоретических сведений посвящена первая глава. Во второй главе формулируются варианты домашнего вычислительного задания, приводятся примеры решения разностных уравнений и систем, а также рассматриваются примеры решения этих уравнений в среде MathCad. Третья глава посвящена описанию численных методов решения алгебраических уравнений с одним неизвестным. В четвертой главе приводятся некоторые методы численного решения систем алгебраических уравнений.

Глава 1. Z – преобразование и его применение

В этой главе дается понятие z – преобразования, которое называется также преобразованием Лорана, и рассматриваются его свойства.

1.1. Преобразование Лорана и его свойства

Пусть задана последовательность комплексных чисел, удовлетворяющая условию:

, для некоторых чисел . (1.1)

Такую последовательность будем называть последовательностью-оригиналом.

Изображением по Лорану (z-преобразованием), соответствующим оригиналу , называется функция комплексного переменного

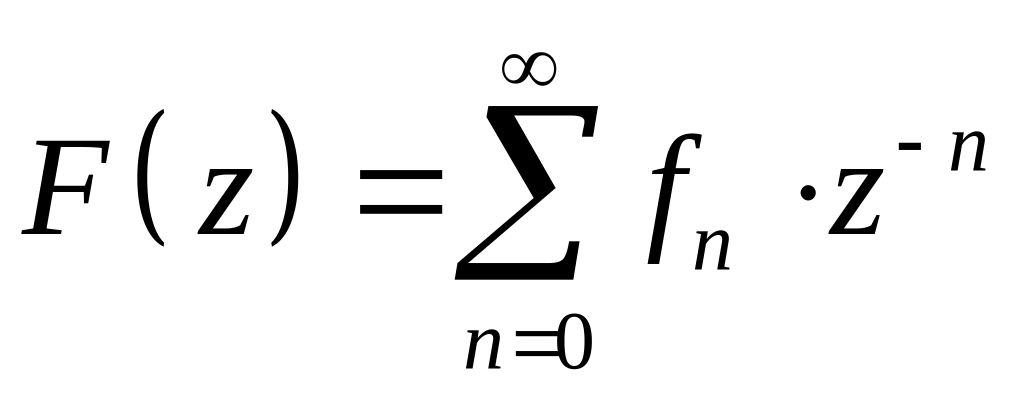. (1.2)

Соответствие между оригиналом и изображением будем обозначать знаком . При выполнении условия (1.1) последовательности соответствует функция аналитическая во внешности круга . Обратно, каждая такая функция однозначно определяет последовательность , которую можно найти одним из следующих способов.

1. Так как правую часть (1.2) можно рассматривать как ряд Лорана функции , то по формуле для коэффициентов ряда Лорана, находим

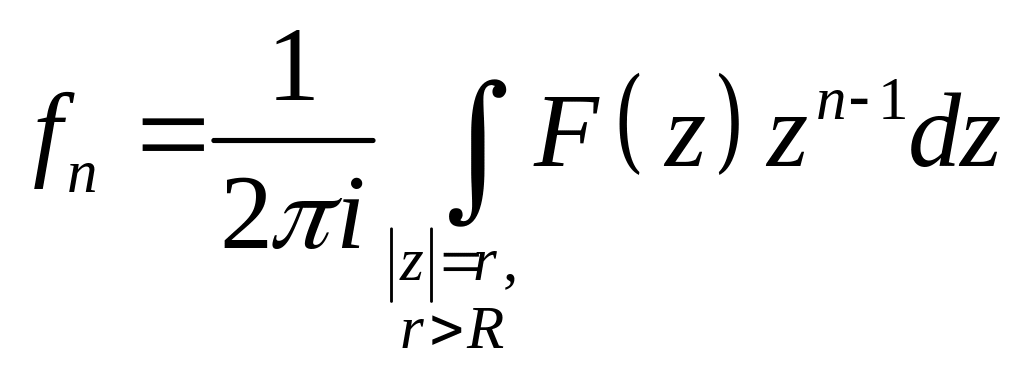. (1.3)

2. Так как ряд представляет собой ряд Тейлора функции 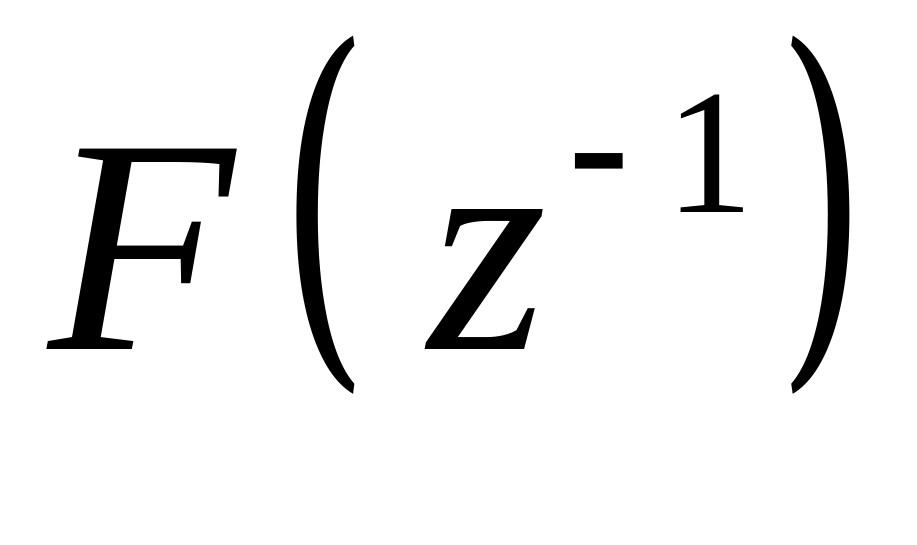, то согласно формуле для коэффициентов ряда Тейлора, находим

.

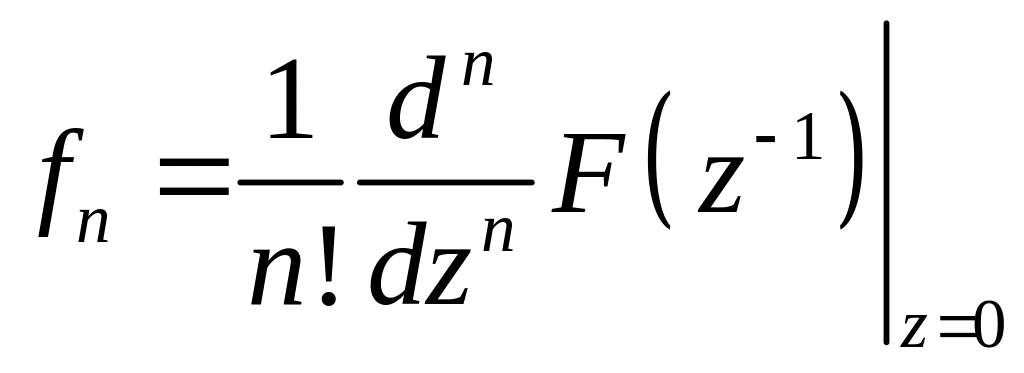3. Согласно основной теореме теории вычетов, из формулы (1.3) следует

,

где сумма распространяется на все особые точки функции .

При применении z-преобразования, важно знать, какие операции над изображениями соответствую определенным действиям над последовательностями-оригиналами и наоборот.

Теорема 1.1 (теорема линейности). Пусть - оригиналы, а - их изображения. Тогда

.

Теорема 1.2 (теорема опережения). Если , то

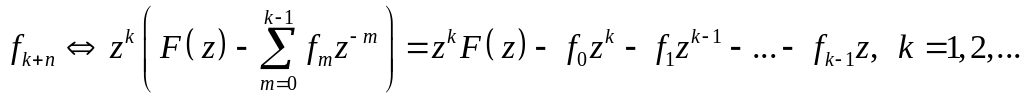
Доказательство. По определению z-преобразования, имеем

.

Теорема доказана.

Теорема 1.3 (теорема о свертке). Если - оригиналы, а - их изображения, то

.

Доказательство. Перемножая и , получаем

.

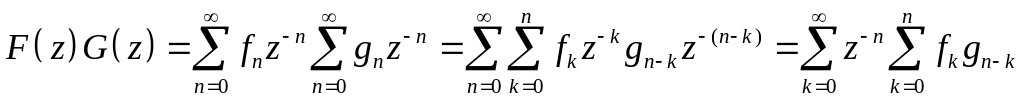Теорема доказана.

Теорема 1.4 (дифференцирование изображения). Пусть . Тогда

.

В следующей таблице приведены некоторые последовательности-оригиналы и их изображения.

Таблица 1.1. Соответствия при z-преобразовании

№
1
2
3
4

Пример. Найти z-преобразование последовательности-оригинала .

Решение. По формуле Эйлера имеем

.
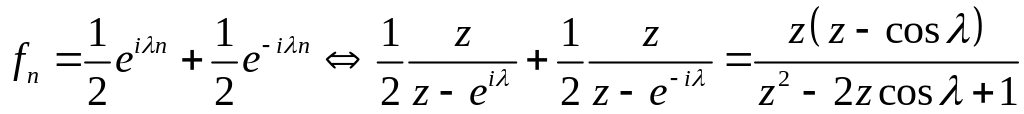