Лекция 5

§13 Функция распределения

Во всех рассмотренных выше случаях случайная величина определялась путем задания значений самой величины и вероятностей этих значений. Однако такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально. Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.

Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. Х < x, обозначим через F(x).

Определение. Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина примет значение, меньшее х:

F (x) = p (X < x). (*)

Функцию распределения также называют интегральной функцией. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.

Свойства функции распределения

Свойство 1. Значения функции распределения принадлежат отрезку [0;1], то есть 0 ≤ F(x) ≤ 1.

Свойство 2. Функция распределения является неубывающей функцией, то есть F(x₂) ≥ F(x₁) при х₂ > x₁.

Свойство 3. Если все возможные значения Х лежат на интервале (a, b), то F(x) = 0 при и F(x) = 1 при .

Свойство 4. Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) , равна разности значений функции распределения на концах интервале: .

Свойство 5. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:

Для дискретной случайной величины значение F(x) в каждой точке представляет собой сумму вероятностей тех ее возможных значений, которые меньше аргумента функции.

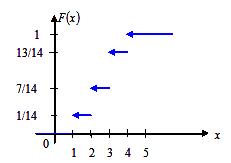
График функции F(x) представляет собой ступенчатую линию. Скачки функции F(x) в точках х = х₁, х₂ …, где (x₁<x₂<…) равны соответствующим вероятностям р₁, p₂, ….

Задача. В партии из 8 деталей имеется 5 стандартных (3 нестандартных). На удачу выбираются 4 детали. Случайная величина X – это число стандартных деталей среди выбранных. Найти функцию распределения дискретной случайной величины, и построить график функции распределения этой случайной величины.

Решение. Очевидно, что Х может принимать 4 значения: 1, 2, 3, 4, то есть X = 1, 2, 3, 4. Используем классическое определение вероятности и правило произведения событий: где n – число всех равновозможных элементарных исходов, которые можно выбрать способами; m – число элементарных исходов, благоприятных осуществлению события.

Найдем вероятность принятия величиной X всех ее значений.

Для число всех благоприятных исходов равно , так как извлечь 1 стандартную деталь из 5 стандартных в партии можно способами. Извлечь 3 нестандартных детали из 3-х нестандартных в партии можно способами. Так как эти события должны выполнятся одновременно, то число будет равно их произведению , то есть