§27 Эмпирическая функция распределения

Пусть известно статистическое распределение (или статистический ряд) количественного признака ; – число наблюдений, при которых наблюдалось значение признака, меньшее , т.е. ; – общее число наблюдений (объём выборки). Тогда относительная частота события есть . При изменении меняется и , т.е. относительная частота является функцией x. Так как эта функция находится эмпирическим (т.е. опытным) путём, то её называют эмпирической.

Определение. Эмпирической функцией распределения (функцией распределения выборки) называется функция (1), определяющая для каждого значения x относительную частоту события . В (1) – число вариант, меньших x ( , - варианты, – объём выборки). Поэтому для расчетов удобна формула вида:

.

Тогда, например, означает , где число вариант, меньших или в табличной форме:

Функцию распределения генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями распределения состоит в том, что определяет вероятность события , а относительную частоту того же события. обладает всеми свойствами .

Свойства эмпирической функции распределения :

Свойство 1. Значения принадлежат ; ;

Свойство 2. неубывающая функция;

Свойство 3. Если наименьшая варианта, а наибольшая варианта, то для , для ;

Свойство 4. непрерывная слева функция.

Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Пример. Построить эмпирическую функцию распределения по данному распределению выборки

Варианты	2	6	10
Частоты	12	18	30

Решение. Здесь – наименьшая варианта, следовательно, для ;

– наибольшая варианта, тогда при .

Для имеем , а для следует .

Приведем аналитический вид полученной эмпирической функции распределения , ее график и полигон:

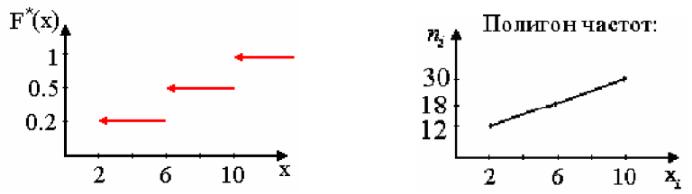
Полигон относительных частот имеет вид

где координаты его вершин определяются по формулам , , , .

§28 Выборочные характеристики случайной величины

Определение. Пусть производится измерений случайной величины, в результате которых получены значения .

Выборочным средним называют число .

Выборочной дисперсией называется число, которое находится по формуле: .

Исправленной (или улучшенной) выборочной дисперсией называется число , тогда .

Выборочным средним квадратическим отклонением называется число . Исправленным (или улучшенным) выборочным средним квадратическим отклонением называется число .

Если случайная величина задается таблицей частот , то выборочные характеристики удобно считать по формулам:

1. , где .

2. .

3. 

4. ,

где частоты, – относительные частоты.

Пример. Пусть случайная величина задана таблицей относительных частот:

	0	1	2
	0,3	0,2	0,5

. Найти выборочные характеристики.

Решение. . Так как случайная величина задана таблицей относительных частот, то найдем выборочные характеристики (выборочное среднее и выборочную дисперсию), используя формулы 3 и 4:

.

Улучшенную выборочную дисперсию, выборочное среднее квадратическое отклонение и улучшенное выборочное среднее квадратичное отклонение найдем по формулам из вышесказанного определения:

.

.

.