Лекция 9

§26 Интервальные таблицы частот

При большом объеме выборки ее элементы объединяют в группы (разряды, интервалы), представляя результаты опытов в виде интервального статистического ряда. Для этого весь диапазон значений случайной величины (от до ) разбивают на k интервалов одинаковой длины (обычно k меняется от 5 до 20) и подсчитывают частоты (или относительные частоты ) значений выборки, попавших в интервалы. Величина называется плотностью частоты, а – плотностью относительной частоты.

Пусть – середина -го интервала, – число элементов выборки, попавших в -й интервал (при этом элемент, совпавший с верхней границей интервала, относится к последующему интервалу). Таким образом, получим группированный статистический ряд, в верхней строке которого записаны середины соответствующих интервалов , а в нижней – частоты:

			…
			…

Пример 1. Выборка, полученная в результате статистического наблюдения (единицы измерения опускаем) – 3,14; 1,41; 2,87; 3,62; 2,71; 3,95.

Решение. Ранжированный вариационный ряд:

, где

Соответствующее статистическое распределение :

	1-2	2-3	3-4
	1	2	3

Для графического представления интервальных статистических распределений принято использовать гистограмму относительных частот.

Гистограммой относительных частот интервального статистического ряда называется ступенчатая фигура, составленная из прямоугольников, построенных на интервалах группировки длины и высоты так, что площадь каждого прямоугольника равна относительной частоте .

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки длиной параллельно оси ординат. Очевидно, площадь -го частичного прямоугольника равна – относительной частоте вариант, попавших в -ый интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот (т.е. равна 1), а площадь гистограммы частот равна объему выборки .

Пример 2. Имеется распределение 80 предприятий по числу работающих на них человек:

	150	250	350	450	550	650	750
	1	3	7	30	19	15	5

Решение. Признак Х – число работающих (чел.) на предприятии. В данной задаче признак Х является дискретным. Поскольку различных значений признака сравнительно немного – k = 7, применять интервальный ряд для представления статистического распределения нецелесообразно (в прикладной статистике в подобных задачах часто используют именно интервальный ряд). Ряд распределения – дискретный. Построим полигон распределения частот (рис. 1).

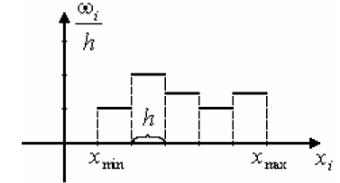
Пример 3. Дано распределение 100 рабочих по затратам времени на обработку одной детали (мин):

Решение. Признак Х – затраты времени на обработку одной детали (мин). Признак Х – непрерывный, ряд распределения – интервальный. Построим гистограмму частот (рис. 2), предварительно определив и плотность частоты :