16. Регрессионные модели экспериментов и их статистический анализ.

Пусть выходная переменная y зависит от контролируемых переменных . В результате выполнения n имитационных экспериментов будет получен вектор , который зависит от матрицы

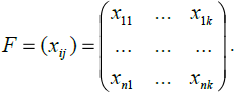
Здесь первый индекс i – номер эксперимента, j – номер переменной, так что

- значение j – й контролируемой переменной в i – м эксперименте.

В теории планирования экспериментов вектор

называется вектором результатов измерения, а матрица F называется

матрицей плана эксперимента.

При постановке экспериментов принимается априори (лат. a priori – из

предшествующего, до опыта) предположение, что зависимость между

выходной и управляемыми переменными имеет вид:

причем функция считается известной с точностью до конечного

числа неизвестных параметров (коэффициентов) . Другими словами, вид функции также задается исследователем априори. Например, эта функция может быть задана в виде полинома, тригонометрической функции и т.п.

Из-за погрешностей эксперимента, влияния случайных факторов,

вектор результатов измерений и матрица плана F

связаны не точной зависимостью, а стохастической зависимостью

где - измеренная в i-м эксперименте величина y (выходной сигнал), - случайная ошибка «измерений» этой величины в i-м эксперименте,

.

Следуя основам теории измерений, примем предположение о том, что

случайные ошибки распределены по нормальному закону, то есть плотность

вероятности распределения случайной величины x есть

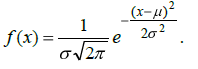
Это предположение называют также основной гипотезой теории измерений. Принятие этого предположения означает, что средние значения ошибок, т. е. математическое ожидание случайной ошибки измерений , равно нулю ( ошибки в разных опытах некоррелированы ( и дисперсия где - стандартное отклонение (разброс) случайной величины.

Учитывая, что выражение запишем в виде:

В теории планирования эксперимента функция

называется поверхностью (имеется в виду еѐ графическое изображение)

отклика или функцией регрессии.

Задача регрессионного анализа заключается в том, чтобы оценить

значения по выборке экспериментальных значений

. Наиболее изученным в теории планирования

экспериментов является случай, когда функция линейна по параметрам

В этом случае зависимость имеет вид:

Здесь функция рассматривается как заданная векторная непрерывная функция своих аргументов.

Наконец, частным случаем зависимости является случай, когда

выходной сигнал y линейно зависит не только от коэффициентов

(параметров) но и контролируемые переменные также

линейно входят в правую часть. Тогда выражения преобразуется к

виду:

В матричной форме записи это уравнение имеет вид:

Здесь F - матрица размером n m (k- количество

параметров).

Теперь рассмотрим линейные оценки значений параметров которые получаются на основе экспериментов и имеют

вид:

где T – матрица размера m n.

Оценка называется наилучшей линейной несмещенной оценкой,

если она имеет наименьшие дисперсии среди всех оценок.